Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số, tài liệu bao gồm 89 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu bao gồm các nội dung sau:

Bài 1. Sự đồng biến, nghịch biến của hàm số

Bài 2. Cực trị của hàm số

Bài 3. Giá trị lón nhất và giá trị nhỏ nhất của hàm số

Bài 4. Đường tiệm cận

Bài 5. Khảo sát sự biến thiên và vẽ đồ thị hàm số

Bài 6. Bài toán thường gặp về đồ thị hàm số

Ôn tập chương I

Câu hỏi trong kì thi THPTQG

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số - có đáp án

Chương I

Ứng dụng đạo hàm để khảo sát và vẽ đô thị của hàm số

§1. Sự đồng biến, nghịch biến của hàm số

A. Kiến thức cần nắm

1. Bảng đạo hàm

- Hàm số sơ cấp

\({(C)^\prime } = 0\)

\({(x)^\prime } = 1,{(kx)^\prime } = k{x^\prime } = k\)

\({\left( {{x^{\prime \prime }}} \right)^\prime } = n{x^{n - 1}},n \in \mathbb{N},n > 1\)

\({(\sqrt x )^\prime } = \frac{1}{{2\sqrt x }},x > 0\)

\({\left( {\frac{1}{x}} \right)^\prime } =  - \frac{1}{{{x^2}}},x \ne 0\)

\({(\sin x)^\prime } = \cos x\)

\({(\cos x)^\prime } =  - \sin x\)

\({(\tan x)^\prime } = \frac{1}{{{{\cos }^2}x}} = 1 + {\tan ^2}x\)

\({(\cot x)^\prime } = \frac{{ - 1}}{{{{\sin }^2}x}} =  - \left( {1 + {{\cot }^2}x} \right)\)

\({\left( {{a^x}} \right)^\prime } = {a^x}\ln a,0 < a \ne 1\)

\({\left( {{e^x}} \right)^\prime } = {e^x}\)

\[\begin{array}{*{20}{c}}{\left( {{{\log }_a}x} \right) = \frac{1}{{x\ln a}},0\left\langle {a \ne 1,x} \right\rangle 0}\\{(\ln x)' = \frac{1}{x},x > 0}\end{array}\]

- Hàm số hợp

u = u(x)

\({(ku)^\prime } = k{u^\prime }\)

\({\left( {{u^\alpha }} \right)^\prime } = \alpha  \cdot {u^{\alpha  - 1}} \cdot {u^\prime }\)

\({(\sqrt u )^\prime } = \frac{{{u^\prime }}}{{2\sqrt u }}\)

\({\left( {\frac{1}{u}} \right)^\prime } =  - \frac{{{u^\prime }}}{{{u^2}}}\)

\({(\sin u)^\prime } = {u^\prime }\cos u\)

\({(\cos u)^\prime } =  - {u^\prime }\sin u\)

\({(\tan u)^\prime } = \frac{{{u^\prime }}}{{{{\cos }^2}u}} = \left( {1 + {{\tan }^2}u} \right){u^\prime }\)

\({(\cot u)^\prime } = \frac{{ - {u^\prime }}}{{{{\sin }^2}u}} =  - \left( {1 + {{\cot }^2}u} \right){u^\prime }\)

\({\left( {{a^u}} \right)^\prime } = {u^\prime }{a^u}\ln a\)

\({\left( {{e^\prime }} \right)^\prime } = {u^\prime }{e^u}\)

\({\left( {\log {u_a}} \right)^\prime } = \frac{{{u^\prime }}}{{u\ln a}},0 < a \ne 1\)

\({(\ln u)^\prime } = \frac{{{u^\prime }}}{u}\)

- Quy tắc

\(u = u(x),v = v(x)\)

\({(u + v)^\prime } = {u^\prime } + {v^\prime }\)

\({(u - v)^\prime } = {u^\prime } - {v^\prime }\)

\({(uv)^\prime } = {u^\prime }v + u{v^\prime }\)

\({\left( {\frac{u}{v}} \right)^\prime } = \frac{{{u^\prime }v - u{v^\prime }}}{{{v^2}}}\)

\({\left( {\frac{1}{v}} \right)^\prime } =  - \frac{{{v^\prime }}}{{{v^2}}}\)

\({(ax + b)^\prime } = a\)

\({\left( {\frac{{ax + b}}{{cx + d}}} \right)^\prime } = \frac{{ad - bc}}{{{{(cx + d)}^2}}}\)

2. Có các dạng toán co bản:

Dạng 1. Tìm các khoảng đồng biến, nghịch biến của hàm số đã cho

Phương pháp: Áp dụng qui tắc. Xét hàm số y = f(x)

Qui tắc:

(1) Tìm tập xác định

(2) Tính \({y^\prime }\), tìm các nghiệm \({x_i}(i = 1,2,3 \ldots )\) mà tại đó \({y^\prime } = 0\) hoặc \({y^\prime }\) không xác định

(3) Tìm các giới hạn vô cực; các giới hạn \( + \infty , - \infty \) và tại các điểm mà hàm số không xác định (nếu có)

(4) Lập bảng biến thiên

(5) Dựa vào bảng biến thiên, kết luận.

Dạng 2. Tìm tham số \(m \in \mathbb{R}\) để hàm số luôn luôn đồng biến hay nghịch biến trên tập xác định của nó

Phương pháp: Thường cho hàm số bậc ba: \(y = f(x,m)\) chứa biến x và tham số m. Khi tính đạo hàm ta được hàm số bậc hai. Giả sử hàm bậc hai \({y^\prime } = a{x^2} + bx + c\)

Phương pháp: Áp dụng qui tắc:

Qui tắc:

(1) Tìm tập xác định

(2) Tính đạo hàm \({y^\prime }\)

(3) Lập luận: Nếu cơ số \(a\) có chứa tham số

Hàm số đồng biến trên \(\mathbb{R}\) khi và chỉ khi \({y^\prime } \ge 0\); Hàm số nghịch biến trên \(\mathbb{R}\) khi và chỉ khi \({y^\prime } \le 0\)

- Xét \(a = 0 \Rightarrow m\) thay vào đạo hàm. Nhận xét \({y^\prime }\) đưa ra kết luận (1)

- Xét \(a \ne 0,{y^\prime } \ge 0,\forall x \in \mathbb{R} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 0}\\{\Delta  \le 0}\end{array}} \right.\) (2) \(\quad \)

- Xét \(a \ne 0,{y^\prime } \le 0,\forall x \in \mathbb{R} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a < 0}\\{\Delta  \le 0}\end{array}} \right.\) (2')

(4) So với (1) và (2) hoặc (1) và (2') đưa ra kết luận yêu cầu bài toán.

Dạng 3 . Tìm tham số \(m \in \mathbb{R}\) để hàm số luôn luôn đồng biến hay nghịch biến trên khoảng \((\alpha ;\beta )\)

Phương pháp:

a) Hàm số f đồng biến trên \((\alpha ;\beta ) \Leftrightarrow {y^\prime } \ge 0,\forall x \in (\alpha ;\beta )\) và \({y^\prime } = 0\) chỉ xảy ra tại một số hữu hạn điểm thuộc \((\alpha ;\beta )\).

- Nếu bất phương trình \({f^\prime }(x,m) \ge 0 \Leftrightarrow h(m) \ge g(x)(*)\) thì f đồng biến trên \((\alpha ;\beta ) \Leftrightarrow h(m) \ge {\max _{(\alpha ;\beta )}}g(x)\)

- Nếu bất phương trình \({f^\prime }(x,m) \ge 0 \Leftrightarrow h(m) \le g(x)\) (**) thì f đồng biến trên \((\alpha ;\beta ) \Leftrightarrow h(m) \le {\min _{(\alpha ;\beta )}}g(x)\)

b) Hàm số f nghịch biến trên \((\alpha ;\beta ) \Leftrightarrow {y^\prime } \ge 0,\forall x \in (\alpha ;\beta )\) và \({y^\prime } = 0\) chỉ xảy ra tại một số hữu hạn điểm thuộc \((\alpha ;\beta )\).

- Nếu bất phương trình \({f^\prime }(x,m) \le 0 \Leftrightarrow h(m) \ge g(x)(*)\) thì f nghịch biến trên \((\alpha ;\beta ) \Leftrightarrow h(m) \ge {\max _{(\alpha ;\beta )}}g(x)\)

- Nếu bất phương trình \({f^\prime }(x,m) \ge 0 \Leftrightarrow h(m) \le g(x)\) (**) thì f nghịch biến trên \((\alpha ;\beta ) \Leftrightarrow \) \(h(m) \le {\min _{(\alpha ;\beta )}}g(x).\)

Lưu ý: Sử dụng máy tính kiểm tra sự đồng biến, nghịch biến của hàm số.

Cách 1. Áp dụng định nghĩa: Xét hàm số y = f(x) trên khoảng K

- Trên khoảng K, khi x tăng và y tăng suy ra hàm số đồng biến.

- Trên khoảng K, khi x tăng và y giảm suy ra hàm số nghịch biến.

Sử dụng máy tính cầm tay với chức năng TABLE. BẤM MODE 7 , nhập dữ liệu f(X), chọn Start, end và step.

Cách 2. Áp dụng đạo hàm. Xét hàm số y = f(x) trên khoảng K

- Trên khoảng K, nếu \({y^\prime } > 0,\left( {{y^\prime } \ge 0} \right)\) suy ra hàm số đồng biến.

- Trên khoảng K, nếu \({y^\prime } < 0,\left( {{y^\prime } \le 0} \right)\) suy ra hàm số nghịch biến.

Sử dụng máy tính cầm tay với chức năng đạo hàm: Bấm shift . Màn hình: \({\left. {\frac{{\rm{d}}}{{{\rm{d}}x}}(f({\rm{x}}))} \right|_{x = {\rm{x}}}}\) Cần hiểu: \({y^\prime } = {\left. {\frac{d}{{dx}}(f(X))} \right|_{x = X}}\). Nhập hàm số đã cho. Calc giá trị của X thuộc khoảng K theo yêu cầu bài toán tương ứng. Nhận xét và đưa ra kết luận.

B. Bài tập trắc nghiệm

Câu 1: Cho hàm số \(y = 6{x^5} - 15{x^4} + 10{x^3} - 22\). Mệnh đề nào dưới đây đúng ?

A. Hàm số đồng biến trên khoảng \(( - \infty ; + \infty )\).

B. Hàm số đồng biến trên khoảng \(( - \infty ;0)\) và nghịch biến trên khoảng \((0; + \infty )\).

C. Hàm số nghịch biến trên \(\mathbb{R}\).

D. Hàm số nghịch biến trên khoảng (0;1).

Câu 2: Tập các giá trị thực tham số m để hàm số \(y = m{x^3} + 3{x^2} + 12x + 2\) đồng biến trên tập xác định của nó là

A. \(m \in \emptyset \).

B. \(m \in \left[ {\frac{1}{4}; + \infty } \right)\).

C. \(m \in ( - \infty ; - 3]\).

D. \(m \in [0; + \infty )\).

Câu 3: Hàm số \(y = \frac{2}{{{x^2} + 1}}\) nghịch biến trên khoảng nào dưới đây ?

A. \(( - \infty ;0)\).

B. (-1;1).

C. \(( - \infty ; + \infty )\).

D. \((0; + \infty )\).

Câu 4: Cho hàm số f(x), bảng xét dấu của \({f^\prime }(x)\) như sau:

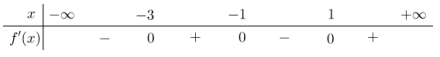
Hàm số \(y = f(5 - 2x)\) đồng biến trên khoảng nào dưới đây ?

A. (1;3).

B. \(( - \infty ; - 3)\).

C. (3;4).

D. (4;5).

Câu 5: Có bao nhiêu giá trị nguyên âm của tham số m để hàm số \(y = \frac{3}{4}{x^4} + (m + 3){x^2} - \frac{1}{{5{x^5}}}\) đồng biến trên khoảng \((0; + \infty )\) ?

A. 5 .

B. 2 .

C. 7 .

D. 4 .

Câu 6: Cho hàm số \(y = \sqrt {2x - {x^2}} \). Mệnh đề nào dưới đây đúng ?

A. Hàm số đồng biến trên khoảng \(( - \infty ;1)\).

B. Hàm số nghịch biến trên khoảng (0;1) và đồng biến trên (1;2).

C. Hàm số đồng biến trên khoảng (0;1) và nghịch biến trên (1;2)..

D. Hàm số nghịch biến trên \((2; + \infty )\).

Câu 7: Cho hàm số \(y = \frac{{{x^2} + (m + 1)x - 1}}{{2 - x}}\) với m là tham số. Tập hợp các giá trị của tham số m để hàm số nghịch biến trên mỗi khoảng xác định của nó là

A. \(m \in ( - \infty ; - 1)\).

B. \(m \in \left( { - \infty ; - \frac{5}{4}} \right)\).

C. \(m \in (1; + \infty )\).

D. \(m \in ( - 1;1)\).

Câu 8: Cho hàm số \(y = {x^3} - 3{x^2}\). Mệnh đề nào dưới đây đúng ?

A. Hàm số nghịch biến trên khoảng \(( - \infty ;0)\).

B. Hàm số đồng biến trên khoảng (0;2).

C. Hàm số nghịch biến trên khoảng (0;2)..

D. Hàm số nghịch biến trên khoảng \((2; + \infty )\).

Câu 9: Tập hợp các giá trị thực của tham số m sao cho hàm số \(y = \frac{{mx + 2}}{{2x + m}}\) đồng biến trên từng khoảng xác định của nó là

A. \(m \in ( - \infty ; - 2) \cup (2; + \infty )\).

B. \(m \in (2; + \infty )\).

C. \( - 2 < m < 2\).

D. \(m \in ( - \infty ; - 2)\).

Câu 10: Cho hàm số f(x) có đạo hàm \({f^\prime }(x) = {(x + 1)^2}{(x - 1)^3}(2 - x)\). Hàm số f(x) đồng biến trên khoảng nào dưới đây?

A. (1;2).

B. \(( - \infty ; - 1)\).

C. (-1;1).

D. \((2; + \infty )\).

Câu 11: Cho hàm số \(y = (1 - m){x^3} + (2m - 1)x - m + 1\) với m là tham số. Tập hợp các giá trị của m để hàm số luôn đồng biến trên tập xác định của nó là

A. \(m \in \left[ {\frac{1}{2};1} \right)\).

B. \(m \in \left( {\frac{1}{2};1} \right)\).

C. \(m \in \left[ {\frac{1}{2};1} \right]\).

D. \(m \in \left( {\frac{1}{2};1} \right]\).

Câu 12: Cho hàm số \(y = \sqrt {{x^2} - x - 20} \). Mệnh đề nào dưới đây đúng ?

A. Hàm số đồng biến trên khoảng (-4;5).

B. Hàm số đồng biến trên khoảng \(( - \infty ; - 4)\) và nghịch biến trên khoảng \((5; + \infty )\).

C. Hàm số nghịch biến trên khoảng (-4;5).

D. Hàm số nghịch biến trên khoảng \(( - \infty ; - 4)\) và đồng biến trên khoảng \((5; + \infty )\).

Câu 13: Cho hàm số \(y = \sqrt {2{x^2} + 1} \). Mệnh đề nào dưới đây đúng ?

A. Hàm số nghịch biến trên khoảng \((0; + \infty )\).

B. Hàm số đồng biến trên khoảng \(( - \infty ;0)\).

C. Hàm số nghịch biến trên khoảng (-1;1).

D. Hàm số đồng biến trên khoảng \((0; + \infty )\).

Câu 14: Cho hàm số \(y =  - {x^3} - m{x^2} + (4m + 9)x + 5\) với m là tham số. Có bao nhiêu giá trị nguyên m để hàm số nghịch biến trên khoảng \(( - \infty ; + \infty )\) ?

A. 5 .

B. 6 .

C. 4 .

D. 7 .

Câu 15: Hàm số \(y = \frac{{2x - 5}}{{x + 3}}\) đồng biến trên khoảng nào dưới đây ?

A. \(( - \infty ;3)\).

B. \(( - 3; + \infty )\).

C. \(( - \infty ; + \infty )\).

D. \(\mathbb{R}\backslash \{  - 3\} \).

Câu 16: Cho hàm số \(y = {x^3} + 3{x^2} - 2mx - 4\) với m là tham số. Tập hợp các giá trị của m để hàm số đồng biến trên khoảng \(( - \infty ;0)\) là

A. \(m \in \left( { - \infty ; - \frac{3}{2}} \right]\).

B. \(m \in \left[ {\frac{3}{2}; + \infty } \right)\).

C. \(m \in ( - 10;1)\).

D. \(m \in (2; + \infty )\).

Câu 17: Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau

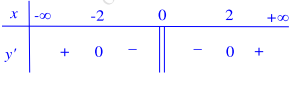
Mệnh đề nào dưới đây đúng ?

A. Hàm số nghịch biến trên khoảng \(( - \infty ; - 2)\).

B. Hàm số nghịch biến trên khoảng (0;2).

C. Hàm số đồng biến trên khoảng (-2;0). \(\quad \)

D. Hàm số đồng biến trên khoảng \(( - \infty ;0)\).

Câu 18: Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + (8 - 2m)x + m + 3\) đồng biến trên tập xác định của nó ?

A. 11 .

B. 3 .

C. 7 .

D. 12 .

Câu 19: Cho hàm số f(x) có bảng biến thiên như sau:

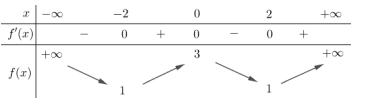
Hàm số đã cho nghịch biến trên khoảng nào dưới đây ?

A. \((2; + \infty )\).

B. (0;2).

C. (-2;0).

D. \((0; + \infty )\).

Câu 20: Cho hàm số \(y = \frac{1}{3}(m - 1){x^3} + m{x^2} + (3m - 2)x\) với m là tham số. Tập hợp các giá trị của m để hàm số luôn đồng biến trên tập xác định của nó là

A. \(m \in [2; + \infty )\).

B. \(m \in ( - \infty ;2]\).

C. \(m \in (2; + \infty )\).

D. \(m \in ( - \infty ;2)\).

Câu 21: Hàm số nào dưới đây đồng biến trên khoảng \(( - \infty ; + \infty )\) ?

A. \(y = {x^3} + x\).

B. \(y =  - {x^3} - 3x\).

C. \(y = \frac{{x + 1}}{{x + 3}}\).

D. \(y = \frac{{x - 1}}{{x - 2}}\).

Câu 22: Cho hàm số \(y = \frac{{ - {x^2} - 2x + 3}}{{x + 1}}\). Mệnh đề nào dưới đây đúng ?

A. Hàm số đồng biến trên các khoảng \(( - \infty ; - 1)\) và \(( - 1; + \infty )\).

B. Hàm số nghịch biến trên các khoảng \(( - \infty ; - 1)\) và \(( - 1; + \infty )\).

C. Hàm số nghịch biến trên các khoảng \(( - \infty ;1)\) và \((1; + \infty )\).

D. Hàm số đồng biến trên các khoảng \(( - \infty ;1)\) và \((1; + \infty )\).

Câu 23: Cho hàm số \(y = \frac{1}{3}(m - 3){x^3} - 2{x^2} + mx + m\) với m là tham số. Tập hợp các giá trị của m để hàm số luôn nghịch biến trên tập xác định của nó là

A. \(m \in ( - 1; + \infty )\).

B. \(m \in [ - 1; + \infty )\).

C. \(m \in ( - \infty ; - 1]\).

D. \(m \in ( - \infty ; - 1)\).

Câu 24: Cho hàm số \(y = \sqrt {4x - {x^2}} \). Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng \(( - \infty ;2)\) và nghịch biến trên khoảng \((2; + \infty )\).

B. Hàm số đồng biến trên khoảng (0;2) và nghịch biến trên khoảng (2,4).

C. Hàm số đồng biến trên khoảng \(( - \infty ;0)\) và nghịch biến trên khoảng \((4; + \infty )\).

D. Hàm số nghịch biến trên khoảng (0;2) và đồng biến trên khoảng (2,4).

Câu 25: Cho hàm số \(y = 2{x^3} + 6{x^2} + 6x - 7\). Mệnh đề nào dưới đây sai ?

A. Hàm số đồng biến trên \(\mathbb{R}\).

B. Hàm số đồng biến trên \(( - \infty ; + \infty )\).

C. Hàm số đồng biến trên khoảng \(( - \infty ;1)\).

D. Hàm số đồng biến trên khoảng \((1; + \infty )\).

Câu 26: Cho hàm số \(y = {x^4} - 2{x^2}\). Mệnh đề nào dưới đây đúng ?

A. Hàm số nghịch biến trên khoảng (-1;1).

B. Hàm số đồng biến trên khoảng \(( - \infty ; - 2)\).

C. Hàm số đồng biến trên khoảng (-1;1).

D. Hàm số nghịch biến trên khoảng \(( - \infty ; - 2)\).

Câu 27: Cho hàm số \(y = \frac{{2x - 1}}{{x + 1}}\). Mệnh đề nào dưới đây đúng ?

A. Hàm số nghịch biến trên các khoảng \(( - \infty ; - 1)\) và \(( - 1; + \infty )\).

B. Hàm số đồng biến trên \(\mathbb{R}\backslash \{  - 1\} \).

C. Hàm số nghịch biến trên \(\mathbb{R}\backslash \{  - 1\} \).

D. Hàm số đồng biến trên các khoảng \(( - \infty ; - 1)\) và \(( - 1; + \infty )\).

Câu 28: Cho hàm số \(y = \frac{4}{5}{x^5} - {x^4} + \frac{{{x^3}}}{3} - 1\). Mệnh đề nào dưới đây đúng ?

A. Hàm số nghịch biến trên \(\mathbb{R}\).

B. Hàm số đồng biến trên khoảng \(( - \infty ; + \infty )\).

C. Hàm số nghịch biến trên khoảng \(( - \infty ;1)\) và đồng biến trên khoảng \((1; + \infty )\).

D. Hàm số đồng biến trên khoảng \(( - \infty ;1)\) và nghịch biến trên khoảng \((1; + \infty )\).

Câu 29: Tập hợp các giá trị thực tham số \(m\) để hàm số \(y = \frac{m}{3}{x^3} - m{x^2} + (2m - 1)x - 2\) nghịch biến trên tập xác định của nó là

A. \(m \in ( - \infty ;0]\).

B. \(m \in [1; + \infty )\).

C. \(m \in ( - \infty ; - 2]\).

D. \(m \in ( - 2;0)\).

Xem thêm