Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết và bài tập tính đơn điệu của hàm số, tài liệu bao gồm 84 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Lý thuyết và bài tập tính đơn điệu của hàm số

CHƯƠNG 1. ỨNG DỤNG ĐẠO HÀM VÀ VẼ ĐỒ THỊ HÀM SỐ

Bài 1. Tính đơn điệu của hàm số

A. Lý thuyết.

1. Định nghĩa:

Giả sử K là một khoảng, một đoạn hoặc một nửa khoảng. Hàm số\[f\]xác định trên K được gọi là :

Hàm số \[y = f(x)\] được gọi là đồng biến (tăng) trên K nếu:

\[\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\].

Khi đó, đồ thị của hàm số đi lên từ trái sang phải.

Hàm số\[y = f(x)\] được gọi là nghịch biến (giảm) trên K nếu:

\[\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\].

Khi đó, đồ thị của hàm số đi xuống từ trái sang phải.

Hình ảnh minh họa sự đồng biến và nghịch biến của hàm số

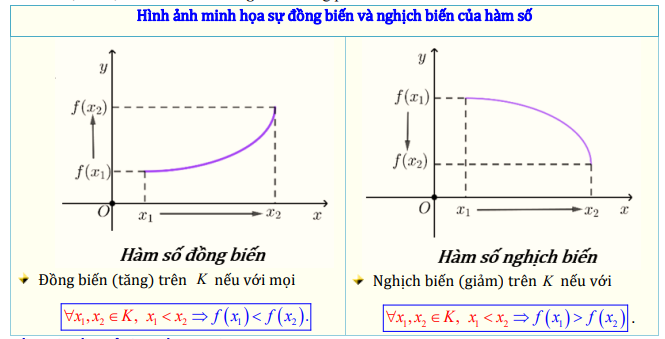
2. Điều kiện cần để hàm số đơn điệu :

Giả sử hàm số\[f\]có đạo hàm trên khoảng I

Nếu hàm số\[f\]đồng biến trên khoảng I thì \[f'(x) \ge 0\]với mọi x Î I

Nếu hàm số\[f\]nghịch biến trên khoảng I thì \[f'(x) \le 0\]với mọi x Î I

3. Điều kiện đủ để hàm số đơn điệu :

3.1. Định lý :

Giả sử I là một khoảng hoặc nửa khoảng hoặc một đoạn, \[f\] là hàm số liên tục trên I và có đạo hàm tại mọi điểm trong của I (tức là điểm thuộc I nhưng không phải đầu mút của I). Khi đó

Nếu\[f'(x) > 0\]với mọi xÎI thì hàm số\[f\] đồng biến trên khoảng I

Nếu\[f'(x) < 0\]với mọi xÎI thì hàm số\[f\]nghịch biến trên khoảng I

Nếu\[f'(x) = 0\]với mọi xÎI thì hàm số\[f\] không đổi trên khoảng I

Chú ý :

Nếu hàm số\[f\] liên tục trên [a;b] và có đạo hàm\[f'(x) > 0\]trên khoảng (a;b) thì hàm số \[f\] đồng biến trên [a;b]

Nếu hàm số\[f\]liên tục trên [a;b] và có đạo hàm\[f'(x) < 0\]trên khoảng (a;b) thì hàm số\[f\] nghịch biến trên [a;b].

3.2. Hệ quả. ta có thể mở rộng định lí trên như sau

Giả sử hàm số\[f\]có đạo hàm trên khoảng I .

Nếu\[f'(x) \ge 0\]với "x Î I ( hoặc\[f'(x) \le 0\]với "x Î I ) và\[f'(x) = 0\] tại một số hữu hạn điểm của I thì hàm số\[f\] đồng biến (hoặc nghịch biến) trên I .

Vận dụng định lí trên vào các hàm số thường gặp trong chương trình.

Nếu hàm số\[f\]là hàm đa thức (không kể hàm số hằng) hoặc \[f(x) = \frac{{P(x)}}{{Q(x)}}\] (trong đó \[P(x)\]là đa thức bậc hai, \[Q(x)\]là đa thức bậc nhất và\[P(x)\]không chia hết cho \[Q(x)\]thì hàm số\[f\]đồng biến (nghịch biến ) trên K Û \[\forall x \in K,f'(x) \ge 0(f'(x) \le 0).\]

Nếu hàm số\[f\]là hàm nhất biến \[f(x) = \frac{{ax + b}}{{cx + d}}\] với a, b, c, d là các số thực và ad - bc ¹ 0 thì hàm số f đồng biến (nghịch biến ) trên K Û \[\forall x \in K,f'(x) > 0(f'(x) < 0).\]

B. Phương pháp giải toán.

Dạng 1. Xét tính đơn điệu của hàm số

1. Phương pháp .

Bước 1. Tìm tập xác định của hàm số\[f\].

Bước 2. Tính đạo hàm\[f'(x)\]và tìm các điểm x₀ sao cho \[f'({x_0}) = 0\]hoặc \[f'({x_0})\] không xác định .

Bước 3. Lập bảng xét dấu\[f'(x)\], dựa vào định lí 1, nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số .

2. Bài tập minh họa .

Bài tập 1. Tìm các khoảng đồng biến, nghịch biến (hoặc xét chiều biến thiên) của hàm số:

1). \[y = \frac{4}{3}{x^3} - 2{x^2} + x - 3\]

2). \[y = {x^3} - 6{x^2} + 9x - 3\]

Bài tập 2. Tìm các khoảng đồng biến, nghịch biến (hoặc xét chiều biến thiên) của hàm số:

1). \[y =  - \frac{1}{4}{x^4} - \frac{3}{2}{x^2} + 1\]

2). \[y =  - \frac{1}{4}{x^4} + {x^3} - 4x + 1\]

Bài tập 3. Tìm các khoảng đồng biến, nghịch biến (hoặc xét chiều biến thiên) của hàm số:

1). \[y = \frac{{x - 2}}{{x - 1}}\]

2). \[y = \frac{{2x - 1}}{{x - 1}}\]

Bài tập 4. Tìm các khoảng đồng biến, nghịch biến (hoặc xét chiều biến thiên) của hàm số:

1). \[y = \frac{{{x^2} + 4x + 4}}{{x + 1}}\]

2). \[y = \frac{{4{x^2} + 5x + 5}}{{x + 1}}\]

Bài tập 5. Tìm các khoảng đồng biến, nghịch biến (hoặc xét chiều biến thiên) của hàm số:

1). \[y = \left| {{x^2} - 2x - 3} \right|\]

2). \[y = \left| {{x^2} - 4x + 3} \right| + 2x + 3\]

Nhận xét:

Bài toán xét tính đơn điệu của hàm số được chuyển về bài toán xét dấu của một biểu thức (y ').

Khi tính đạo hàm của hàm số có dạng \[y = \left| {f(x)} \right|\] ta chuyển trị tuyệt đối vào trong căn thức \[y = \sqrt {{f^2}(x)} \], khi đó tại những điểm mà \[f(x) = 0\] thì hàm số không có đạo hàm

Bài tập 6. Tìm các khoảng đồng biến , nghịch biến (hoặc xét chiều biến thiên) của hàm số:

1). \[y = \frac{{4x + 5}}{{4{x^2} - 4}}\]

2). \[y = \frac{{12x + 1}}{{12{x^2} + 2}}\]

3). \[y = \frac{{3{x^2} - x + 1}}{{{x^2} - x + 1}}\]

Bài tập 7. Tìm các khoảng đồng biến, nghịch biến (hoặc xét chiều biến thiên) của hàm số:

1). \[y = x + \sqrt {2x - {x^2}} \]

2). \[y = (2 + 1)\sqrt {9 - {x^2}} \]

3). \[y = \sqrt {{x^2} - x - 20} \]