Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 138 Bài toán chọn lọc tính đơn điệu của hàm hợp, tài liệu bao gồm 102 trang, 138 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

138 Bài toán chọn lọc tính đơn điệu của hàm hợp - có đáp án chi tiết

Xét tính đơn điệu của hàm số \[y = f(x) + g(x)\].

Xét tính đơn điệu của hàm số \[f(u)\]với \[u\]là một hàm số đối với biến x

Phương pháp:

Tính đạo hàm \[y'\] (nếu có)

Giải các bất phương trình \[y' > 0;y' < 0\]hoặc lập bảng xét dấu của \[y'\].

Đưa ra kết luận

Chú ý: Với hàm số hợp \[y = f(u)\] có\[y' = u'.f'(u)\].

Với hàm hợp \[y = {\left( {f(u)} \right)^n}\]có\[y' = n{\left( {f(u)} \right)^{n - 1}}.\left[ {u'f'(u)} \right]\].

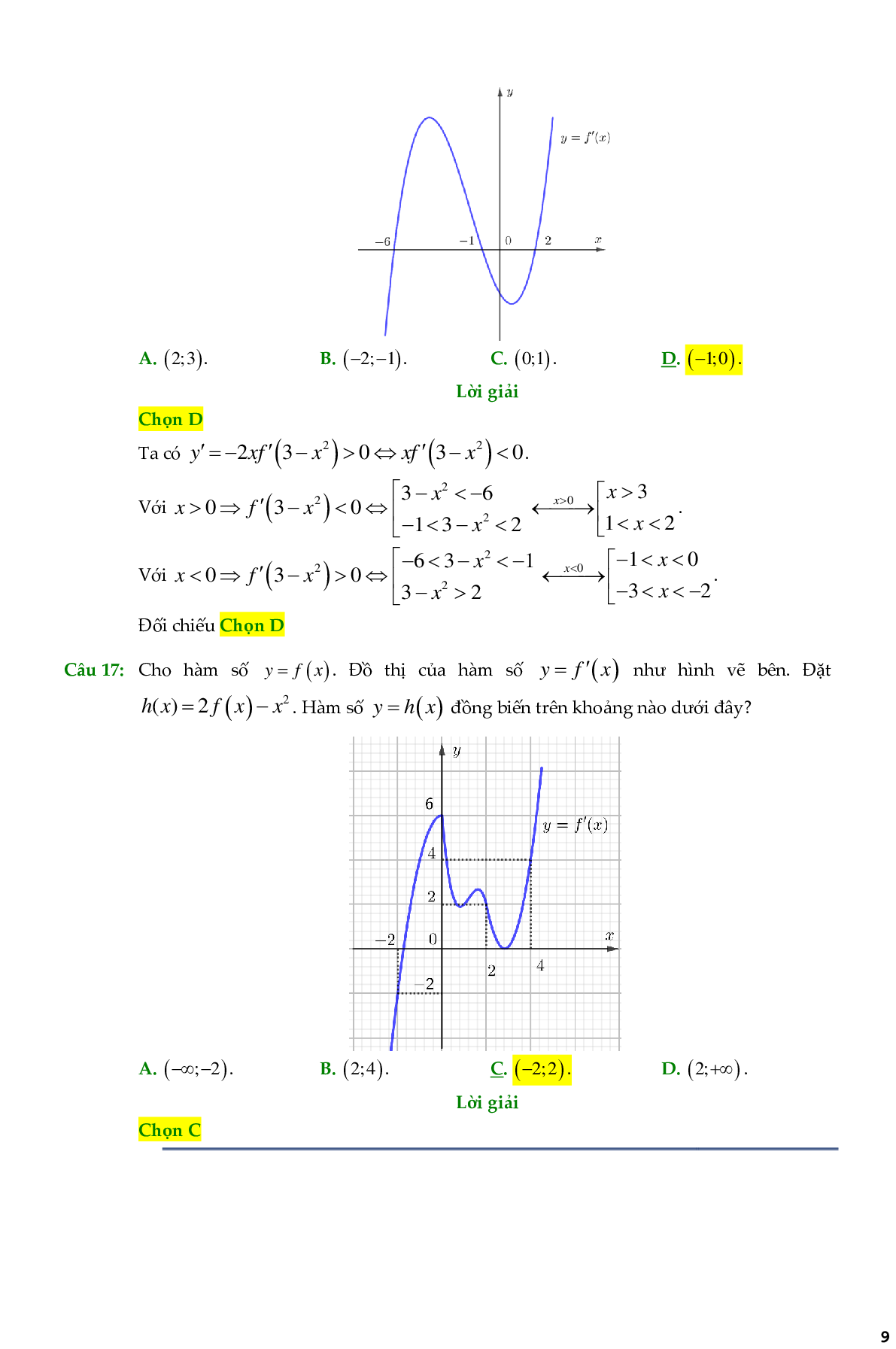
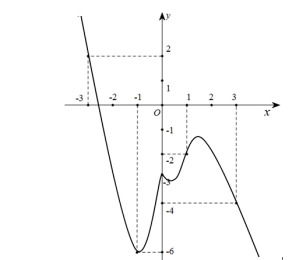
Câu 1: Cho hàm số \[y = f(x)\]. Đồ thị hàm số \[y = f'(x)\] như hình vẽ bên. Hàm số \[g(x) = 2f(x) + {(x + 1)^2}\] đồng biến trên khoảng nào?

A. (-3;1)

B. (1;3)

C. (-∞;3)

D. (3;+∞)

Lời giải

Ta có \[y' = 2f'(x) + 2x + 2 > 0 \Leftrightarrow f'(x) >  - x - 1\]

Kẻ đường thẳng y = – x – 1 qua các điểm  (-3;2), (-2;1), (3;-4)

Ta có \[f'(x) >  - x - 1 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x <  - 3}\\{1 < x < 3}\end{array}} \right.\].

Xét khoảng mà đồ thị hàm số \[y = f'(x)\] nằm bên trên đường thẳng y = – x – 1 suy ra hàm số \[y = g(x)\]đồng biến trên khoảng (1;3).

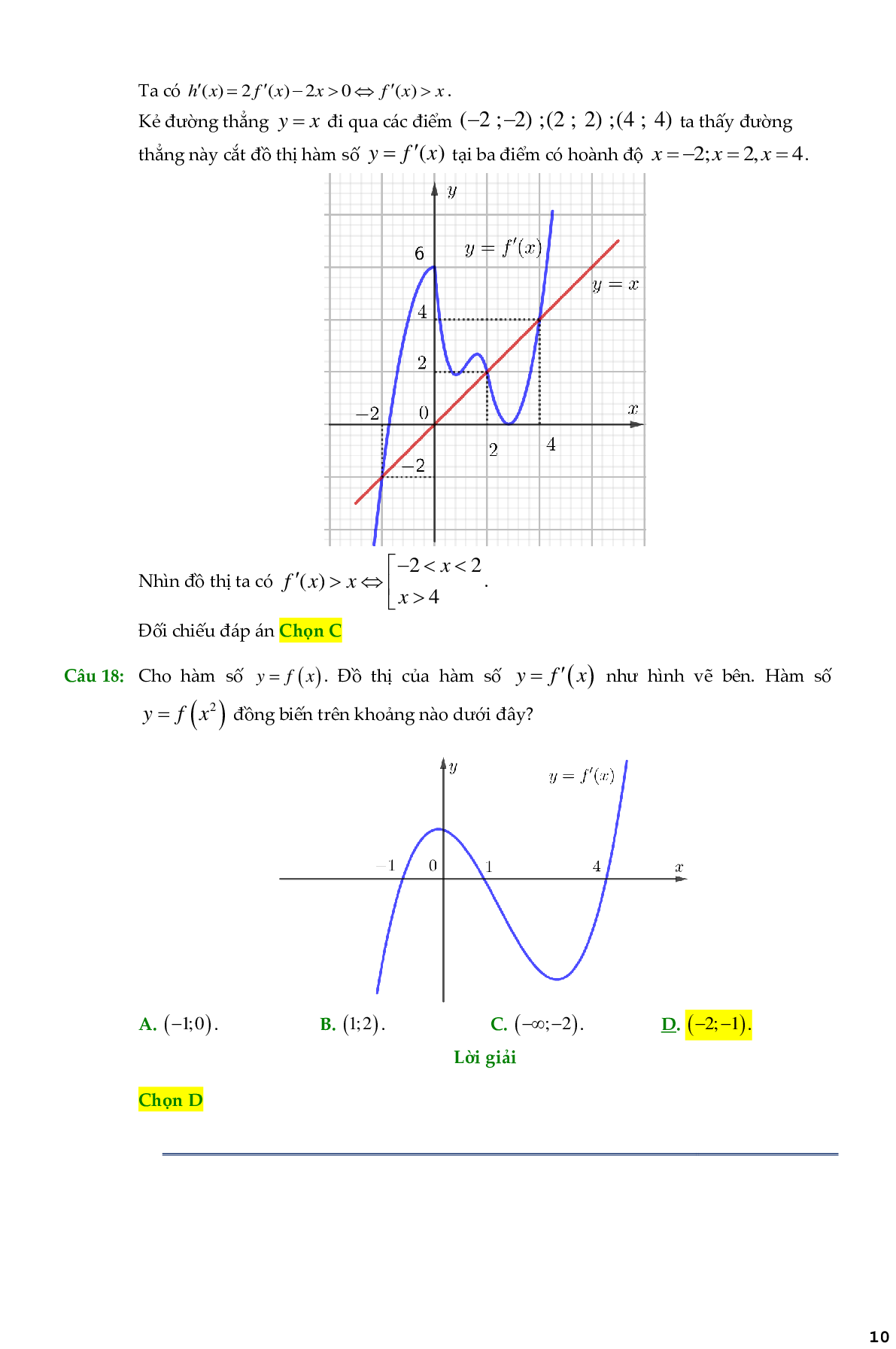
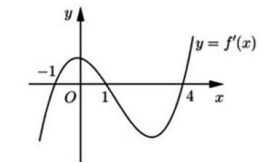
Câu 2. Cho hàm số \[y = f(x)\]. Hàm số\[y = f'(x)\] có đồ thị như hình vẽ bên. Hàm số \[y = f(2 - x)\] đồng biến trên khoảng

A. (1;3)

B. (2;+∞)

C. (-2;1)

D. (-∞;-2)

Lời giải

Chọn C

Ta có

\[\begin{array}{l}y =  - f'(2 - x) > 0 \Leftrightarrow f'(2 - x) < 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2 - x <  - 1}\\{1 < 2 - x < 4}\end{array} \Leftrightarrow } \right.\left[ {\begin{array}{*{20}{c}}{x > 3}\\{ - 2 < x < 1}\end{array}} \right.\end{array}\]

Do đó, hàm số \[y = f(2 - x)\] đồng biến trên khoảng (-2;1).

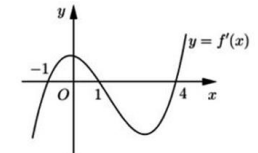
Câu 3. Cho hàm số \[y = f(x)\]. Hàm số\[y = f'(x)\] có đồ thị như hình vẽ bên. Hàm số \[y = f({x^2} - 2)\] đồng biến trên khoảng

A. (0; \[\sqrt 6 \])

B. (0;1)

C. (-\[\sqrt 3 \];0)

D.(1; \[\sqrt 3 \])

Lời giải

Chọn D

Ta có \[y' = 2x.f'({x^2} - 2) > 0\]

Nếu \[x > 0\] thì \[f'({x^2} - 2) > 0\]

\[ \Leftrightarrow f'(2 - x) > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 1 < {x^2} - 2 < 1}\\{{x^2} - 2 > 4}\end{array}} \right.\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{1 < {x^2} < 3}\\{{x^2} > 6}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{1 < x < \sqrt 3 }\\{x > \sqrt 6 }\end{array}} \right.} \right.\]

Nếu \[x < 0\] thì \[f'({x^2} - 2) < 0\]

\[ \Leftrightarrow f'(2 - x) < 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{1 < {x^2} - 2 < 4}\\{{x^2} - 2 <  - 1}\end{array}} \right.\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3 < {x^2} < 6}\\{{x^2} < 1}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 1 < x < 0}\\{ - \sqrt 6  < x <  - \sqrt 3 }\end{array}} \right.} \right.\]

Do đó, trong các đáp án đã cho thì hàm số\[y = f({x^2} - 2)\]đồng biến trên khoảng (1;\[\sqrt 3 \])

Câu 4. Cho hàm số \[y = f(x)\]có đạo hàm \[y = {x^2}(x - 1)({x^2} - 4)\]. Hàm số \[y = f(2 - x)\] có  đồng biến trên khoảng

A. (-∞;0)

B. (0;1)

C. (2;+∞)

D. (1;4)

Lời giải

Chọn B

Ta có

\[\begin{array}{l}y' = f'(2 - x) = 2x.f'(2 - x)\\ = 2x{(2 - x)^2}(2 - x - 1)\left( {{{(2 - x)}^2} - 4} \right)\end{array}\]

Do đó \[y' =  - {(2 - x)^2}(1 - x)\left( {{x^2} - 4x} \right)\].

Suy ra

\[\begin{array}{l}y' > 0 \Leftrightarrow (x - 1){(x - 2)^2}({x^2} - 4x) > 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{0 < x < 1}\\{x > 4}\end{array}} \right.\end{array}\]

Vậy, từ các đáp án đã cho ta có hàm số đồng biến trên khoảng (0;1).

Câu 5. Cho hàm số \[y = f(x)\] có bảng biến thiên như sau:

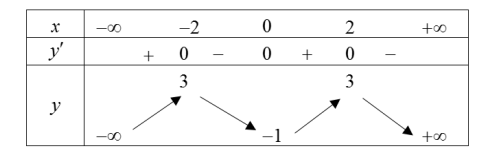
Hàm số \[y = {x^2} - 2\]nghịch biến trên khoảng nào dưới đây

A. (-2;0)

B. (2;+∞)

C. (0;2)

D. (-∞;0)

Lời giải

Chọn B

Ta có \[y' = f'(2 - x) = 2x.f'({x^2} - 2) = 2x.f'({x^2} - 2) < 0\]

Nếu \[x > 0\] thì \[y' < 0 \Leftrightarrow f'({x^2} - 2) < 0\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 2 < {x^2} - 2 < 0}\\{{x^2} - 2 > 2}\end{array} \Leftrightarrow } \right.\left[ {\begin{array}{*{20}{c}}{x > 2}\\{0 < x < \sqrt 2 }\end{array}} \right.\]

Nếu \[x < 0\] thì \[y' > 0 \Leftrightarrow f'({x^2} - 2) > 0\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x^2} - 2 <  - 2}\\{0 < {x^2} - 2 < 2}\end{array} \Leftrightarrow } \right. - 2 < x <  - \sqrt 2 \]

Do đó, đáp án đúng trong các đáp án đã cho hàm số khoảng (2;+∞).

Câu 6. Cho hàm số \[y = f(x)\]có đạo hàm \[f'(x) = x{(x - 1)^2}(x - 2)\]. Hàm số \[y = f\left( {\frac{{5x}}{{{x^2} + 4}}} \right)\] đồng biến trên khoảng nào dưới đây?

A. (-∞;-2)

B.(0;2)

C. (2;4)

D. (-2;1)

Lời giải

Chọn C

Ta có:

$$\begin{gathered} y\text{'}={\left(\frac{5x}{x^2+4}\right)}^{\text{'}}f\text{'}\left(\frac{5x}{x^2+4}\right) \\ =\frac{5(4-x^2)}{{\left(x^2+4\right)}^2}.\frac{5x}{x^2+4}{\left(\frac{5x}{x^2+4}-1\right)}^2\left(\frac{5x}{x^2+4}-2\right) \end{gathered}$$

Do đó:

\[\begin{array}{l}y' > 0 \Leftrightarrow (4 - {x^2}){(5x - {x^2} - 4)^2}(5x - 2{x^2} - 8) > 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x > 4}\\\begin{array}{l}2 < x < 4\\ - 2 < x < 0\end{array}\end{array}} \right.\end{array}\]

Đối chiếu các phương án ta chọn C.

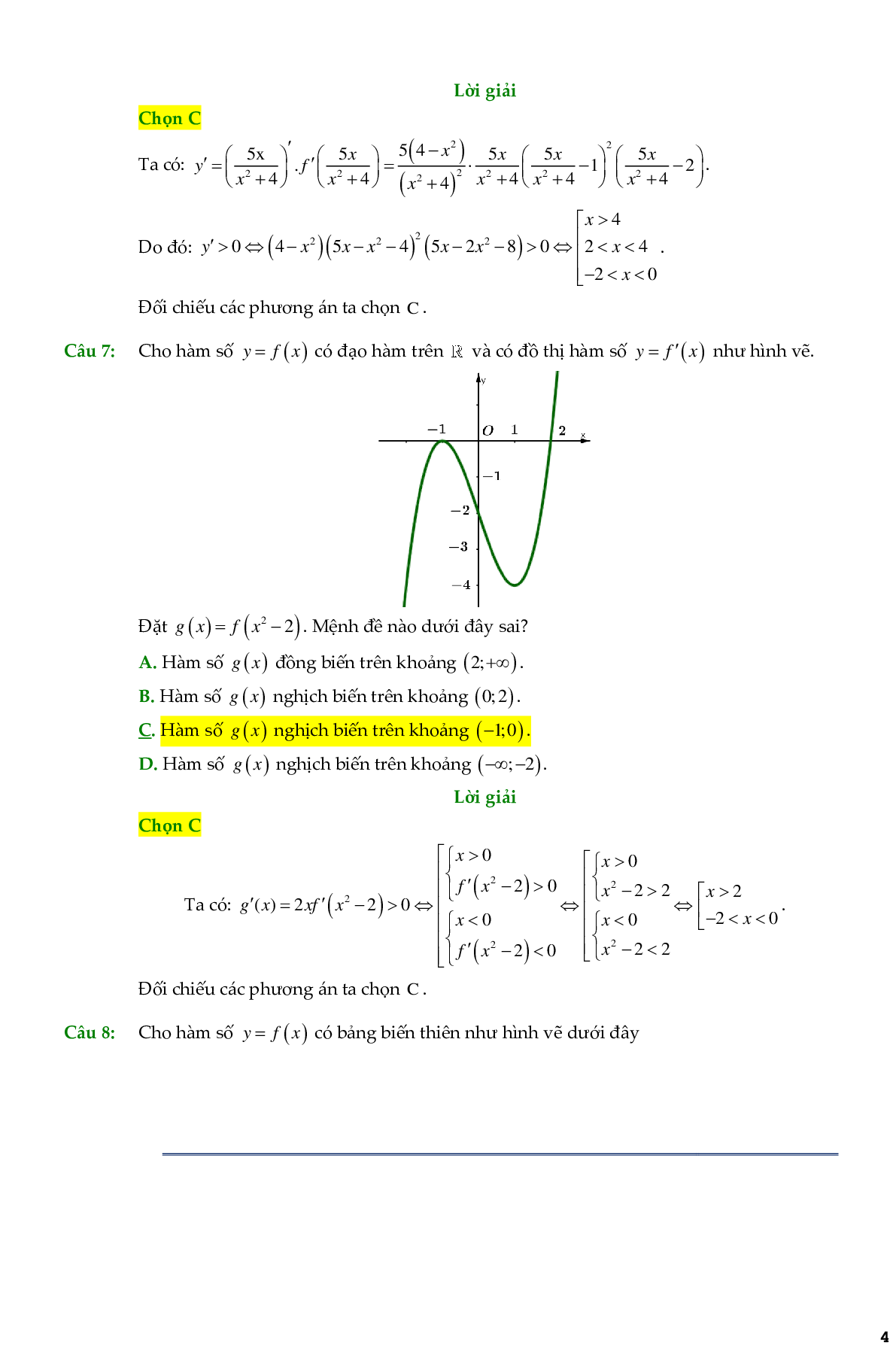
Câu 7. Cho hàm số \[y = f(x)\] có đạo hàm trên R và có đồ thị hàm số \[y = f'(x)\] như hình vẽ

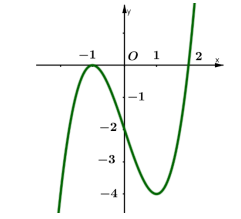
Đặt \[g(x) = f({x^2} - 2)\]. Mệnh đề nào dưới đây sai?

A. Hàm số \[g(x)\] đồng biến trên khoảng (2;+∞)

B. Hàm số \[g(x)\] nghịch biến trên khoảng (0;2)

A. Hàm số \[g(x)\] đồng biến trên khoảng (-1;0)

A. Hàm số \[g(x)\] đồng biến trên khoảng (-∞;-2)

Lời giải

Chọn C

Ta có:

\[\begin{array}{l}g'(x) = 2xf'({x^2} - 2) > 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{x > 0}\\{f'({x^2} - 2) > 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{x < 0}\\{f'({x^2} - 2) < 0}\end{array}} \right.}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{x > 0}\\{{x^2} - 2 > 2}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{x < 0}\\{{x^2} - 2 < 2}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x > 2}\\{ - 2 < x < 0}\end{array}} \right.\end{array}\]

Đối chiếu các phương án ta chọn C

Câu 8. Cho hàm số \[y = f(x)\]có bảng biến thiên như hình vẽ dưới đây

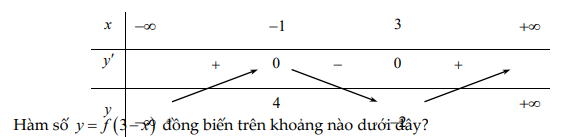
A. (-∞;0)

B. (4;6)

C. (-1;5)

D. (0;4)

Lời giải

Chọn D

Ta có

\[\begin{array}{l}y' =  - f'(3 - x) > 0 \Leftrightarrow f'(3 - x) < 0\\ \Leftrightarrow  - 1 < 3 - x < 3 \Leftrightarrow 0 < x < 4\end{array}\]

Vậy hàm số \[y = f(3 - x)\]đồng biến trên khoảng (0;4).

Câu 9: Cho hàm số \[y = f(x)\]có đạo hàm \[f'(x) = {x^2}(x - 1)(x - 4)g(x)\], trong đó \[g(x) > 0,\forall x\]. Hàm số \[y = f({x^2})\]đồng biến trên khoảng nào dưới đây?

A. (-∞;-2)

B. (-1;1)

C. (-2;-1)

D. (1;2)

Lời giải

Chọn C

Ta có \[y' = 2xf'({x^2}) = 2x{\left( {{x^2}} \right)^2}({x^2} - 1)({x^2} - 4)g({x^2})\]

\[ = 2{x^5}(x + 1)(x + 2)(x - 1)(x - 2)g({x^2})\]

Ta có \[y' > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x > 2}\\{ - 2 < x <  - 1}\\{0 < x < 1}\end{array}} \right.\].

Vậy hàm số \[y = f({x^2})\]đồng biến trên mỗi khoảng (-2;-1), (0;1), (2;+∞).

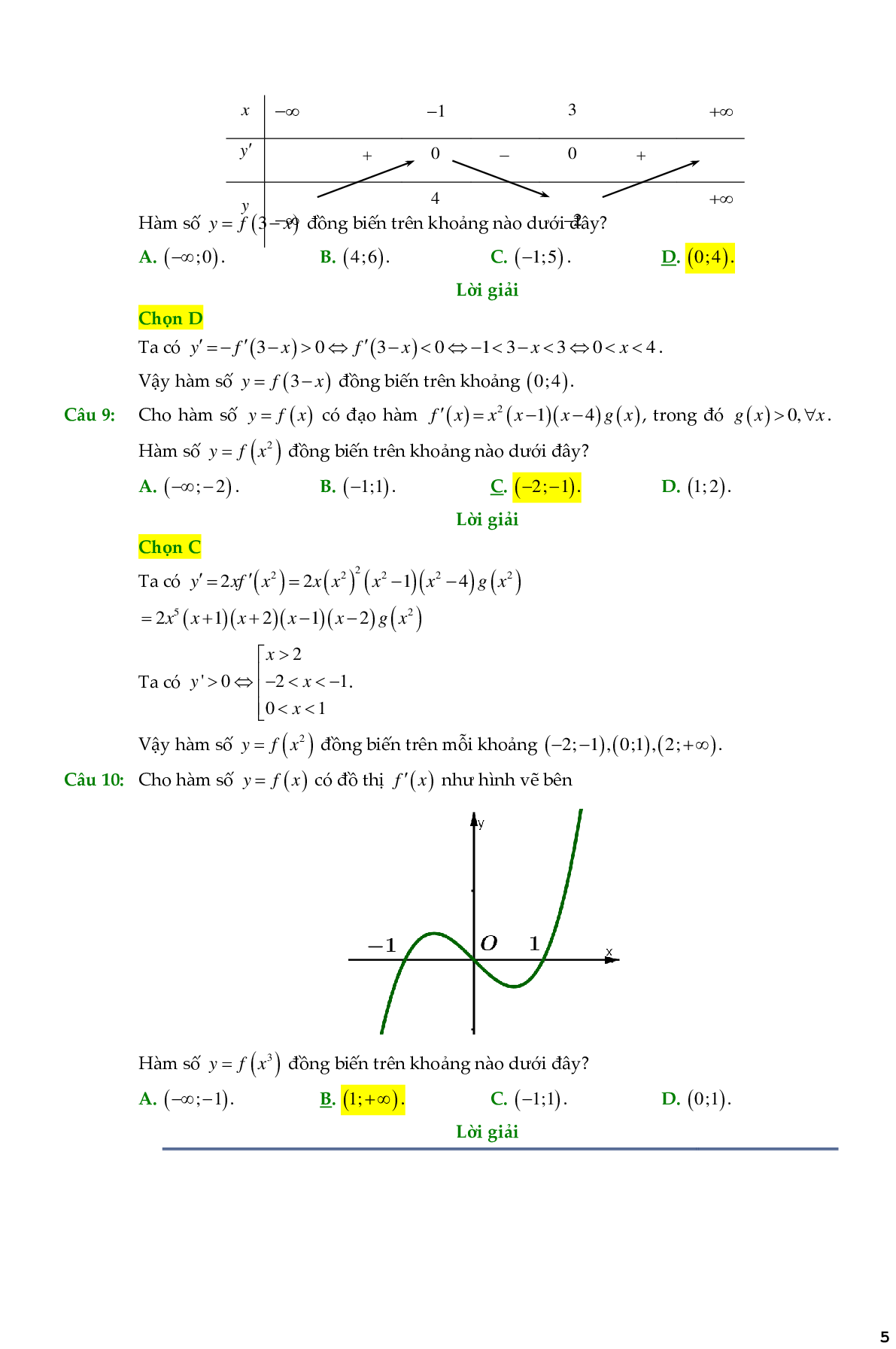
Câu 10. Cho hàm số \[y = f(x)\] có đồ thị \[f'(x)\] như hình vẽ bên

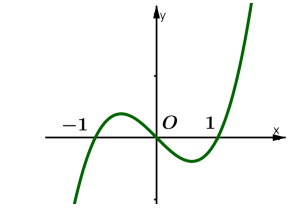
Hàm số \[y = f({x^3})\] đồng biến trên khoảng nào dưới đây?

A. (-∞;-1)

B. (1;+∞)

C. (-1;1)

D. (0;1)