Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bài tập xác định tâm, bán kính, diện tích và thể tích của mặt cầu, tài liệu bao gồm 12 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Bài tập xác định tâm, bán kính, diện tích và thể tích của mặt cầu

Xác định tâm, bán kính, diện tích và thể tích của mặt cầu

I. Kiến thức cần nhớ:

Phương trình mặt cầu dạng chính tắc:

Cho mặt cầu có tâm \[I(a;b;c)\], bán kính R . Khi đó phương trình chính tắc của mặt cầu là \[(S):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\]

Phương trình mặt cầu dạng khai triển là

\[(S):{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\]

Khi đó mặt cầu có có tâm \[I(a;b;c)\], bán kính \[R = \sqrt {{a^2} + {b^2} + {c^2} - d} \]

(\[{a^2} + {b^2} + {c^2} - d > 0\])

Bài tập mẫu

Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu\[(S):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 9\]. Tìm tọa độ tâm I và tính bán kính R của (S).

A. I (-1;2;1) và R = 3

B. I (1; -2; -1) và R = 3

C. I (-1;2;1) và R = 9

D. I (1; -2; -1) và R = 9

Phân tích hướng dẫn giải

1. Dạng toán: Đây là dạng toán sử dụng tính chất để xác định tâm và bán kính của mặt cầu.

2. Hướng giải:

B1: Dựa trên phương trình mặt cầu dạng chính tắc tìm tâm và bán kính của mặt cầu. B2: Mặt cầu \[(S):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\]có tâm \[I(a;b;c)\], bán kính R .

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn B

Mặt cầu \[(S):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 9\] có tâm I (-1;2;1) và bán kính R = 3.

Bài tập tương tự:

Câu 14.1: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình \[{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {z^2} = 9\]. Tìm tọa độ tâm I và bán kính R của mặt cầu đó

A. I (-1;3;0) ; R = 3.

B. I (1; -3;0) ; R = 9 .

C. I (1; -3;0) ; R = 3.

D. I (-1;3;0) ; R = 9 .

Lời giải

Chọn C

Mặt cầu đã cho có tâm I (1; -3;0) và bán kính R = 3.

Câu 14.2: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \[(S):{x^2} + {y^2} + {z^2} - 6x + 4y - 8z + 4 = 0\]. Tìm tọa độ tâm I và tính bán kính R của mặt cầu (S).

A. I (3; -2;4), R = 25 .

B. I (-3;3; -4), R = 5.

C. I (3; -2;4), R = 5.

D. I (-3;2; -4), R = 25 .

Lời giải

Chọn C

Mặt cầu (S) có tâm là I (3; -2; 4) .

Bán kính của mặt cầu (S) là \[R = \sqrt {{{( - 3)}^2} + {{( - 2)}^2} + {{(4)}^2} - 4}  = 5\].

Câu 14.3: Trong không gian Oxyz, diện tích của mặt cầu \[(S):3{x^2} + 3{y^2} + 3{z^2} + 6x + 12y + 18z - 3 = 0\] bằng

A. 20p .

B. 40p .

C. 60p .

D. 100p .

Lời giải

Chọn C

Ta có \[3{x^2} + 3{y^2} + 3{z^2} + 6x + 12y + 18z - 3 = 0\]

\[ \Leftrightarrow {x^2} + {y^2} + {z^2} + 2x + 4y - 6z - 1 = 0\]

Mặt cầu (S ) có tâm là I (-1;-2;3).

Bán kính của mặt cầu (S) là \[R = \sqrt {{{( - 1)}^2} + {{( - 2)}^2} + {{(3)}^2} + 1}  = \sqrt {15} \].

Diện tích mặt cầu V =4pR² = 60p .

Câu 14.4: Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình \[{x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 5 = 0\]. Tính diện tích mặt cầu (S).

A. 42p .

B. 36p .

C. 9p .

D. 12p .

Lời giải

Chọn B

Mặt cầu (S) có tâm I (1;2;3) và bán kính \[R = \sqrt {{1^2} + {2^2} + {3^2} - 5}  = 3\].

Diện tích mặt cầu (S) là: S = 4pR² = 4p3² = 36p .

Câu 14.5: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \[(S):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {z^2} = 9\]. Mặt cầu (S) có thể tích bằng

A. V =16p .

B. V = 36p .

C. V =14p .

D. V = \[\frac{4}{{36}}\]p .

Lời giải

Chọn B

Mặt cầu \[(S):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {z^2} = 9\]có tâm là (1;-2;0) , bán kính R = 3.

Thể tích mặt cầu \[V = \frac{4}{3}\pi {R^3} = 36\pi \]

Bài tập tương tự và phát triển:

Câu 14.6: Trong không gian Oxyz, cho điểm I (1;0; 2) và đường thẳng \[d:\frac{{x - 1}}{2} = \frac{y}{{ - 1}} = \frac{z}{1}\]. Gọi (S ) là mặt cầu có tâm I, tiếp xúc với đường thẳng d. Bán kính của (S) bằng

A. \[\frac{{2\sqrt 5 }}{3}\].

B. \[\frac{5}{3}\].

C. \[\frac{{4\sqrt 2 }}{3}\].

D. \[\frac{{\sqrt {30} }}{3}\].

Phân tích hướng dẫn giải

1. Dạng toán: Đây là dạng toán sử dụng tính chất để xác định tâm và bán kính của mặt cầu.

2. Hướng giải:

B1: Dựa vào vị trí tương đối của đường thẳng và mặt cầu ta tìm được bán kính của mặt cầu \[R = d\left( {I;d} \right)\].

B2: Dựa vào công thức tính khoảng cách từ một điểm dến đường thẳng ta tìm bán kính \[R = \frac{{\left| {\left[ {\overrightarrow {MI} ;\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = \frac{{\sqrt {30} }}{3}\].

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn D

d qua M (1;0;0) và có một vectơ chỉ phương \[\overrightarrow u (2; - 1;1)\]

Bán kính mặt cầu bằng khoảng cách từ I đến d nên ta có: \[R = \frac{{\left| {\left[ {\overrightarrow {MI} ;\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = \frac{{\sqrt {30} }}{3}\]

Câu 14.7: Trong không gian với hệ tọa độ Oxyz, cho điểm I (1; -2;3). Bán kính mặt cầu tâm I, tiếp xúc với trục Oy là

A. \[\sqrt {10} \].

B. \[\sqrt 5 \].

C. 5 .

D. 10.

Lời giải

Chọn A

Gọi M là hình chiếu vuông góc của tâm I (1;-2;3) lên trục Oy, suy ra M (0; -2;0).

Vì mặt cầu tiếp xúc với trục Oy nên có bán kính \[R = IM = \sqrt {10} \].

Câu 14.8: Trong không gian Oxyz, mặt cầu có tâm I (1;0;-2) và tiếp xúc với mặt phẳng (a): x + 22y – 2z + 4 = 0 có đường kính là

A. 3.

B. 5.

C. 6 .

D. 2 .

Phân tích hướng dẫn giải

1. Dạng toán: Đây là dạng toán sử dụng tính chất để xác định tâm và bán kính của mặt cầu.

2. Hướng giải:

B1: Dựa vào vị trí tương đối của mặt phẳng và mặt cầu ta tìm được bán kính của mặt cầu \[R = d\left( {I;(\alpha )} \right)\].

B2: Dựa vào công thức tính khoảng cách từ một điểm đến mặt phẳng ta tìm bán kính \[R = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\].

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn C

Ta có \[R = d\left( {I;(\alpha )} \right) = \frac{{\left| {1 + 4 + 4} \right|}}{3} = 3\].

Đường kính là 2R = 6.

Câu 14.9: Trong không gian Oxyz, mặt cầu có tâm A(2;1;1) và tiếp xúc với mặt phẳng (Oxy) có bán kính là

A. 5.

B. 3.

C. 2 .

D. 1.

Lời giải

Chọn D

Gọi M là hình chiếu vuông góc của tâm A(2;1;1) lên mặt phẳng (Oxy), suy ra M (2;1;0). Vì mặt cầu tiếp xúc với mặt phẳng (Oxy) nên có bán kính R = AM =1.

Câu 14.10: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \[(P):x - 2y + 2z - 2 = 0\]và điểm I (-1;2;-1). Bán kính mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 5 là

A. \[\sqrt {34} \].

B. \[\sqrt 5 \].

C. 5 .

D. 10.

Phân tích hướng dẫn giải

1. Dạng toán: Đây là dạng toán sử dụng tính chất để xác định tâm và bán kính của mặt cầu.

2. Hướng giải:

B1: Dựa vào vị trí tương đối của mặt phẳng và mặt cầu ta tìm được bán kính của mặt cầu \[R = d\left( {I;(\alpha )} \right)\].

B2: Dựa vào công thức \[R = \sqrt {{d^2} + {r^2}} \]ta tìm bán kính của mặt cầu, với d là khoảng cách từ tâm của mặt cầu đến mặt phẳng cắt, r là bán kính của đường tròn giao tuyến của mặt phẳng và mặt cầu.

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn A

Ta có \[d = d\left( {I;(\alpha )} \right) = \frac{{\left| { - 1 - 4 - 2 - 2} \right|}}{3} = 3\]

\[{R^2} = {d^2} + {r^2} = 34\]

Bán kính \[R = \sqrt {34} \].

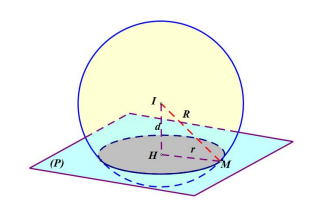
Câu 14.11: Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu (S) có tâm I(-2;3;4) cắt mặt phẳng tọa độ (Oxz) theo một hình tròn giao tuyến có diện tích bằng 16p có thể tích bằng

A. 80p .

B. \[\frac{{500}}{3}\]p .

C. 100p .

D. 25p .

Lời giải

Chọn B

Gọi R , r lần lượt là bán kính mặt cầu và bán kính đường tròn giao tuyến.

Hình tròn giao tuyến có diện tích bằng 16p Û = pr² = 16p Û r = 4.

Khoảng cách từ I(-2;3;4) đến (Oxz) là h = |y_I| = 3.

Suy ra \[R = \sqrt {{h^2} + {r^2}}  = \sqrt {16 + 9}  = 5\].

Thể tích của mặt cầu (S) là \[V = \frac{4}{3}\pi {R^3} = \frac{{500}}{3}\pi \].

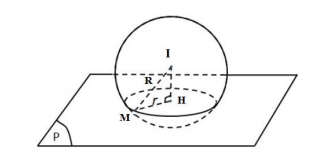
Câu 14.12: Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu (S) có tâm I (-1;2;3) cắt mặt phẳng (b ): 2x – y + 2z – 8 = 0 theo một hình tròn giao tuyến có chu vi bằng bằng 8p có diện tích bằng

A. 80p .

B. 50p .

C. 100p .

D. 25p .

Lời giải

Chọn A

Đường tròn giao tuyến có chu vi bằng 8p nên bán kính của nó là r = 4 .

Khoảng cách từ tâm mặt cầu tới mặt phẳng giao tuyến là \[d = d\left( {I;(\beta )} \right) = \frac{{\left| { - 2 - 2 + 6 - 8} \right|}}{{\sqrt {{2^2} + {1^2} + {2^2}} }} = 2\]

Theo công thức \[{R^2} = {r^2} + {d^2} = 20\].

Diện tích của mặt cầu (S) là S = 4pR² = 80p .

Câu 14.13: Trong không gian Oxyz cho các mặt phẳng \[(P):x - y + 2z + 1 = 0\], \[(Q):2x + y + z - 1 = 0\]. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu.

A. \[r = \sqrt 3 \]

B. \[r = \sqrt {\frac{3}{2}} \]

C. \[r = \sqrt 2 \]

D. \[r = \frac{{3\sqrt 2 }}{2}\]