Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết và bài tập về khối đa diện mặt nón - mặt trụ - mặt cầu, tài liệu bao gồm 61 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Lý thuyết và bài tập về khối đa diện mặt nón - mặt trụ - mặt cầu

Chương 1. Khối đa diện

Bài 1. Khái niệm về khối đa diện

A. Kiến thức giáo khoa cần nắm

I. Khối lăng trụ và khối chóp

Quan sát khối rubic trong hình 1.1, ta thấy các mặt ngoài của nó tạo thành một hình lập phương. Khi đó ta nói khối rubic có hình dáng là một khối lập phương. Như vậy có thể xem khối lập phương là phần không gian được giới hạn bởi một hình lập phương, kể cả hình lập phương ấy.

Tương tự, khối lăng trụ là phần không gian giới hạn bởi một hình lăng trụ, kể cả hình lăng trụ ấy, khối chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp ấy, khối chóp cụt là phân không gian giới hạn bởi 1 hình chóp cụt kể cả hình chóp cụt ấy.

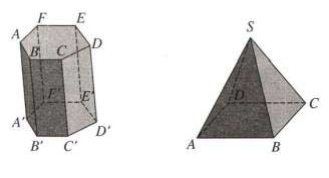
Tên của khối lăng trụ hay khối chóp được đặt theo tên của hình lăng trụ hay hình chóp giới hạn nó. Chẳng hạn ứng với hình lăng trụ lục giác \({\rm{ABCDEF}}{{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }{{\rm{E}}^\prime }{{\rm{F}}^\prime }\) ta có khối lăng trụ lục giác \(ABCDEF.{A^\prime }{B^\prime }{C^\prime }{D^\prime }{E^\prime }{F^\prime }\), ứng với hình chóp tứ giác S.ABCD đều ta có khối chóp tứ giác đều S.ABCD .

II. Khái niệm về hình đa diện và khối đa diện

1. Khái niệm về hình đa diện

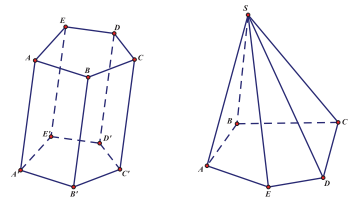
Quan sát hình lăng trụ, hình chóp ở trên ta thấy chúng đều là những hình không gian được tạo bởi một số hữu hạn đa giác. Các đa giác ấy có tính chất

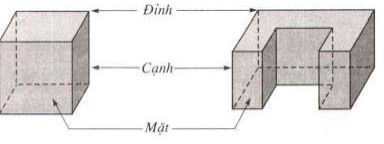
a) Hai đa giác phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.

b) Mỗi canh của đa giác nào cũng là cạnh chung của đúng hai đa giác. Mỗi đa giác như thế được gọi là một mặt của hình đa diện (H). Các đỉnh, cạnh của các đa giác ấy theo thứ tự gọi là các đỉnh, cạnh của hình đa diện (H).

Người ta gọi các hình đó là hình đa diện.

Nói một cách tổng quát: Hình đa diện (gọi tắt là đa diện) (H) là hình được tạo bởi một số hũu hạn các đa giác thỏa mãn hai tính chất trên. Mỗi đa giác như thế được gọi là các mặt của đa diện. Các đỉnh các cạnh của đa giác ấy theo thứ tự được gọi là các đỉnh, cạnh của đa diện.

2. Khái niệm về khối đa diện

Khôi đa diện là phần không gian được giới hạn bới một hình đa diện (H), kể cả hình đa diện đó.

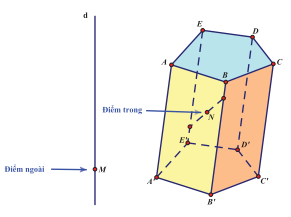
Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện. Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện giới hạn khối đa diện ấy được gọi là điểm trong của khối đa diện. Tập hợp các điểm trong được gọi là mîen trong, tập hợp các điểm ngoài được gọi là mîen ngoài khối đa diện.

Mỗi đa diện (H) chia các điểm còn lại của không gian thành hai miền không giao nhau: miền trong và miền ngoài của (H). Trong đó chỉ có duy nhất miền ngoài là chứa hoàn toàn một đường thẳng d nào đấy. Khối đa diện (H) là hợp của hình đa diện (H) và miền trong của nó.

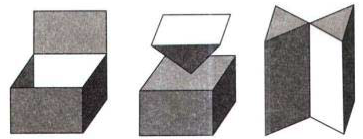
Ví dụ 1: Các hình dưới đây là những hình đa diện

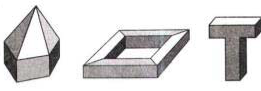
Ví dụ 2: Các hình dưới đây không là hình đa diện

II. Hai hình bẳng nhau

1. Phép dời hình trong không gian và sự bằng nhau giữa các khối đa diện.

- Trong không gian quy tắc đặt tương ứng mỗi điểm M với điểm \({M^\prime }\) xác định duy nhất được gọi là một phép biến hình trong không gian.

- Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giũa hai điểm tùy ý.

Nhận xét:

- Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.

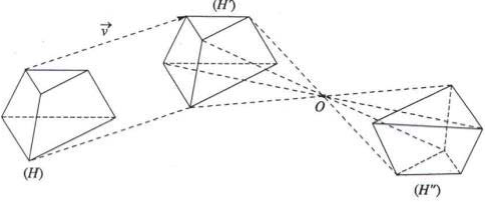
- Phép dời hình biến một đa diện thành (H) một đa diện  H', biến các đỉnh, cạnh, mặt của , đa diện (H) thành đỉnh, cạnh, mặt tương ứng của đa diện \(\left( {{{\rm{H}}^\prime }} \right)\).

a) Phép dời hình tịnh tiến theo vector v là phép biến hình biến điểm M thành \({{\rm{M}}^\prime }\) sao cho \(\overrightarrow {{M^\prime }}  = \vec v.\)

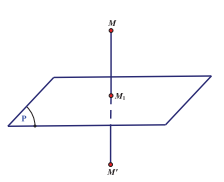
b) Phép đối xúng qua mặt phẳng (P) là phép biến hình biến mọi điểm thuộc (P) thành chính nó, biến điểm M không thuộc (P) thành điểm \({{\rm{M}}^\prime }\) sao cho (P) là mặt phẳng chung trực của \({\rm{M}}{{\rm{M}}^\prime }\). Nếu phép đối xứng qua mặt phẳng (P) biến hình (H) thành chính nó thì (P) được gọi là mặt phẳng đối xứng của (H).

c) Phép đối xúng tâm O là phép biến hình biến điểm O thành chính nó, biến điếm M khác O thành điểm \({{\rm{M}}^\prime }\) sao cho O là trung điểm của \({\rm{M}}{{\rm{M}}^\prime }\).

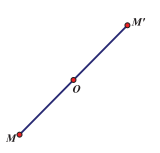
Nếu phép đối xứng tâm O biến hình (H) thành chính nó thì O được gọi là tâm đối xứng của (H).

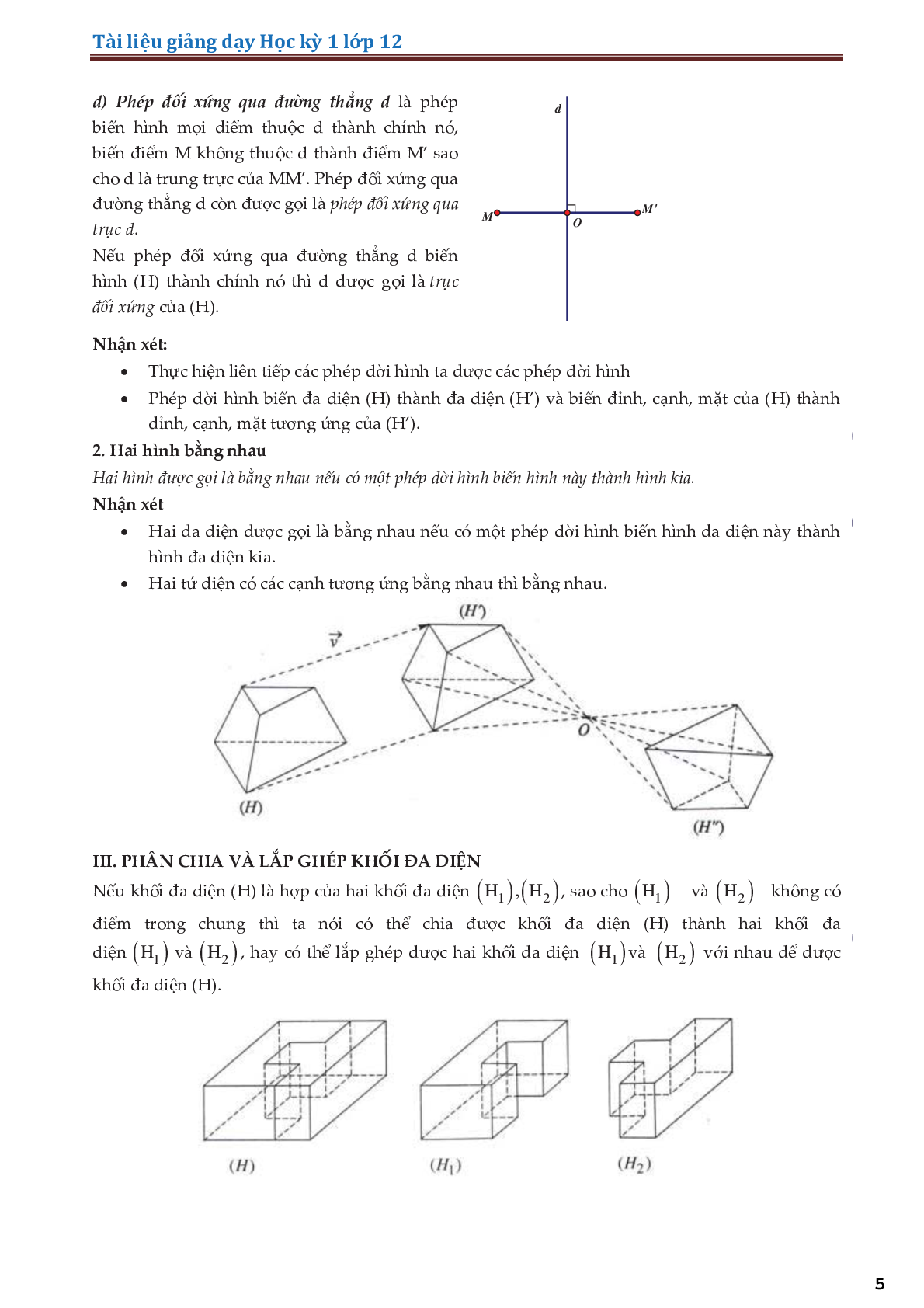
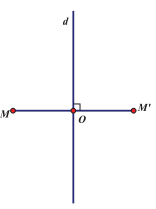
d) Phép đối xú́ng qua đường thẳng d là phép biến hình mọi điểm thuộc d thành chính nó, biến điểm M không thuộc d thành điểm \({M^\prime }\) sao cho d là trung trực của \({\rm{M}}{{\rm{M}}^\prime }\). Phép đối xứng qua đường thẳng d còn được gọi là phép đô̂i xúng qua trục d.

Nếu phép đối xứng qua đường thẳng d biến hình (H) thành chính nó thì d được gọi là trục đôi xúng của (H).

Nhận xét:

- Thực hiện liên tiếp các phép dời hình ta được các phép dời hình

- Phép dời hình biến đa diện (H) thành đa diện \(\left( {{{\rm{H}}^\prime }} \right)\) và biến đỉnh, cạnh, mặt của (H) thành đỉnh, cạnh, mặt tương ứng của \(\left( {{{\rm{H}}^\prime }} \right)\).

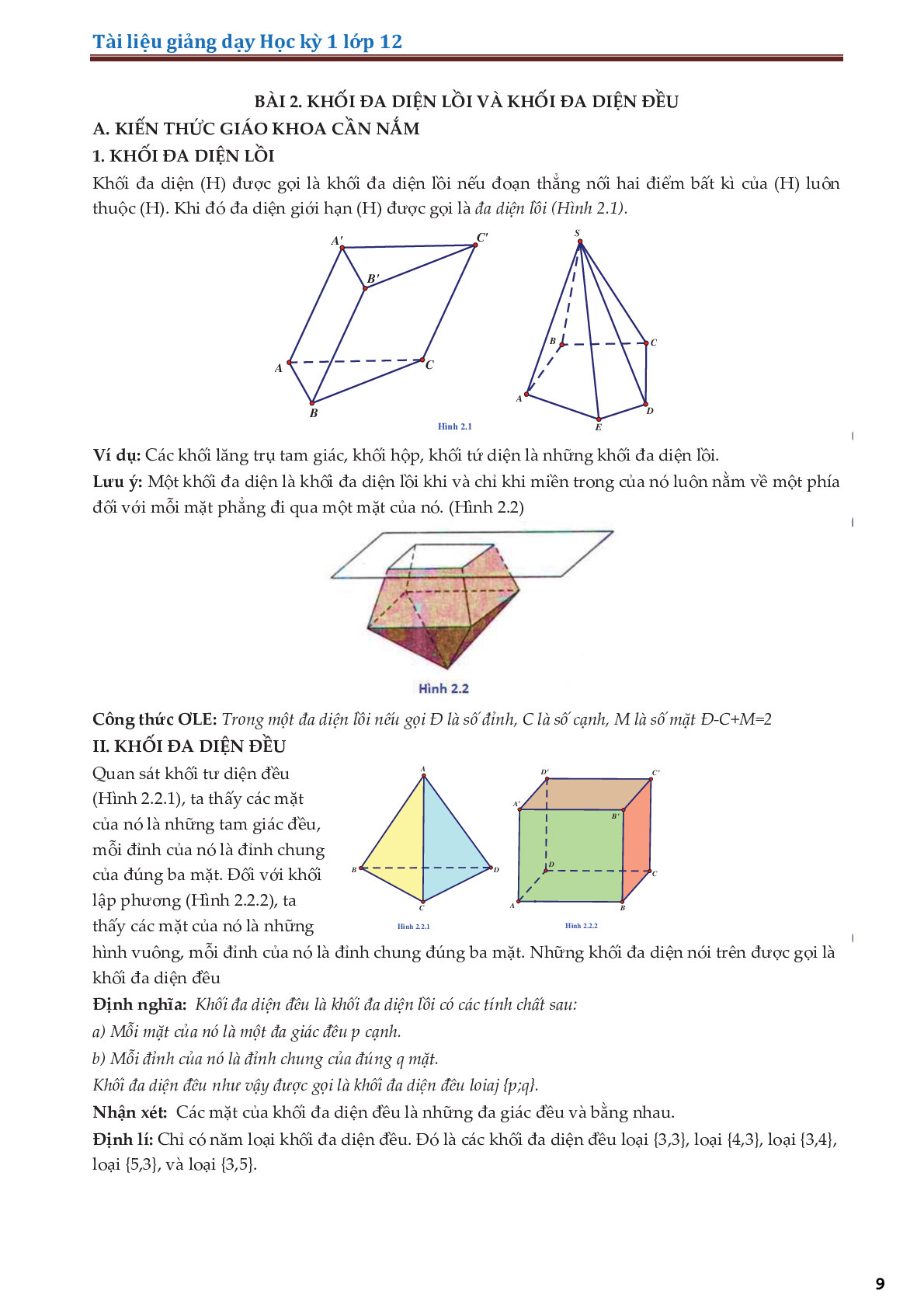
2. Hai hình bằng nhau

Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.

Nhận xét

- Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến hình đa diện này thành hình đa diện kia.

- Hai tứ diện có các cạnh tương ứng bằng nhau thì bằng nhau.

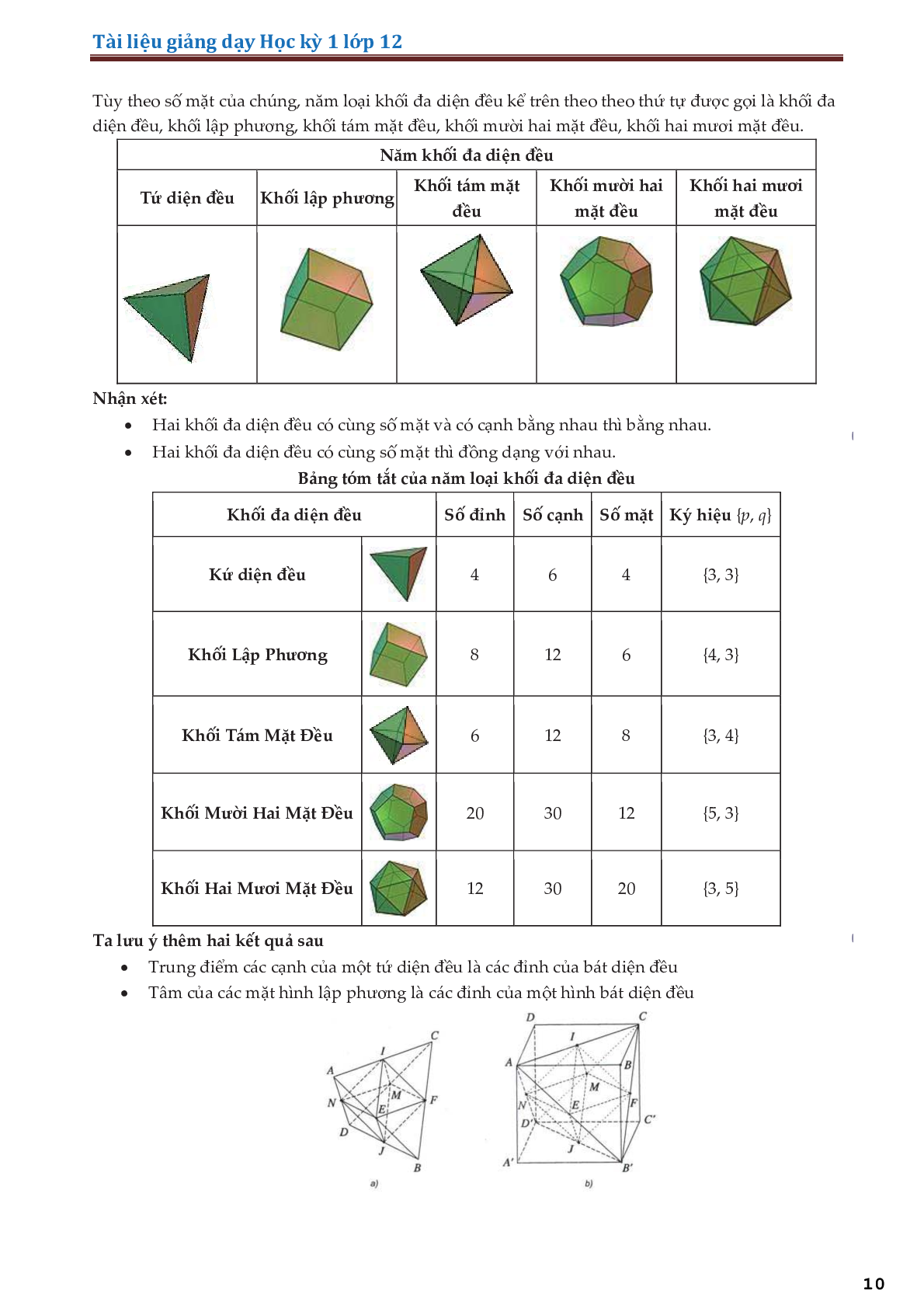
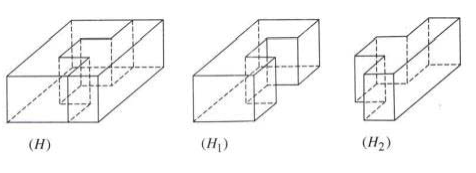
III. Phân chia và lắp ghép khối đa diện

Nếu khối đa diện (H) là hợp của hai khối đa diện \(\left( {{{\rm{H}}_1}} \right),\left( {{{\rm{H}}_2}} \right)\), sao cho \(\left( {{{\rm{H}}_1}} \right)\) và \(\left( {{{\rm{H}}_2}} \right)\) không có điểm trong chung thì ta nói có thể chia được khối đa diện (H) thành hai khối đa diện \(\left( {{{\rm{H}}_1}} \right)\) và \(\left( {{{\rm{H}}_2}} \right)\), hay có thể lắp ghép được hai khối đa diện \(\left( {{{\rm{H}}_1}} \right)\) và \(\left( {{{\rm{H}}_2}} \right)\) với nhau để được khối đa diện (H).

Ví dụ. Xét khối lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Mặt phẳng \(BD{D^\prime }{B^\prime }\) cắt khối lập phương đó theo một thiết diện là hình chữ nhật \({\rm{BD}}{{\rm{D}}^\prime }{{\rm{B}}^\prime }\). Thiết diện này chia các điểm còn lại của khối lập phương ra làm hai phần. Mỗi phần cùng với hình chữ nhật \({\rm{BD}}{{\rm{D}}^\prime }{{\rm{B}}^\prime }\) tạo thành khối lăng trụ, như vậy có hai khối lăng trụ: \(ABD \cdot {A^\prime }{B^\prime }{D^\prime }\) và \(BCD \cdot {B^\prime }{C^\prime }{D^\prime }\). Khi đó ta nói mặt phẳng (P) chia khối lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) thành hai khối lăng trụ \(ABD \cdot {A^\prime }{B^\prime }{D^\prime }\) và \(BCD \cdot {B^\prime }{C^\prime }{D^\prime }\).

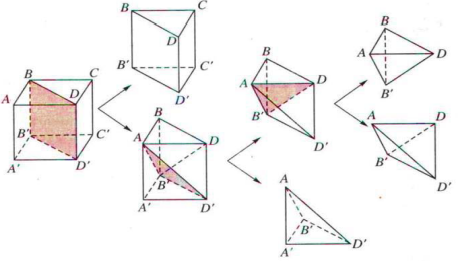
Tưong tự trên ta có thể chia tiếp khối trụ \({\rm{ABD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{D}}^\prime }\) thành ba khối tứ diện: \({\rm{ADB}}{{\rm{B}}^\prime },{\rm{AD}}{{\rm{B}}^\prime }{{\rm{D}}^\prime }\) và \({\rm{A}}{{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{D}}^\prime }\).

Nhận xét: Một khối đa diện bất kì luôn có thể phân chia được thành các khối tứ diện.

B. Câu hỏi và bài tập trắc nghiệm khách quan

Câu 1: Cho khối lăng trụ tam giác đều ABC.A 'B' \({C^\prime }\). Về phía ngoài khối lăng trụ này ta ghép thêm một khối lăng trụ tam giác đều bằng với khối lăng trụ đã cho, sao cho hai khối lăng trụ có chung một mặt bên. Hỏi khối đa diện mới lập thành có mấy cạnh?

A. 9 .

B. 12 .

C. 15 .

D. 18 .

Câu 2: Cho khối chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Về phía ngoài khối chóp này ta ghép thêm một khối chóp tứ diện đều có cạnh bằng a, sao cho một mặt của khối tứ diện đều trùng với một mặt của khối chóp đã cho. Hỏi khối đa diện mới lập thành có mấy mặt?

A. 5 .

B. 6 .

C. 7 .

D. 9 .

Câu 3: Tứ diện đều có mấy mặt phẳng đối xứng

A. 0 .

B. 4 .

C. 6 .

D. 2 .

Câu 4: Hình lập phương có mấy mặt phẳng đối xứng ?

A. 6 .

B. 7 .

C. 8 .

D. 9 .

Câu 5: Số mặt phẳng đối xứng của hình bát diện đều là:

A. 6 .

B. 7 .

C. 8 .

D. 9 .

Câu 6: Trong không gian cho hai vectơ \(\vec u\) và \(\vec v\). Với M là điểm bất kỳ, ta gọi \({M_1}\) là ảnh của M qua phép \({{\rm{T}}_{\overrightarrow {\rm{u}} }}\) và \({{\rm{M}}_2}\) là ảnh của \({{\rm{M}}_1}\) qua phép \({{\rm{T}}_{\overrightarrow {\rm{v}} }}\),. Khi đó phép biến hình biến điểm M thành đểm \({{\rm{M}}_2}\) là:

A. Phép tịnh tiến theo vecto \(\vec u + \vec v\quad \)

B. Phép tịnh tiến theo vecto \(\vec u\)

C. Phép tịnh tiến theo vecto \(\vec v\)

D. Một phép biến hình khác

Câu 7: Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó?

A. Không có .

B. 1 .

C. 2 .

D. Vô số .