Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tóm tắt lý thuyết và bài tập trắc nghiệm phương trình mặt cầu, tài liệu bao gồm 49 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tóm tắt lý thuyết và bài tập trắc nghiệm phương trình mặt cầu

Chủ đề 2. Phương trình mặt cầu

A. Kiến thức cơ bản

1. Định nghĩa

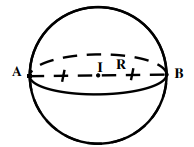
Cho điểm I cố định và một số thực dương R. Tập hợp tất cả những điểm M trong không gian cách I một khoảng R được gọi là mặt cầu tâm I, bán kính R.

Kí hiệu: \[S(I;R) \Rightarrow S(I;R) = \{ M/IM = R\} \]

Dạng 1: Phương trình chính tắc

Mặt cầu (S) có tâm I (a;b;c), bán kính R > 0.

\[(S):{(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\]  (1)

Dạng 2: Phương trình tổng quát

\[(S):{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\]   (2)

\[ \Rightarrow \]Điều kiện để phương trình (2) là phương trình mặt cầu: \[{a^2} + {b^2} + {c^2} - d > 0\]

(S) có tâm I (a;b;c)

(S) có bán kính : \[R = \sqrt {{a^2} + {b^2} + {c^2} - d} \]

3. Vị trí tương đối giữa mặt cầu và mặt phẳng:

Cho mặt cầu S(I;R) và mặt phẳng (P).Gọi H là hình chiếu vuông góc của I lên (P) \[ \Rightarrow d = IH\]là khoảng cách từ I đến mặt phẳng (P). Khi đó:

- Nếu d > R: Mặt cầu và mặt phẳng không có điểm chung.

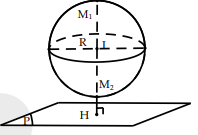
- Nếu d = R: Mặt phẳng tiếp xúc mặt cầu. Lúc đó (P) là mặt phẳng tiếp diện của mặt cầu và H là tiếp điểm.

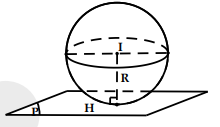
- Nếu d < R: Mặt phẳng (P) cắt mặt cầu theo thiết diện là đường tròn có tâm I’ và bán kính \[r = \sqrt {{R^2} - I{H^2}} \]

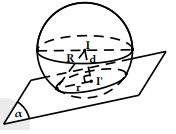
Lưu ý: Khi mặt phẳng (P) đi qua tâm I thì mặt phẳng (P) được gọi là mặt phẳng kính và thiết diện lúc đó được gọi là đường tròn lớn.

4. Vị trí tương đối giữa mặt cầu và đường thẳng:

Cho mặt cầu S (I;R) và đường thẳng ∆. Gọi H là hình chiếu của I lên ∆. Khi đó:

- IH > R: ∆ không cắt mặt cầu.

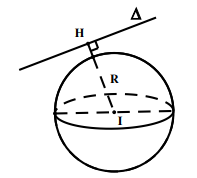
- IH = R : ∆ tiếp xúc với mặt cầu. ∆ là tiếp tuyến của (S) và H là tiếp điểm.

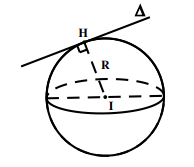
- IH < R : ∆ cắt mặt cầu tại hai điểm phân biệt.

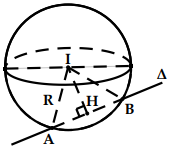
* Lưu ý: Trong trường hợp ∆ cắt (S) tại 2 điểm A, B thì bán kính R của (S) được tính như sau:

Xác định: \[d\left( {I;\Delta } \right) = IH\]

Lúc đó: \[R = \sqrt {I{H^2} + A{H^2}}  = \sqrt {I{H^2} + {{\left( {\frac{{AB}}{2}} \right)}^2}} \]

Đường tròn trong không gian Oxyz

Đường tròn (C) trong không gian Oxyz, được xem là giao tuyến của (S) và mặt phẳng (α)

\[(S):{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\]

\[(\alpha ):Ax + By + Cz + D = 0\]

Xác định tâm I’ và bán kính R’ của (C).

Tâm I’ = d ∩ (α).

Trong đó d là đường thẳng đi qua I và vuông góc với mp (α)

Bán kính \[R' = \sqrt {{R^2} + {{(II')}^2}}  = \sqrt {{R^2} + {{\left[ {d\left( {I;(\alpha )} \right)} \right]}^2}} \]

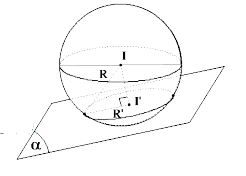
5. Điều kiện tiếp xúc : Cho mặt cầu (S) tâm I, bán kính R.

Đường thẳng ∆ là tiếp tuyến của (S) ⇔ \[d\left( {I;\Delta } \right) = R\].

Mặt phẳng (α) là tiếp diện của (S) ⇔ \[d\left( {I;(\alpha )} \right) = R\]

Lưu ý: Tìm tiếp điểm M₀(x₀;y₀;z₀).

Sử dụng tính chất : \[\left[ {\begin{array}{*{20}{c}}{I{M_0} \bot d}\\{I{M_0} \bot (\alpha )}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{{\overrightarrow {IM} }_0} \bot \overrightarrow {{a_d}} }\\{\overrightarrow {I{M_0}}  \bot \overrightarrow {{n_\alpha }} }\end{array}} \right.\]

B. Kỹ năng cơ bản

Dạng 1: Viết phương trình mặt cầu

Phương pháp:

Thuật toán 1: Bước 1: Xác định tâm I(a;b;c).

Bước 2: Xác định bán kính R của (S).

Bước 3: Mặt cầu (S) có tâm I(a;b;c) và bán kính R .

\[(S):{(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\]

Thuật toán 2: Gọi phương trình \[(S):{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\]

Phương trình (S) hoàn toàn xác định nếu biết được a, b, c, d (\[{a^2} + {b^2} + {c^2} - d > 0\])

Bài tập 1 : Viết phương trình mặt cầu (S), trong các trường hợp sau:

a) (S ) có tâm I (2;2; −3) và bán kính R = 3.

b) (S ) có tâm I (1;2;0) và (S) qua P(2; −2;1).

c) (S ) có đường kính AB với A(1;3;1), B(−2;0;1).

Bài giải:

a) Mặt cầu tâm I (2;2; −3) và bán kính R = 3, có phương trình:

\[(S):{(x - 2)^2} + {(y - 2)^2} + {(z + 3)^2} = 9\]

b) Ta có: \[\overrightarrow {IP}  = (1; - 4;1) \Rightarrow IP = 3\sqrt 2 \].

Mặt cầu tâm I (1;2;0) và bán kính \[R = IP = 3\sqrt 2 \], có phương trình:

\[(S):{(x - 1)^2} + {(y - 2)^2} + {z^2} = 18\]

c) Ta có: \[\overrightarrow {AB}  = ( - 3; - 3;0) \Rightarrow AB = 3\sqrt 2 \]

Gọi I là trung điểm AB ⇒ \[I\left( { - \frac{1}{2};\frac{3}{2};1} \right)\].

Mặt cầu tâm \[I\left( { - \frac{1}{2};\frac{3}{2};1} \right)\] và bán kính \[R = \frac{{AB}}{2} = \frac{{3\sqrt 2 }}{2}\], có phương trình:

\[(S):{(x + \frac{1}{2})^2} + {(y - \frac{3}{2})^2} + {(z - 1)^2} = \frac{9}{2}\]

Bài tập 2 : Viết phương trình mặt cầu (S), trong các trường hợp sau:

a) (S) qua A(3;1;0), B(5;5;0) và tâm I thuộc trục Ox .

b) (S) có tâm O và tiếp xúc mặt phẳng (α): 16x – 15y – 12z + 75 = 0.

c) (S) có tâm I (−1;2;0) và có một tiếp tuyến là đường thẳng ∆:  \[\frac{{x + 1}}{{ - 1}} = \frac{{y - 1}}{1} = \frac{z}{{ - 3}}\]

Bài giải: a) Gọi I(a;0;0) ∈ Ox. Ta có : \[\overrightarrow {IA}  = (3 - a;1;0),\overrightarrow {IB}  = (5 - a;5;0)\]

Do (S) đi qua A, B

 ⇔ \[IA = IB \Leftrightarrow \sqrt {{{(3 - a)}^2} + 1}  = \sqrt {{{(5 - a)}^2} + 25} \]

\[ \Leftrightarrow 4a = 40 \Leftrightarrow a = 10\]

 ⇒ I (10;0;0) và IA = \[5\sqrt 2 \].

Mặt cầu tâm I (10;0;0) và bán kính R = \[5\sqrt 2 \], có phương trình

(S): \[(S):{(x - 10)^2} + {y^2} + {z^2} = 50\]

b) Do (S) tiếp xúc với (α) ⇔ \[d\left( {O,(\alpha )} \right) = R \Leftrightarrow R = \frac{{75}}{{25}} = 3\]

Mặt cầu tâm O(0;0;0) và bán kính R = 3, có phương trình \[(S):{x^2} + {y^2} + {z^2} = 9\]

c) Chọn A (−1;1;0) ∈ ∆ ⇒ \[\overrightarrow {IA}  = (0; - 1;0)\].

Đường thẳng ∆ có một vectơ chỉ phương là \[\overrightarrow {{u_\Delta }}  = ( - 1;1; - 3)\].

Ta có: \[\left[ {\overrightarrow {IA} ,\overrightarrow {{u_\Delta }} } \right] = (3;0; - 1)\].

Do (S) tiếp xúc với ∆ ⇔ \[d\left( {I,\Delta } \right) = R\]

\[ \Leftrightarrow R = \frac{{\left| {\left[ {\overrightarrow {IA} ,\overrightarrow {{u_\Delta }} } \right]} \right|}}{{\left| {\overrightarrow {{u_\Delta }} } \right|}} = \frac{{\sqrt {10} }}{{11}}\].

Mặt cầu tâm I (−1;2;0) và bán kính \[R = \frac{{\sqrt {10} }}{{11}}\], có phương trình

\[(S):{(x + 1)^2} + {(y - 2)^2} + {z^2} = \frac{{10}}{{121}}\]

Bài tập 3 : Viết phương trình mặt cầu (S) biết :

a) (S) qua bốn điểm A(1;2; −4), B(1; −3;1), C(2;2;3), D(1;0;4) .

b) (S) qua A(0;8;0), B(4;6;2), C(0;12;4) và có tâm I thuộc mặt phẳng (Oyz).

Bài giải:

a) Cách 1: Gọi I(x;y;z) là tâm mặt cầu (S) cần tìm.

Theo giả thiết:

\[\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{IA = IB}\\{IA = IC}\\{IA = ID}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{I{A^2} = I{B^2}}\\{I{A^2} = I{C^2}}\\{I{A^2} = I{D^2}}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - y + z =  - 1}\\{x + 7z =  - 2}\\{y - 4z = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x =  - 2}\\{y = 1}\\{z = 0}\end{array}} \right.\end{array}\]

Do đó: I (−2;1;0) và R = IA = \[\sqrt {26} \].

Vậy \[(S):{(x + 2)^2} + {(y - 1)^2} + {z^2} = 26\].

Cách 2: Gọi phương trình mặt cầu

\[(S):{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\],

(\[{a^2} + {b^2} + {c^2} - d > 0\])

Do A(1;2; −4) ∈ (S) ⇔ – 2a – 4b + 8c + d = 0 (1)

Tương tự: B(1; −3;1) ∈ (S) ⇔ – 2a + 6b – 2c + d = 11 (2)

C (2;2;3) ∈ (S) ⇔ – 4a – 4b – 6c + d = - 17 (3)

D (1;0;4) ∈ (S) ⇔ – 2a – 8c + d = - 17  (4)

Giải hệ (1), (2), (3), (4) ta có a, b, c, d suy ra phương trình mặt cầu

\[(S):{(x + 2)^2} + {(y - 1)^2} + {z^2} = 26\]

b) Do tâm I của mặt cầu nằm trên mặt phẳng (Oyz) ⇒ I (0;b;c).

Ta có: \[IA = IB = IC\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{I{A^2} = I{B^2}}\\{I{A^2} = I{C^2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{b = 7}\\{c = 5}\end{array}} \right.} \right.\]

Vậy I (0;7;5) và R = \[\sqrt {26} \]. Vậy \[(S):{x^2} + {(y - 7)^2} + {(z - 5)^2} = 26\].

Bài tập 4: Viết phương trình mặt cầu (S) có tâm I thuộc đường thẳng ∆: \[\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y =  - 1}\\{z =  - t}\end{array}} \right.\] và (S) tiếp xúc với hai mặt phẳng (α): \[x + 2y + 2z + 3 = 0\] và (β): \[x + 2y + 2z + 7 = 0\].

Bài giải: Gọi I (t;−1;−t) ∈ ∆ là tâm mặt cầu (S) cần tìm.

Theo giả thiết: \[d\left( {I,(\alpha )} \right) = d\left( {I,(\beta )} \right)\]

\[ \Leftrightarrow \frac{{\left| {1 - t} \right|}}{3} = \frac{{\left| {5 - t} \right|}}{3} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{1 - t = 5 - t}\\{1 - t = t - 5}\end{array} \Rightarrow t = 3} \right.\]

Suy ra: I (3;−1;−3) và \[R = d\left( {I,(\alpha )} \right) = \frac{2}{3}\].

Vậy \[(S):{(x - 3)^2} + {(y + 1)^2} + {(z + 3)^2} = \frac{4}{9}\].

Bài tập 5: Lập phương trình mặt cầu (S) qua 2 điểm A(2;6;0), B(4;0;8) và có tâm thuộc d: \[\frac{{x - 1}}{{ - 1}} = \frac{y}{2} = \frac{{z + 5}}{1}\].

Bài giải:

Ta có d: \[\left\{ {\begin{array}{*{20}{c}}{x = 1 - t}\\{y = 2t}\\{z =  - 5 + t}\end{array}} \right.\]. Gọi I (1-t;2t;-5+t) ∈ d là tâm của mặt cầu (S) cần tìm.

Ta có: \[\overrightarrow {IA}  = (1 + t;6 - 2t;5 - t),\overrightarrow {IB}  = (3 + t; - 2t;13 - t)\]

Theo giả thiết, do (S) đi qua A, B ⇔ AI = BI

\[ \Leftrightarrow \sqrt {{{(1 + t)}^2} + {{(6 - 2t)}^2} + {{(5 - t)}^2}}  = \sqrt {{{(3 + t)}^2} + 4{t^2} + {{(13 - t)}^2}} \]

\[ \Leftrightarrow 62 - 32t = 187 - 20t \Leftrightarrow 12t =  - 116 \Leftrightarrow t =  - \frac{{29}}{3}\]

\[ \Rightarrow I\left( {\frac{{32}}{3}; - \frac{{58}}{3}; - \frac{{44}}{3}} \right)\] và R = IA = \[2\sqrt {233} \] .

Vậy (S): \[(S):{(x - \frac{{32}}{3})^2} + {(y + \frac{{58}}{3})^2} + {(z + \frac{{44}}{3})^2} = 932\].

Bài tập 6: Viết phương trình mặt cầu (S) có tâm I (2;3; −1) và cắt đường thẳng ∆:\[\frac{{x + 1}}{1} = \frac{{y - 1}}{{ - 4}} = \frac{z}{1}\] tại hai điểm A, B với AB =16 .

Bài giải: Chọn M(−1;1;0) ∈ ∆ ⇒  \[\overrightarrow {IM}  = ( - 3; - 2;1)\]

Đường thẳng ∆ có một vectơ chỉ phương là \[\overrightarrow {{u_\Delta }}  = (1; - 4;1)\].

Ta có:

\[\begin{array}{l}\left[ {\overrightarrow {IM} ,\overrightarrow {{u_\Delta }} } \right] = (2;4;14)\\ \Rightarrow d(I,\Delta ) = \frac{{\left| {\left[ {\overrightarrow {IM} ,\overrightarrow {{u_\Delta }} } \right]} \right|}}{{\left| {\overrightarrow {{u_\Delta }} } \right|}} = 2\sqrt 3 \end{array}\]

Gọi R là bán kính mặt cầu (S).

Theo giả thiết :

\[R = \sqrt {{{\left[ {d(I,\Delta )} \right]}^2} + \frac{{A{B^2}}}{4}}  = 2\sqrt {19} \]

Vậy \[(S):{(x - 2)^2} + {(y - 3)^2} + {(z + 1)^2} = 76\]

Bài tập 7: Cho hai mặt phẳng (P): 5x – 4y + z – 6 = 0, (Q): 2x – y + z + 7 = 0 và đường thẳng ∆:  \[\frac{{x - 1}}{7} = \frac{y}{3} = \frac{{z - 1}}{{ - 2}}\]. Viết phương trình mặt cầu (S) có tâm I là giao điểm của (P) và ∆ sao cho (Q) cắt (S) theo một hình tròn có diện tích là 20π .

Bài giải: Ta có ∆:\[\left\{ {\begin{array}{*{20}{c}}{x = 1 + 7t}\\{y = 3t}\\{z = 1 - 2t}\end{array}} \right.\]. Tọa độ I là nghiệm của hệ phương trình: \[\left\{ {\begin{array}{*{20}{c}}{x = 1 + 7t;(1)}\\{y = 3t;(2)}\\{z = 1 - 2t;(3)}\\{5x - 4y + z - 6 = 0;(4)}\end{array}} \right.\]

Thay (1), (2), (3) vào (4) ta có:

\[\begin{array}{l}5(1 + 7t) - 4(3t) + (1 - 2t) - 6 = 0\\ \Leftrightarrow t = 0 \Rightarrow I(1;0;1)\end{array}\]

Ta có: \[d\left( {I,(Q)} \right) = \frac{{5\sqrt 6 }}{3}\]