Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề phương pháp tọa độ hóa hình không gian, tài liệu bao gồm 52 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Chuyên đề phương pháp tọa độ hóa hình không gian

PHƯƠNG PHÁP TỌA ĐỘ HÓA HÌNH CỔ ĐIỂN

Đôi khi trong giải toán hình học không gian cổ điển ta sẽ gặp khá nhiều bài toán tính toán phức tạp, tuy nhiên trong phòng thi ta lại không có nhiều thời gian, vì thế trong chương này chúng ta sẽ tìm hiểu một phương pháp giải quyết nhanh các bài toán tính toán phức tạp và khó trong hình không gian cổ điển, liên quan tới cực trị, góc, khoảng cách.

I. Ý tưởng.

Phương pháp

Trên mạng có một vài tài liệu nói về phương pháp này và chia thành rất nhiều dạng, điều đó làm chúng ta khi áp dụng có phần khó nhớ và máy móc, tuy nhiên chúng ta chỉ cần nắm được dấu hiệu và phương pháp sau

Bước 1. Chọn hệ trục tọa độ. Trong bước này ta sẽ xác định 3 đường vuông góc có trong bài toán và gọi đó là 3 đường cơ sở. Thông thường thì ta sẽ quy ước trục Ox hướng vào mình, trục Oz nằm ngang, còn lại là trục Oy

Bước 2. Xác định tọa độ các điểm liên trên hình liên quan tới bài toán. Với những bạn chưa quen thì chúng ta xác định tọa độ hình chiếu của điểm cần tìm lên các trục, từ đó sẽ suy ra được tọa độ điểm cần tính.

Bước 3. Áp dụng công thức.

Sau đây chúng ta sẽ nhắc lại một số công thức cần nhớ trong phần này. Diện tích và thể tích

Diện tích tam giác ABC: \[S = \frac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right|\]

Thể tích tứ diện ABCD: \[V = \frac{1}{6}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} } \right|\]

Thể tích hình hộp ABCD.A’B’C’D’: \[V = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AA'} } \right|\]

Thể tích hình lăng trụ ABC,A’B’C’: \[V = \frac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AA'} } \right|\]

Góc giữa 2 mặt phẳng: Mặt phẳng (P) có vecto pháp tuyến \[\overrightarrow n \] và mặt phẳng (Q) có vecto pháp tuyến \[\overrightarrow {n'} \] thì \[\cos \left( {(P),(Q)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right|\]

Góc giữa 2 đường thẳng: Đường thẳng d có VTCP \[\overrightarrow u \] và d’ có VTCP \[\overrightarrow v \] thì

\[\cos (d,d') = \left| {\cos \left( {\overrightarrow u ,\overrightarrow v } \right)} \right|\]

Góc giữa đường thẳng và mặt phẳng: Đường thẳng d có VTCP \[\overrightarrow u \] và (P) có VTPT \[\overrightarrow n \] thì \[\sin (d,(P)) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right|\]

Khoảng cách từ M₀ (x₀;y₀;z₀) đến mặt phẳng:

(Oxy) là |z₀|; (Oyz) là |x₀|; (Oxz) là |y₀|

(P): \[Ax + By + Cz + D = 0\]là \[d\left( {{M_0},P} \right) = \frac{{\left| {Ax + By + Cz + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\]

Khoảng cách từ một điểm đến 1 đường thẳng:

Cho M (x₀;y₀;z₀) và đường thẳng d qua A và có vectơ chỉ phương \[\overrightarrow u  = \overrightarrow {AB} \] thì

\[d\left( {{M_0},d} \right) = \frac{{\left| {\left[ {\overrightarrow {A{M_0}} ,\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}}\]

Khoảng cách giữa hai đường thẳng chéo nhau: Đường thẳng d₁ qua M₁ và có VTCP \[\overrightarrow {{u_1}} \]; d₂ qua M₂ và có VTCP thì \[d\left( {{d_1},{d_2}} \right) = \frac{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}} } \right|}}{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right]} \right|}}\]

Chú ý. Thông thường các bài mà không có 3 đường vuông góc thì ta sẽ phải tự dựng thêm để gắn tọa độ và những bài liên quan tới hình lập phương, hình hộp chữ nhật, chối chóp có 3 đường vuông góc, lăng trụ đứng thì khi áp dụng phương pháp này sẽ giải rất nhanh !

II. Các bài toán

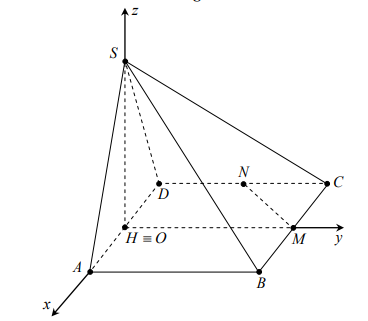
Câu 1. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N lần lượt là trung điểm của BC và CD. Tính bán kính R của khối cầu ngoại tiếp khối chóp S.CMN.

Lời giải

Chọn hệ trục Oxyz như hình vẽ và xét a =1.

Khi đó H º O, \[M(0;1;0),C\left( { - \frac{1}{2};1;0} \right),N\left( { - \frac{1}{2};\frac{1}{2};0} \right),S\left( {0;0;\frac{{\sqrt 3 }}{2}} \right)\]

Phương trình mặt cầu ngoại tiếp chóp S.CMN có dạng

\[(S):{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\], (\[{a^2} + {b^2} + {c^2} - d > 0\])

S, C, M, N Î (S ) nên ta có hệ phương trình

\[\left\{ {\begin{array}{*{20}{c}}{ - 2b + d =  - 1}\\{a - 2b + d =  - \frac{5}{4}}\\{a - b + d =  - \frac{1}{2}}\\{ - \sqrt 3 c + d =  - \frac{3}{4}}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{a =  - \frac{1}{4}}\\{b = \frac{3}{4}}\\{c = \frac{{5\sqrt 3 }}{{12}}}\\{d = \frac{1}{2}}\end{array}} \right.\]

Ta có \[{a^2} + {b^2} + {c^2} - d = \frac{{31}}{{48}}\] hay \[\sqrt {{a^2} + {b^2} + {c^2} - d}  = \frac{{\sqrt {93} }}{{12}}\]

Vậy \[R = \frac{{\sqrt {93} }}{{12}}\].

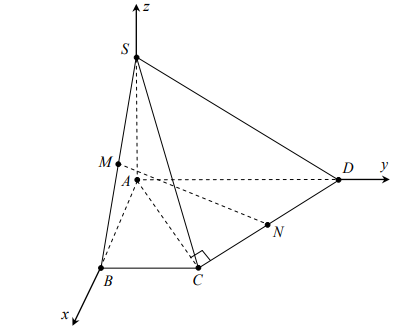
Câu 2. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, thỏa mãn điều kiện AB = BC = a, AD a = 2, SA vuông góc với mặt đáy (ABCD), SA = a. Gọi M, N lần lượt là trung điểm của SB, CD. Tính cosin của góc giữa MN và (SAC) .

Lời giải

Chọn hệ trục như hình vẽ, chọn đơn vị là a

Có \[A(0;0;0),B(1;0;0),C(1;1;0),D(0;2;0),S(0;0;1),M\left( {\frac{1}{2};0;\frac{1}{2}} \right),N\left( {\frac{1}{2};\frac{3}{2};0} \right)\]

Vec tơ chỉ phương của MN là \[2\overrightarrow {MN}  = 2\left( {0;\frac{3}{2}; - \frac{1}{2}} \right) = (0;3; - 1)\].

Vec tơ pháp tuyến của (SAC) là \[\overrightarrow n  = \left[ {\overrightarrow {AC} ;\overrightarrow {AS} } \right] = (1; - 1;0)\].

Vậy \[\sin \left( {MN;(SAC)} \right) = \frac{{|3|}}{{\sqrt {9 + 1\sqrt 2 } }} = \frac{{3\sqrt 5 }}{{10}}\].

Suy ra\[\cos \left( {MN;(SAC)} \right) = \sqrt {1 - {{\left( {\frac{{3\sqrt 5 }}{{10}}} \right)}^2}}  = \frac{{\sqrt {55} }}{{10}}\].

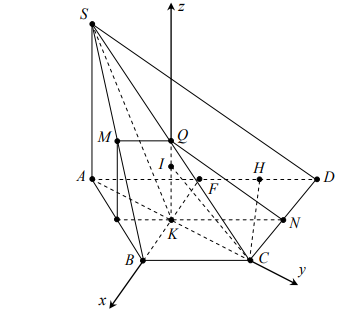
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD = 2AB = 2BC = 2CD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Gọi M, N lần lượt là trung điểm của SB và CD. Tính cosin góc giữa MN và (SAC), biết thể tích khối chóp S.ABCD bằng

Lời giải

 Vì ABCD là hình thang cân có AD = 2AB = 2BC = 2CD = 2a

Þ AD = 2a; AB = BC = CD = a Þ \[CH = \frac{{a\sqrt 3 }}{2}\];

\[{S_{ABCD}} = \frac{{a + 2a}}{2}.\frac{{a\sqrt 3 }}{2} = \frac{{3\sqrt 3 {a^2}}}{4}\]

Nên \[{V_{ABCD}} = \frac{1}{3}.\frac{{3\sqrt 3 {a^2}}}{4}.SA = \frac{{{a^3}\sqrt 3 }}{4} \Rightarrow SA = a\]

Gắn hình chóp vào hệ trục tọa độ như hình vẽ

Ta có \[K(0;0;0),B\left( {\frac{a}{2};0;0} \right),C\left( {0;\frac{{a\sqrt 3 }}{2};0} \right),A\left( {0; - \frac{{a\sqrt 3 }}{2};0} \right),N\left( {\frac{{ - a}}{2};\frac{{a\sqrt 3 }}{2};0} \right)\]

\[S\left( {0; - \frac{{a\sqrt 3 }}{2};a} \right),M\left( {\frac{a}{4}; - \frac{{a\sqrt 3 }}{4};\frac{a}{2}} \right)\].

\[\overrightarrow {MN}  = \left( {\frac{{ - 3a}}{4};\frac{{3a\sqrt 3 }}{4};\frac{{ - a}}{2}} \right)\].

Chọn \[\overrightarrow {{u_1}}  = ( - 3;3\sqrt 3 ; - 2)\]cùng phương với \[\overrightarrow {MN} \]

Nhận xét \[\left\{ {\begin{array}{*{20}{c}}{BK \bot SA}\\{BK \bot AC}\end{array}} \right. \Rightarrow BK \bot (SAC)\]

\[\overrightarrow {BK}  = \left( {\frac{a}{2};0;0} \right)\] là vtpt của (SAC). Chọn \[\overrightarrow {{n_1}}  = (1;0;0)\]cùng phương với \[\overrightarrow {BK} \].

Gọi \[\alpha \] là góc giữa MN và (SAC). Ta có \[\sin \alpha  = \frac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{n_1}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{n_1}} } \right|}} = \frac{{3\sqrt {10} }}{{20}} \Rightarrow \cos \alpha  = \frac{{\sqrt {310} }}{{20}}\].

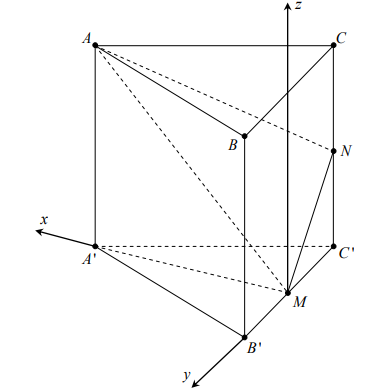
Câu 4. Cho hình lăng trụ đứng ABC. A’B’C’ có AB = AC = a, BAC = 120⁰, AA’ = a. Gọi M, N lần lượt là trung điểm của B’C¢ và CC¢. Số đo góc giữa mặt phẳng  AMN ) và mặt phẳng (ABC) bằng

Lời giải

Thiết lập hệ tọa độ Oxyz trong không gian như hình vẽ, gốc tọa độ O trùng M.

Dễ dàng tính được MB’ = MC’ = \[\frac{{a\sqrt 3 }}{2}\]; MA’ = \[\frac{a}{2}\].

M (0;0;0), N \[ \in \] (Oyz) \[ \Rightarrow N\left( {0; - \frac{{a\sqrt 3 }}{2};\frac{a}{2}} \right)\]

A \[ \in \](Oxz) \[ \Rightarrow A\left( {\frac{1}{2};0;a} \right)\]. Mp (ABC) // (A’B’C’);  (A’B’C’) \[ \equiv \] (Oxy)

\[ \Rightarrow \](ABC) có một vec tơ pháp tuyến là \[\overrightarrow k  = (0;0;1)\]

Ta có \[\overrightarrow {MA}  = (\frac{a}{2};0;0)\]cùng phương \[\overrightarrow {{u_1}}  = (1;0;2)\]

\[\overrightarrow {MN}  = (0; - \frac{{a\sqrt 3 }}{2};\frac{a}{2})\]cùng phương \[\overrightarrow {{u_2}}  = (0; - \sqrt 3 ;1)\]

\[ \Rightarrow \](AMN) có một véc tơ pháp tuyến \[\overrightarrow n  = \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = (2\sqrt 3 ; - 1; - \sqrt 3 )\]

\[ \Rightarrow \cos \left( {(AMN),(ABC)} \right) = \left| {\cos \left( {\overrightarrow k ,\overrightarrow n } \right)} \right| = \frac{{\sqrt 3 }}{4}\]