Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Ứng dụng phương pháp tọa độ để giải bài toán hình học không gian - bản 2, tài liệu bao gồm 47 trang, 50 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Ứng dụng phương pháp tọa độ để giải bài toán hình học không gian - bản 2

Ứng dụng phương pháp tọa độ để giải toán hình học không gian

1. Phương pháp

Bước 1: Chọn hệ trục tọa độ Oxyz trong không gian: Vì Ox, Oy, Oz vuông góc với nhau từng đôi một nên nếu hình vẽ bài toán cho có chứa các cạnh vuông góc thì ta ưu tiên chọn các cạnh đó làm trục tọa độ.

Bước 2: Suy ra tọa độ của các đỉnh, điểm trên hệ trục tọa độ vừa ghép.

Bước 3: Sử dụng các kiến thức về tọa độ không gian để giải quyết bài toán

2. Các bài toán ghép trục tọa độ thường gặp và cách suy ra tọa độ các đỉnh

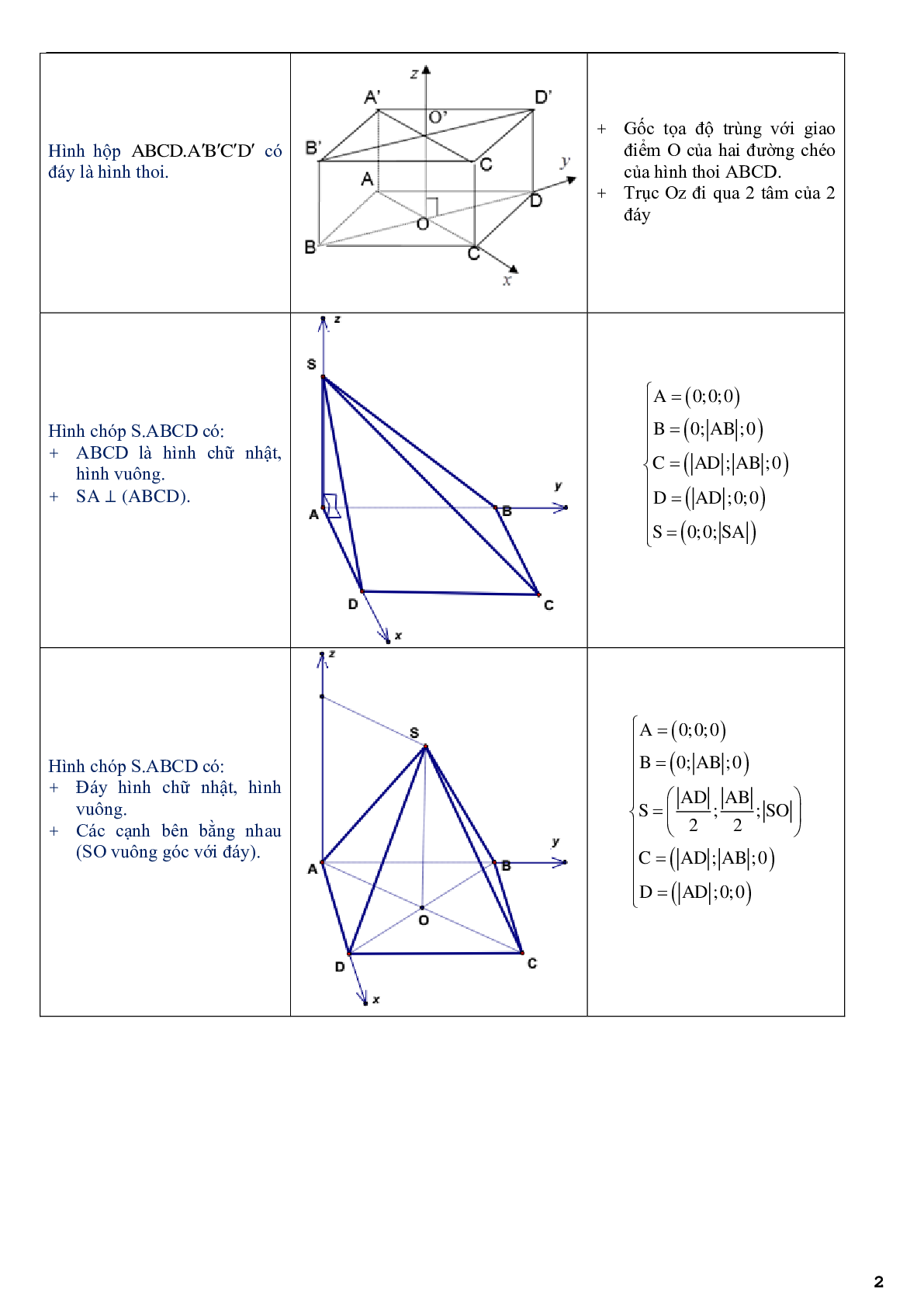
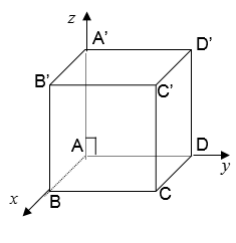
a. Hình lập phương hoặc hình hộp chữ nhật ABCD.A¢B¢C¢D¢

- Tọa độ các điểm:

Với hình lập phương:

\[\left\{ {\begin{array}{*{20}{c}}{A(0;0;0),B(a;0;0)}\\{C(a;a;0),D(0;a;0)}\\{A'(0;0;a),B'(a;0;a)}\\{C'(a;a;0),D'(0;a;a)}\end{array}} \right.\]

Với hình hộp chữ nhật:

 \[\left\{ {\begin{array}{*{20}{c}}{A(0;0;0),B(a;0;0)}\\{C(a;b;0),D(0;b;0)}\\{A'(0;0;b),B'(a;0;b)}\\{C'(a;b;c),D'(0;b;c)}\end{array}} \right.\]

- Cách ghép trục:

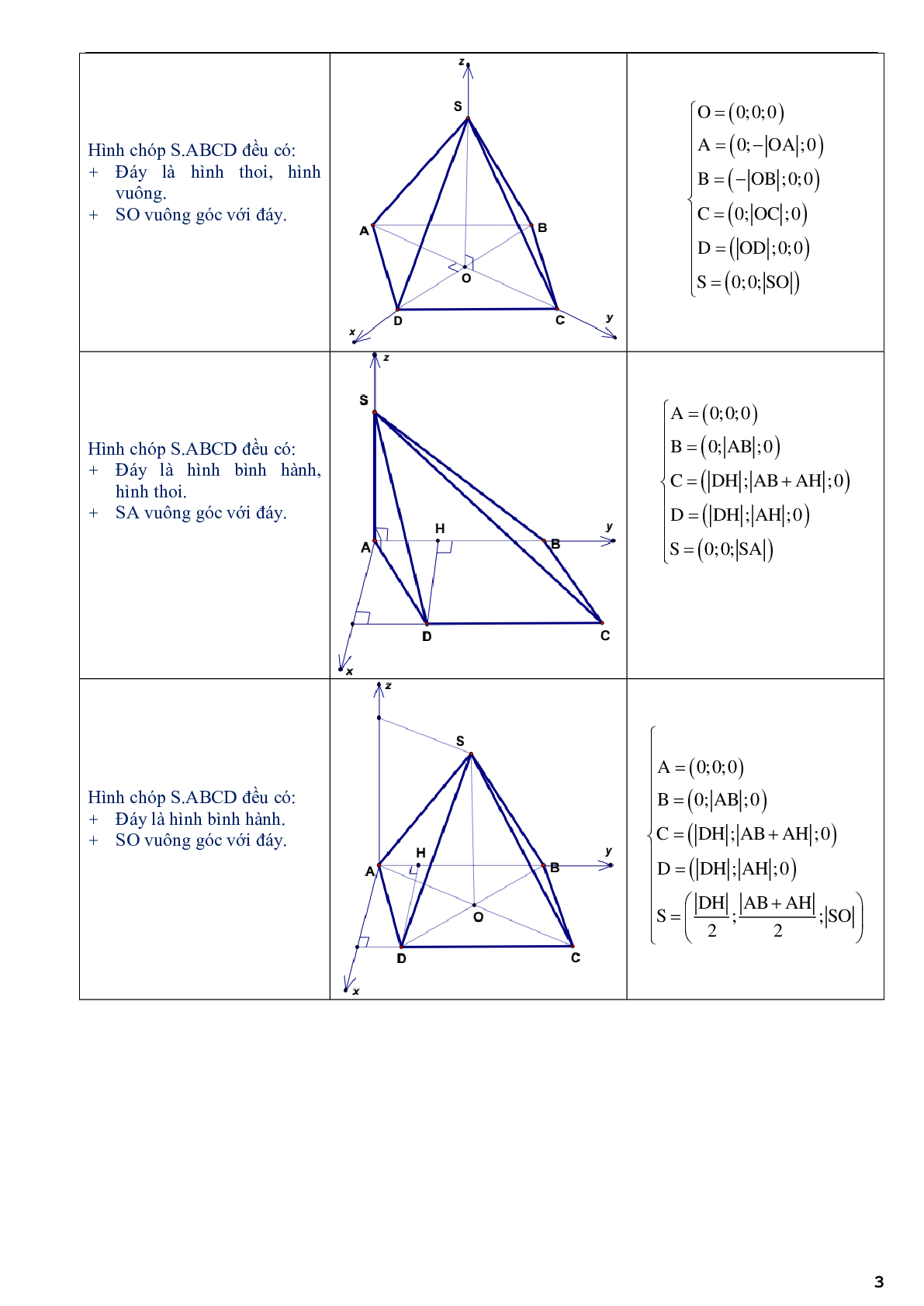
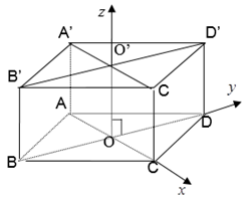
b. Hình hộp ABCD.A¢B¢C¢D¢ có đáy là hình thoi

- Tọa độ các điểm:

Gốc tọa độ trùng với giao điểm O của hai đường chéo của hình thoi ABCD.

Trục Oz đi qua 2 tâm của 2 đáy

- Cách ghép trục:

c. Hình chóp S.ABCD có:

ABCD là hình chữ nhật, hình vuông.

SA ⊥ (ABCD).

- Tọa độ các điểm: \[\left\{ {\begin{array}{*{20}{c}}{A = (0;0;0)}\\{B = \left( {0;|AB|;0} \right)}\\{C = \left( {|AD|;|AB|;0} \right)}\\{D = \left( {|AD|;0;0} \right)}\\{S = \left( {0;0;|SA|} \right)}\end{array}} \right.\]

- Cách ghép trục:

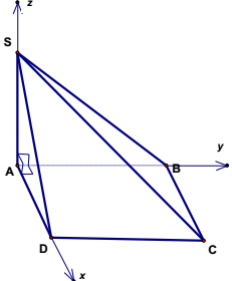
d. Hình chóp S.ABCD có:

Đáy hình chữ nhật, hình vuông.

Các cạnh bên bằng nhau (SO vuông góc với đáy).

- Tọa độ các điểm:

 \[\left\{ {\begin{array}{*{20}{c}}{A = (0;0;0)}\\{B = \left( {0;|AB|;0} \right)}\\{S = \left( {\frac{{|AD|}}{2};\frac{{|AB|}}{s};|SO|} \right)}\\{C = \left( {|AD|;|AB|;0} \right)}\\{D = \left( {|AD|;0;0} \right)}\end{array}} \right.\]

- Cách ghép trục:

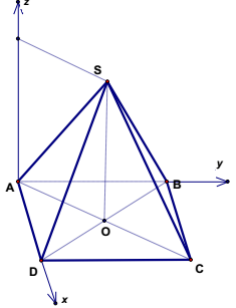
e. Hình chóp S.ABCD đều có:

Đáy là hình thoi, hình vuông.

SO vuông góc với đáy.

- Tọa độ các điểm: \[\left\{ {\begin{array}{*{20}{c}}{O = (0;0;0)}\\{A = (0; - |OA|;0)}\\{B = ( - |OB|;0;0)}\\{C = (0;|OC|;0)}\\{D = (|OD|;0;0)}\\{S = (0;0;|SO|)}\end{array}} \right.\]

- Cách ghép trục:

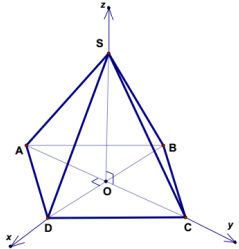
f. Hình chóp S.ABCD đều có:

Đáy là hình bình hành, hình thoi.

SA vuông góc với đáy

- Tọa độ các điểm: \[\left\{ {\begin{array}{*{20}{c}}{A = (0;0;0)}\\{B = \left( {0;|AB|;0} \right)}\\{C = \left( {|DH;|AB + AH|;0} \right)}\\{D = \left( {|DH|;|AH|;0} \right)}\\{S = \left( {0;0;|SA|} \right)}\end{array}} \right.\]

- Cách ghép trục:

g. Hình chóp S.ABCD đều có:

Đáy là hình bình hành.

SO vuông góc với đáy.

- Tọa độ các điểm: \[\left\{ {\begin{array}{*{20}{c}}{A = (0;0;0)}\\{B = \left( {0;|AB|;0} \right)}\\{C = \left( {|DH;|AB + AH|;0} \right)}\\{D = \left( {|DH|;|AH|;0} \right)}\\{S = \left( {\frac{{|DH|}}{2};\frac{{|AB + AH|}}{2};|SO|} \right)}\end{array}} \right.\]

- Cách ghép trục:

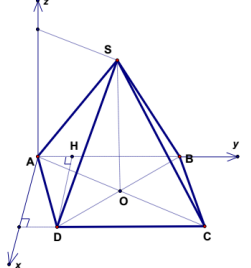
h. Hình chóp S.ABC có:

Đáy là tam giác vuông, tam giác đều.

SA vuông góc với đáy.

- Tọa độ các điểm: \[\left\{ {\begin{array}{*{20}{c}}{A = (0;0;0)}\\{B = \left( {0;|AB|;0} \right)}\\{C = \left( {|CH|;|AH|;0} \right)}\\{S = \left( {0;0;|SA|} \right)}\end{array}} \right.\]

- Cách ghép trục: 

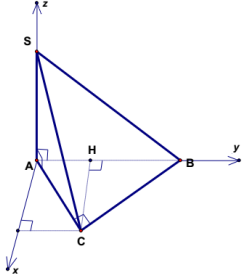
i. Hình chóp S.ABC có:

Đáy là tam giác đều cạnh a.

Các cạnh bên bằng nhau.

- Tọa độ các điểm:

 \[\left\{ {\begin{array}{*{20}{c}}{A = (0;0;0)}\\{B = \left( {0;|AB|;0} \right) = (0;a;0)}\\{C = \left( {|CH|;|AH|;0} \right) = \left( {\frac{{a\sqrt 3 }}{2};\frac{a}{2};0} \right)}\\{S = \left( {|OH|;|AH|;|SO|} \right) = \left( {\frac{{a\sqrt 3 }}{6};\frac{a}{2};|SO|} \right)}\end{array}} \right.\]

- Cách ghép trục:

Trên đây là một số dạng cơ bản của một số loại hình khối mà chúng ta có thể tọa độ hóa một cách đơn giản. Các em lưu ý rằng chúng ta có thể tọa độ hóa một khối đa diện bất kỳ. Chỉ cần chúng ta xác định được đường cao của khối đa diện đó và thông thường trên lý thuyết ta đều đặt gốc tọa độ là chân đường cao của khối đa diện; trục cao (trục Oz) là đường cao, sau đó ta dựng hai tia còn lại. Nhưng trong thực hành giải toán chúng ta căn cứ tùy bài toán để đặt hệ trục miễn sao chúng ta có thể tìm các tọa độ các đỉnh liên quan đến hình khối cần tính có thể tìm được một cách dễ dàng hoặc không quá phức tạp.

Ví dụ như bài toán sau: (Các em hãy xem và suy nghĩ nên đặt hệ trục ra sao).

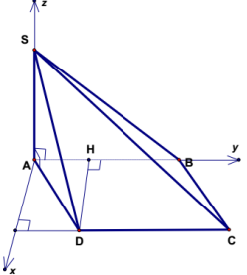
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, mặt phẳng (SBC) tạo với đáy góc 60⁰ . Mặt bên (SAB) vuông góc với đáy, tam giác SAB cân tại S. Tính thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng SA, BC.

Bình luận: Rõ ràng rằng việc tính thể tích của khối chóp này là không quá khó khăn, chỉ cần các em nắm được cách xác định góc giữa hai mặt phẳng là xác định được. Vì vậy, ý tính thể tích thầy để các em tự suy nghĩ và thực hiện.

Với câu hỏi tính khoảng cách giữa hai đường thẳng chéo nhau này, các em hoàn toàn có thể thực hiện theo hình tổng hợp. Ở đây chúng ta bàn luận về việc đặt hệ trục tọa độ để thực hiện ý thứ hai này.

Trước hết các em cần lưu ý: Xác định chiều cao của hình chóp này như thế nào?

Điều này là không quá khó: Vì sao? Hãy nhớ: “Nếu hai mặt phẳng vuông góc với nhau, trong mặt này dựng một đường thẳng vuông góc với giao tuyến thì đường thẳng đó vuông góc với mặt phẳng kia”. Gắn vào hình chóp này: Ta thấy mặt phẳng (SAB) vuông góc với mặt đáy, mà giao tuyến của hai mặt phẳng này là AB. Ta cần tìm chiều cao cho nên, các em chỉ cần từ S dựng SH vuông góc với AB, (H Î AB) vì tam giác SAB cân tại S cho nên H là trung điểm AB. Tức là các em đã xác định được chiều cao và chân đường vuông góc.

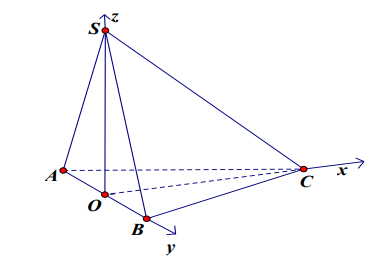
Vậy chúng ta có thể đặt hệ trục tọa độ rồi. Các em vẽ hình và đặt hệ trục như sau:

Tính toán tọa độ các điểm (căn cứ vào phần trước),

ta có: \[\left\{ {\begin{array}{*{20}{c}}{O(0;0;0),S\left( {0;0;\frac{{3a}}{4}} \right)}\\{A\left( {0; - \frac{a}{2};0} \right),B\left( {0;\frac{a}{2};0} \right),C(a;0;0)}\end{array}} \right.\]

Áp dụng công thức tính khoảng cách giữa hai đường thẳng chéo nhau: SA, BC ta có:

\[d\left( {SA,BC} \right) = \frac{{\left| {\left[ {\overrightarrow {SA} ,\overrightarrow {BC} } \right].\overrightarrow {AB} } \right|}}{{\left| {\left[ {\overrightarrow {SA} ,\overrightarrow {BC} } \right]} \right|}}\], ta thu được kết quả cần tính.

Kể ra thì cũng không quá phức tạp đúng không các em. Các em hãy suy nghĩ có cách đặt hệ trục tọa độ nào khác không? Ở mục số 4. Ví dụ minh họa, thầy sẽ trình bày thêm một số ví dụ cụ thể về các dạng toán để các em hiểu rõ hơn về phương pháp này.

3. Sử dụng các kiến thức về tọa độ để giải quyết bài toán

a) Khoảng cách giữa 2 điểm

Khoảng cách giữa hai điểm A(x_A;y_A;z_A) và B(x_B;y_B;z_B) là:

\[AB = \sqrt {{{({x_B} - {x_A})}^2} + \sqrt {{{({y_B} - {y_A})}^2} + } \sqrt {{{({z_B} - {z_A})}^2}} } \]

b) Khoảng cách từ điểm đến đoạn thẳng

Tính khoảng cách từ A đến đường thẳng D ?

Cách 1: Cho đường thẳng D đi qua M, có một vectơ chỉ phương \[\overrightarrow u \]và một điểm A. Khoảng cách từ A đến đường thẳng D được tính bởi công thức:

\[d\left( {A,\Delta } \right) = \frac{{\left| {\left[ {\overrightarrow u ,\overrightarrow {AM} } \right]} \right|}}{{\left| {\overrightarrow u } \right|}}\]

Cách 2:

Lập phương trình mặt phẳng (a) đi qua A và vuông góc với D .

Tìm tọa độ giao điểm H của (a) và D .

d(M, d) = MH.

c) Khoảng cách từ điểm đến mặt phẳng

Khoảng cách từ M (x₀;y₀;z₀) đến mặt phẳng (P) \[Ax + By + Cz + D = 0\] là:

\[d({M_0},(P)) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\]

d) Khoảng cách giữa hai mặt phẳng song song

Định nghĩa: Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia.