Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Phương pháp tọa độ hóa để giải bài toán hình học không gian, tài liệu bao gồm 16 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Phương pháp tọa độ hóa để giải bài toán hình học không gian

I. Các công thức

1. Véc tơ trong không gian

Trong không gian cho các véc tơ \[\overrightarrow {{u_1}}  = ({x_1},{y_1},{z_1}),\overrightarrow {{u_2}}  = ({x_2},{y_2},{z_2})\]và số k tùy ý

\[\overrightarrow {{u_1}}  = \overrightarrow {{u_2}}  \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_1} = {x_2}}\\{{y_1} = {y_2}}\\{{z_1} = {z_2}}\end{array}} \right.\]

\[\overrightarrow {{u_1}}  \pm \overrightarrow {{u_2}}  = ({x_1} \pm {x_2};{y_1} \pm {y_2};{z_1} \pm {z_2})\]

\[k\overrightarrow {{u_1}}  = (k{x_1};k{y_1};k{z_1})\]

Tích có hướng: \[\overrightarrow {{u_1}} .\overrightarrow {{u_2}}  = {x_1}.{x_2} + {y_1}.{y_2} + {z_1}.{z_2}\]

Hai véc tơ vuông góc nhau

\[ \Leftrightarrow \overrightarrow {{u_1}} .\overrightarrow {{u_2}}  = 0 \Leftrightarrow {x_1}.{x_2} + {y_1}.{y_2} + {z_1}.{z_2} = 0\]

\[\left| {\overrightarrow {{u_1}} } \right| = \sqrt {x_1^2 + y_1^2 + z_1^2} \]

Gọi \[\varphi \] là góc hợp bởi hai véc tơ \[({0^0} \le \varphi  \le {180^0})\]

\[\begin{array}{l}\cos \varphi  = \cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = \frac{{\overrightarrow {{u_1}} .\overrightarrow {{u_2}} }}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}}\\ = \frac{{{x_1}.{x_2} + {y_1}.{y_2} + {z_1}.{z_2}}}{{\sqrt {x_1^2 + y_1^2 + z_1^2} .\sqrt {x_2^2 + y_2^2 + z_2^2} }}\end{array}\]

\[\overrightarrow {AB}  = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\].

\[AB = \sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2} + {{({z_B} - {z_A})}^2}} \]

Tọa độ các điểm đặc biệt:

Tọa độ trung điểm I của đoạn thẳng AB là

\[I = (\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\]

Tọa độ trọng tâm G của tam giác ABC là

\[G = (\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\]

Tọa độ trọng tâm G của tứ diện ABCD là

\[G = (\frac{{{x_A} + {x_B} + {x_C} + {x_D}}}{4};\frac{{{y_A} + {y_B} + {y_C} + {y_D}}}{4};\frac{{{z_A} + {z_B} + {z_C} + {z_D}}}{4})\]

Tích có hướng của hai vectơ là 1 vectơ vuông góc cả hai vectơ xác định bởi

\[\overrightarrow u  = \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}{{y_1}}&{{z_1}}\\{{y_2}}&{{z_2}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{{z_1}}&{{x_1}}\\{{z_2}}&{{x_2}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{{x_1}}&{{z_1}}\\{{x_2}}&{{z_2}}\end{array}} \right|} \right)\]

Một số tính chất của tích có hướng:

\[\overrightarrow a \]cùng phương với \[\overrightarrow b \]\[ \Leftrightarrow \left[ {\overrightarrow a ,\overrightarrow b } \right] = \overrightarrow 0 \].

A, B, C thẳng hàng \[ \Leftrightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \overrightarrow 0 \]

Ba vec tơ \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \]đồng phẳng \[ \Leftrightarrow \left[ {\overrightarrow a ,\overrightarrow b } \right].\overrightarrow c  = 0\].

Bốn điểm A, B, C, D không đồng phẳng \[ \Leftrightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD}  \ne \overrightarrow 0 \].

\[\left| {\left[ {\overrightarrow a ,\overrightarrow b } \right]} \right| = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\sin (\overrightarrow a ,\overrightarrow b )\]

Các ứng dụng của tích có hướng

Diện tích hình bình hành: \[{S_{ABCD}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right]} \right|\].

Diện tích tam giác: \[{S_{\Delta ABC}} = \frac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right|\].

Thể tích hình hộp: \[{V_{ABCD.A'B'C'D'}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AA'} } \right|\]

Thể tích tứ diện: \[{V_{ABCD}} = \frac{1}{6}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} } \right|\]

2. Phương trình mặt phẳng

Phương trình tổng quát \[(\alpha ):ax + by + cz + d = 0\] với \[{a^2} + {b^2} + {c^2} \ne 0\].

Phương trình mặt phẳng\[(\alpha )\] qua M (x₀;y₀;z₀) và có véc tơ pháp tuyến \[\overrightarrow n  = (a;b;c)\]

\[(\alpha ):a(x - {x_0}) + b(y - {y_0}) + c(z - {z_0}) = 0\]

Phương trình mặt phẳng theo đoạn chắn: (α) qua A(a, 0, 0);B(0,b, 0);C (0, 0, c)

\[(\alpha ):\frac{{x - {x_0}}}{a} + \frac{{y - {y_0}}}{b} + \frac{{z - {z_0}}}{c} = 1\] với a, b, c ≠ 0

• Nếu \[\overrightarrow n  = (a;b;c)\]là vectơ pháp tuyến của (α) thì \[k\overrightarrow n \], k ≠ 0 cũng là vectơ pháp tuyến của (α). Do đó một mặt phẳng có vô số vectơ pháp tuyến. Trong một số trường hợp ta có thể tìm vectơ pháp tuyến bằng cách chọn một giá trị cụ thể cho a (hoặc b hoặc c) và tính hai giá trị còn lại đảm bảo đúng tỉ lệ a : b : c .

3. Góc

Góc giữa hai mặt phẳng: Cho mặt phẳng (α) có vectơ pháp tuyến là \[\overrightarrow {{n_\alpha }} \], mặt phẳng

(\[\beta \]) có véc tơ pháp tuyến là \[\overrightarrow {{n_\beta }} \], khi đó góc giữa \[(\alpha )\]và \[(\beta )\]được tính bằng

\[\cos \left( {(\alpha )(\beta )} \right) = \left| {cos\left( {\overrightarrow {{n_\alpha }} ,\overrightarrow {{n_\beta }} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_\alpha }} .\overrightarrow {{n_\beta }} } \right|}}{{\left| {\overrightarrow {{n_\alpha }} } \right|.\left| {\overrightarrow {{n_\beta }} } \right|}}\]

Góc giữa hai đường thẳng: Cho hai đường thẳng d₁ và d₂ có các vectơ chỉ phương là \[\overrightarrow {{u_1}} \] và \[\overrightarrow {{u_2}} \], khi đó góc giữa d₁ và d₂ tính bằng

\[\cos \left( {{d_1},{d_2}} \right) = \left| {cos\left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}}\]

Góc giữa đường thẳng và mặt phẳng: Cho đường thẳng d có vectơ chỉ phương \[\overrightarrow u \], mặt phẳng (α) có vectơ pháp tuyến là \[\overrightarrow n \], khi đó góc giữa d và (α) là ϕ được tính bằng

\[\sin \varphi  = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}}\]

4. Khoảng cách

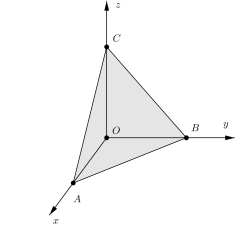
Khoảng cách từ điểm A (x₀;y₀;z₀) tới \[(\alpha ):ax + by + cz + d = 0\]là

\[d\left( {A,(\alpha )} \right) = \frac{{\left| {ax + by + cz + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\]

Khoảng cách từ điểm M tới đường thẳng ∆ qua M₀ và có vectơ chỉ phương \[\overrightarrow u \] là

\[d\left( {A,\Delta } \right) = \frac{{\left| {\left[ {\overrightarrow {M{M_0}} ,\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}}\]

Khoảng cách giữa hai đường thẳng chéo nhau ∆₁ và ∆₂ biết ∆₁ qua M₁ và có vectơ chỉ phương \[\overrightarrow {{u_1}} \]; ∆₂ qua M₂ và có vectơ chỉ phương \[\overrightarrow {{u_2}} \]

\[d\left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}} } \right|}}{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right]} \right|}}\]

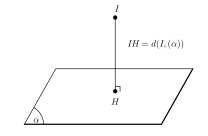
Khoảng cách giữa hai mặt phẳng (α) và \[(\beta )\]song song nhau là khoảng cách từ M₀ \[ \in \](α) tới \[(\beta )\].

Khoảng cách giữa hai đường phẳng ∆₁ và ∆₂ song song nhau là khoảng cách từ M₁ \[ \in \]∆₁ tới ∆₂.

Khoảng cách giữa hai đường thẳng d và mặt phẳng (α) song song nhau là khoảng cách từ M₀ \[ \in \] d tới (α).

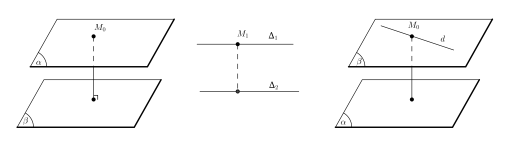
II. Xác định tọa độ điểm

1. Tọa độ điểm trên trục tọa độ

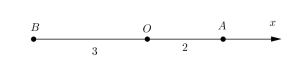
Tìm tọa độ điểm A trên trục tọa độ ta tìm khoảng cách từ A đến gốc tọa độ và dựa vào chiều dương đã chọn để xác định tọa độ A.

Ví dụ chọn tia OA trùng tia Ox, điểm A và B nằm trên Ox

OA = 2 ⇒ A (0,0,2).

OB = 3 ⇒ B (0,0,−3) (do B nằm ở phần âm)

2. Tọa độ điểm trên mặt phẳng tọa độ

Tìm tọa độ của A trên 1 mặt phẳng tọa độ ta tìm hình chiếu của A trên các trục tọa độ và dựa vào các tọa độ hình chiếu này để xác định tọa độ A.

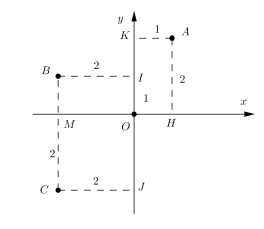
Ví dụ các điểm A,B,C có hình chiếu trên các trục với độ dài như hình vẽ, theo chiều dương đã chọn ta được

AK = 1 = x_K, AH = 2 = y_K : tọa độ A(1, 2)

BI = 2 = −x_B (do B nằm phần âm của trục hoành),BM = 1 = y_B : tọa độ B(−2, 1)

CJ = 2, CM = 2: tọa độ C (−2,−2) (do C nằm ở phần âm của trục tung và trục hoành)

3. Tọa độ điểm trường hợp tổng quát

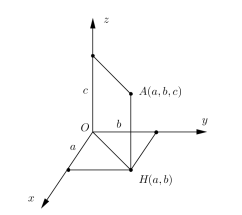
Tìm tọa độ của A đầu tiên ta tìm tọa độ hình chiếu H của A lên mặt phẳng tọa độ bất kì, sau đó ta tính độ dài AH . Tọa độ A xác định nhờ tọa độ H và độ dài AH.

Ví dụ: tọa độ hình chiếu vuông góc của A lên mặt phẳng Oxy là H (a,b), ta tính được AH = c thì khi đó A có tọa độ A(a,b,c) (giả sử rằng các thành phần tọa độ A đều nằm trong phần dương).

III. Cách chọn hệ trục tọa độ - chọn véctơ

1. Chọn véctơ

Đối với dạng bài tập này khi tìm véctơ chỉ phương, véctơ pháp tuyến của đường thẳng và mặt phẳng ta sẽ gặp trường hợp véctơ chứa tham số a là độ dài cạnh. Khi đó, để tiện cho việc tính toán ta chọn lại véctơ chỉ phương, véctơ pháp tuyến mất tham số a.

Ví dụ: véctơ chỉ phương của mặt phẳng (α) là \[\overrightarrow {SA}  = \left( {a, - 3a,\frac{a}{3}} \right)\] thì ta có thể chọn lại véctơ chỉ phương khác là \[\overrightarrow u  = \left( {1, - 3,\frac{a}{3}} \right)\].

Trường hợp khoảng cách từ 1 điểm đến 1 đường thẳng, khoảng cách giữa 2 đường thẳng chéo nhau thì véctơ \[\overrightarrow {{M_1}{M_2}} \] ta giữ nguyên.

2. Chọn hệ trục tọa độ

Phần quan trọng nhất của phương pháp này là cách chọn hệ trục tọa độ. Không có phương pháp tổng quát, có nhiều hệ trục tọa độ có thể được chọn, chúng ta chọn sao cho việc tìm tọa độ các điểm có nhiều số 0 càng tốt.

Hệ trục tọa độ nằm trên 3 đường thẳng đôi 1 vuông góc nhau.

Gốc tọa độ thường là chân đường cao của hình chóp, hình lăng trụ trùng với đỉnh của hình vuông, hình chữ nhật, tam giác vuông hoặc có thể là trung điểm của cạnh nào đó,...