Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Hướng dẫn giải một số bài tập tọa độ trong không gian nâng cao, tài liệu bao gồm 22 trang, 35 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Hướng dẫn giải một số bài tập tọa độ trong không gian nâng cao

Câu 1. Tìm m để góc giữa hai vectơ: \[\overrightarrow u  = (1;{\log _3}5;{\log _m}2)\], \[\overrightarrow v  = (3;{\log _3}3;4)\]là góc nhọn. Chọn phương án đúng và đầy đủ nhất.

A. \[m > \frac{1}{2},m \ne 1\]

B. \[m > 1\]hoặc \[0 < m < \frac{1}{2}\]

C. \[0 < m < \frac{1}{2}\]

D. \[m > 1\]

Giải

Ta có \[\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{\overrightarrow u .\overrightarrow v }}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}} = \frac{{3 + {{\log }_3}5.{{\log }_5}3 + 4{{\log }_m}2}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}}\]. Do mẫu số luôn lớn hơn 0 nên ta đi tìm điều kiện để tử số dương.

Mặt khác

\[\begin{array}{l}3 + {\log _3}5.{\log _5}3 + 4{\log _m}2 > 0\\ \Leftrightarrow 4{\log _m}2 >  - 4\\ \Leftrightarrow {\log _m}2 >  - 1 \Leftrightarrow {\log _m}2 > {\log _m}\frac{1}{m}\end{array}\]

Với 0 < m < 1 thì \[ \Leftrightarrow \frac{1}{m} > 2 \Leftrightarrow m > \frac{1}{2}\]. Kết hợp điều kiện suy ra m > 1.

Vậy \[m > 1\]hoặc \[0 < m < \frac{1}{2}\]

Câu 2. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):\[3x - 3y + 2z + 37 = 0\]các điểm A (4;1;5), B(3;0;1), C(-1;2;0). Điểm M(a;b;c) thuộc (P) sao cho biểu thức \[P = \overrightarrow {MA} .\overrightarrow {MB}  + \overrightarrow {MB} .\overrightarrow {MC}  + \overrightarrow {MC} .\overrightarrow {MA} \]đạt giá trị nhỏ nhất, khi đó \[a + b + c\]bằng:

A. 10

B. 13

C. 9

D. 1

Giải

\[M(a;b;c) \Rightarrow P = 3\left[ {{{(a - 2)}^2} + {{(b - 1)}^2} + {{(c - 2)}^2} - 5} \right]\]

\[\begin{array}{l}M \in P \Rightarrow 3a - 3b + 2c + 37 = 0\\ \Leftrightarrow 3(a - 2) - 3(b - 1) + 2(c - 2) =  - 44\end{array}\]

Áp dụng BĐT Bunhiacốpxki ta có:

\[ - 44 = {\left[ {3(a - 2) - 3(b - 1) + 2(c - 2)} \right]^2} \le ({3^2} + {3^2} + {2^2})\left[ {{{(a - 2)}^2} + {{(b - 1)}^2} + {{(c - 2)}^2}} \right]\]

\[ \Rightarrow {(a - 2)^2} + {(b - 1)^2} + {(c - 2)^2} \ge \frac{{{{( - 44)}^2}}}{{{3^2} + {3^2} + {2^2}}} = 88\]

Dấu “=” xảy ra khi và chỉ khi:

\[\begin{array}{l}\frac{{a - 2}}{3} = \frac{{b - 1}}{{ - 3}} = \frac{{c - 2}}{2}\\ \Leftrightarrow M( - 4;7; - 2) \Rightarrow a + b + c = 1\end{array}\]

Câu 3. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): \[2x - y + 2 = 0\]và đường thẳng d_m: \[\left\{ {\begin{array}{*{20}{c}}{(2m + 1)x + (1 - m)y + m - 1 = 0}\\{mx + (2m - 1)z + 4m + 2 = 0}\end{array}} \right.\] (m là tham số). Tìm m để đường thẳng d_m song song với mặt phẳng (P).

A. \[m = \frac{1}{2}\]

B. \[m = 1\]

C. \[m =  - \frac{1}{2}\]

D. \[m =  - 1\]

Giải

(d_m) // (P) \[ \Leftrightarrow \]hệ PT ẩn x, y, z sau vô nghiệm:

\[\left\{ {\begin{array}{*{20}{c}}{2x - y + 2 = 0}\\\begin{array}{l}(2m + 1)x + (1 - m)y + m - 1 = 0\\mx + (2m - 1)z + 4m + 2 = 0\end{array}\end{array}} \right.\]

(1) \[ \Rightarrow y = 2x + 2\]. Thay vào (2) ta được

\[x = \frac{{m - 1}}{3} \Rightarrow y = \frac{{2m + 4}}{3}\]

Thay x, y vào (3) ta được:

 \[(2m + 1)z =  - \frac{1}{3}({m^2} + 11m + 6)\].

Để PT này vô nghiệm thì \[m =  - \frac{1}{2}\].

Câu 4. Trong không gian với hệ tọa độ Oxyz, một mặt phẳng đi qua điểm M (1;3;9) và cắt các tia Ox, Oy, Oz lần lượt tại A (a;0;0), B (0;b;0), C (0;0;c) với a, b, c là các số thực dương. Tìm giá trị của biểu thức P = a + b + c để thể tích tứ diện OABC đạt giá trị nhỏ nhất.

A. P = 44

B. P = 39

C. P = 27

D. P = 16

Giải

\[{V_{OABC}} = \frac{1}{6}OA.OB.OC = \frac{1}{6}abc\]

Phương trình mặt phẳng đi qua A, B, C: \[\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\]

Vì \[M \in (ABC) \Rightarrow \frac{1}{a} + \frac{3}{b} + \frac{9}{c} = 1\]

Áp dụng BĐT Côsi :

\[\begin{array}{l}1 = \frac{1}{a} + \frac{3}{b} + \frac{9}{c} \ge 3\sqrt[3]{{\frac{1}{a}.\frac{3}{b}.\frac{9}{c}}} \Rightarrow 1 \ge \frac{{27.27}}{{abc}}\\ \Rightarrow \frac{1}{6}abc \ge 121,5 = \min {V_{OABC}}\end{array}\]

Dấu “=” xảy ra khi và chỉ khi:

\[\left\{ {\begin{array}{*{20}{c}}{\frac{1}{a} + \frac{3}{b} + \frac{9}{c} = 1}\\{\frac{1}{a} = \frac{3}{b} = \frac{9}{c}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 3}\\{b = 9}\\{c = 27}\end{array}} \right.\]

\[ \Rightarrow a + b + c = 39\]

Câu 5. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \[\Delta :\frac{{x - 1}}{1} = \frac{y}{2} = \frac{{z + 1}}{{ - 1}}\]và ba điểm A(3;2;-1), B(-3;-2;3), C(5;4;-7). Gọi tọa độ điểm M(a;b;c) nằm trên \[\Delta \]sao cho MA + MB nhỏ nhất, khi đó giá trị của biểu thức P = a + b + c là:

A. \[P = \frac{{16 + 6\sqrt 6 }}{5}\]

B. \[P = \frac{{42 - 6\sqrt 6 }}{5}\]

C. \[P = \frac{{16 - 6\sqrt 6 }}{5}\]

D. \[P = \frac{{16 + 12\sqrt 6 }}{5}\]

Giải

\[M \in \Delta \]nên \[M(1 + t;2t; - 1 - t)\]

\[\overrightarrow {AM}  = (t - 2;2t - 2; - t)\]\[ \Rightarrow AM = \sqrt {6{t^2} - 12t + 8} \]

\[\overrightarrow {BM}  = (t + 4;2t + 2; - t - 4)\]\[ \Rightarrow BM = \sqrt {6{t^2} + 24t + 36} \]

\[\begin{array}{l}MA + MB = \sqrt {6{t^2} - 12t + 8}  + \sqrt {6{t^2} + 24t + 36} \\ = \sqrt 6 \left[ {\underbrace {\sqrt {{{(1 - t)}^2} + \frac{1}{3}}  + \sqrt {{{(t + 2)}^2} + 2} }_{f(x)}} \right]\end{array}\]

Áp dụng BĐT Vec tơ ta có: 

\[\begin{array}{l}f(x) \ge \sqrt {{{\left( {1 - t + t + 2} \right)}^2} + {{\left( {\frac{1}{{\sqrt 3 }} + \sqrt 2 } \right)}^2}} \\ = \sqrt {9 + {{\left( {\frac{1}{{\sqrt 3 }} + \sqrt 2 } \right)}^2}} \end{array}\]

Dấu “=” xảy ra khi và chỉ khi:

\[\frac{{1 - t}}{{\frac{1}{{\sqrt 3 }}}} = \frac{{t + 2}}{{\sqrt 2 }} \Rightarrow t = \frac{{8 - 3\sqrt 6 }}{5}\]

Do đó:

\[\begin{array}{l}M\left( {\frac{{13 - 3\sqrt 6 }}{5};\frac{{16 - 6\sqrt 6 }}{5};\frac{{3\sqrt 6  - 13}}{5}} \right)\\ \Rightarrow P = \frac{{16 - 6\sqrt 6 }}{5}\end{array}\]

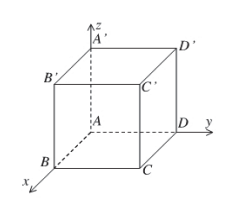
Câu 6. Trong không gian với hệ tọa độ Oxyz, cho hình chữ nhật ABCD.A’B’C’D’ có A trùng với gốc tọa độ. Cho B(a;0;0), D(0;a;0), A’(0;0;b) với a, b > 0. Gọi M là trung điểm của cạnh CC’. Xác định tỉ số \[\frac{a}{b}\]để hai mặt phẳng (A’BD) và (BDM) vuông góc với nhau.

A. \[\frac{a}{b} = 2\]

B. \[\frac{a}{b} = \frac{1}{2}\]

C. \[\frac{a}{b} = 3\]

D. \[\frac{a}{b} = 1\]

Từ giả thiết ta có: C(a;a;0); C(a;a;b) \[ \Rightarrow M\left( {a;a;\frac{b}{2}} \right)\]

Mặt phẳng (BDM) có VTPT là:

Mặt phẳng (A’BD) có VTPT là:

Yêu cầu của bài toán tương đương với:

\[\begin{array}{l}\overrightarrow {{n_1}} .\overrightarrow {{n_2}}  = 0 \Leftrightarrow \frac{{{a^2}{b^2}}}{2} + \frac{{{a^2}{b^2}}}{2} - {a^4} = 0\\ \Leftrightarrow a = b \Leftrightarrow \frac{a}{b} = 1\end{array}\]

Câu 7. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \[\Delta :\frac{{x - 1}}{2} = \frac{y}{1} = \frac{{z + 1}}{{ - 1}}\]và mặt phẳng (P): 2x – y + 2z – 1 = 0. Mặt phẳng (Q) chứa \[\Delta \]và tạo với (P) một góc \[\alpha \]nhỏ nhất, khi đó góc \[\alpha \]gần với giá trị nào nhất sau đây?

A. 6⁰

B. 8⁰

C. 10⁰

D. 5⁰

Giải

\[\Delta :\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\\begin{array}{l}y = t\\z =  - 1 - t\end{array}\end{array}} \right.\]. Chọn 2 điểm (1;0;-1) và (3;1;-2) với t = 1.

(Q) chứa \[\Delta \]suy ra (Q): \[a(x - 1) + by + c(z + 1) = 0 \Rightarrow ax + by + cz - a + c = 0\]

Và (3;1;-2) \[ \in \](Q) \[ \Rightarrow 3a + b - 2c - a + c = 0 \Rightarrow 2a + b - c = 0 \Rightarrow c = 2a + b\]

Vậy (Q): \[ax + by + (2a + b)z + a + b = 0\]. Gọi \[\alpha  = \left( {(P),(Q)} \right),\alpha  \in \left[ {{0^0};{{90}^0}} \right]\]

Ta có: \[\cos \alpha  = \frac{{\left| {\overrightarrow {{n_P}} .\overrightarrow {{n_Q}} } \right|}}{{\left| {\overrightarrow {{n_P}} } \right|\left| {\overrightarrow {{n_Q}} } \right|}} = \frac{{\left| {b + 6a} \right|}}{{3\sqrt {{a^2} + {b^2} + {{(2a + b)}^2}} }} = \frac{1}{3}\sqrt {\frac{{{b^2} + 12ab + 36{a^2}}}{{2{b^2} + 4ab + 5{a^2}}}} \]

Nếu \[a = 0 \Rightarrow \cos \alpha  = \frac{1}{{3\sqrt 2 }}\]

Nếu \[a \ne 0\], đặt \[t = \frac{b}{a}\]thì ta có: \[\frac{{{b^2} + 12ab + 36{a^2}}}{{2{b^2} + 4ab + 5{a^2}}} = \frac{{{t^2} + 12t + 36}}{{2{t^2} + 4t + 5}} = f(t)\]

\[f'(t) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t =  - \frac{7}{{10}}}\\{t =  - 6}\end{array}} \right.\]. Từ bảng biến thiên ta có thể dễ nhận thấy:

\[\max f(t) = f\left( { - \frac{7}{{10}}} \right) = \frac{{53}}{6} \Rightarrow \alpha  = {\cos ^{ - 1}}\left( {\frac{1}{3}\sqrt {\frac{{53}}{6}} } \right) \approx {8^0}\]

Câu 8. Trong không gian với hệ tọa độ Oxyz, cho điểm A (0;1;1), B (1;0;-3), C (-1;-2;-3) và mặt cầu (S): \[{x^2} + {y^2} + {z^2} - 2x + 2z - 2 = 0\]. Điểm D (a;b;c) trên mặt cầu (S) sao cho tứ diện ABCD có thể tích lớn nhất, khi đó a + b + c bằng:

A. \[ - \frac{2}{3}\]

B. \[\frac{2}{3}\]

C. 1

D. \[\frac{4}{3}\]

Giải

Tâm I(1;0;-1), bán kính R = 2. (ABC): \[2x + 2y + z + 1 = 0\]

\[{V_{ABCD}} = \frac{1}{3}d\left( {D;(ABD)} \right).{S_{ABC}}\]khi đó \[{V_{ABCD}}\]max khi và chỉ khi \[d\left( {D;(ABD)} \right)\]max.

Gọi D₁D₂ là đường kính của (S) vuông góc với (ABC). Ta thấy với D là điểm bất kì thuộc (S) thì \[d\left( {D;(ABD)} \right) \le \max \left\{ {d\left( {{D_1};(ABC)} \right),d\left( {{D_2};(ABC)} \right)} \right\}\]

Dấu”=” xảy ra khi D trùng với D₁ hoặc D₂.

\[{D_1}{D_2}:\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\\begin{array}{l}y =  - 2t\\z =  - 1 + t\end{array}\end{array}} \right.\]thay vào (S) ta suy ra: \[\left[ {\begin{array}{*{20}{c}}{t = \frac{2}{3}}\\{t =  - \frac{2}{3}}\end{array}} \right. \Rightarrow {D_1}\left( {\frac{7}{3}; - \frac{4}{3}; - \frac{1}{3}} \right),{D_2}\left( { - \frac{1}{3};\frac{4}{3}; - \frac{5}{3}} \right)\]

Vì \[d\left( {{D_1};(ABC)} \right) > d\left( {{D_2};(ABC)} \right)\]nên \[D\left( {\frac{7}{3}; - \frac{4}{3}; - \frac{1}{3}} \right)\] \[ \Rightarrow a + b + c = \frac{2}{3}\]

Câu 9. Cho mặt cầu (S): \[{x^2} + {y^2} + {z^2} - 2x + 4z + 1 = 0\] và đường thẳng d: \[\left\{ {\begin{array}{*{20}{c}}{x = 2 - t}\\\begin{array}{l}y = t\\z = m + t\end{array}\end{array}} \right.\]. Tìm m để d cắt (S) tại hai điểm phân biệt A, B sao cho các mặt phẳng tiếp diện của (S) tại A và B vuông góc với nhau.

A. m = -1 hoặc m = -4

B. m = 0 hoặc m = -4

C. m = -1 hoặc m = 0

D. Cả A, B, C đều sai

Giải

Bình luận: Ta có nếu hai mặt phẳng tiếp diện của (S) tại A và B vuông góc với nhau thì hai vtpt của hai mặt phẳng này cũng vuông góc với nhau. Mà hai vtpt của hai mặt phẳng này chính là \[\overrightarrow {IA} ,\overrightarrow {IB} \]. Với I(1;0;-2) là tâm của mặt cầu (S).