Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề hiểu rõ bản chất hình học của bài toán cực trị tọa độ không gian, tài liệu bao gồm 12 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề hiểu rõ bản chất hình học của bài toán cực trị tọa độ không gian, tài liệu bao gồm 12 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Chuyên đề hiểu rõ bản chất hình học của bài toán cực trị tọa độ không gian

Hiểu rõ bản chất hình học của bài toán cực trị tọa độ không gian để giải nhanh bài toán trắc nghiệm.

Để giải nhanh bài toán cực trị trong hình học tọa độ không gian, chúng ta cần tìm được vị trí đặc biệt của nghiệm hình để cực trị ( số đo góc, khoảng cách, độ dài ) xảy ra. Khi biết vị trí đặc biệt đó, việc tính toán chỉ còn vài dòng đơn giản là ra kết quả. Sau đây các các bài toán cực trị thường gặp, bản chất hình học của nó và công thức giải nhanh bài toán đó.

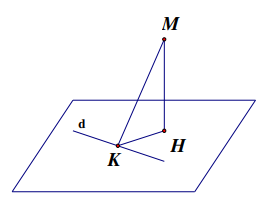
Bài toán 1: Viết phương trình mặt phẳng đi qua một đường thẳng d và cách một điểm M ∉ d một khoảng lớn nhất.

Giải: Gọi hình chiếu vuông góc của M trên mặt phẳng và d lần lượt là H, K. Ta có khoảng cách từ M đến mặt phẳng là đoạn MH ≤ MK. Vậy MH lớn nhất khi và chỉ khi H trùng K. Hay mặt phẳng chứa d và vuông góc với mặt phẳng chứa M và d.

Mặt phẳng cần tìm có véctơ pháp tuyến \[\overrightarrow n  = \left[ {\left[ {\overrightarrow {{u_d}} ;\overrightarrow {AM} } \right],\overrightarrow {{u_d}} } \right]\]trong đó A ∈ d.

Ví dụ 1: Viết phương trình mp chứa đường thẳng d: \[\frac{{x - 1}}{2} = \frac{y}{1} = \frac{{z + 2}}{{ - 1}}\] và cách M (2;1;1) một khoảng lớn nhất.

Giải:

Ta có \[\overrightarrow {{u_d}}  = (2;1; - 1),A = (1;0; - 2) \Rightarrow \overrightarrow {AM}  = (1;1;3)\]

Vậy \[\overrightarrow n  = \left[ {\left[ {\overrightarrow {{u_d}} ;\overrightarrow {AM} } \right],\overrightarrow {{u_d}} } \right] = ( - 6; - 6; - 18)\].

Vậy phương trình mặt phẳng cần tìm là:

 \[(x - 1) + y + 3(z + 2) = 0 \Leftrightarrow x + y + 3z + 5 = 0\].

Ví dụ 2: Viết phương trình mp đi qua điểm A(1;− 2;1), song song với đường thẳng d: \[\frac{x}{2} = \frac{{y - 1}}{2} = z\] và cách gốc tọa độ một khoảng lớn nhất.

Gợi ý: \[\overrightarrow n  = \left[ {\left[ {\overrightarrow {{u_d}} ;\overrightarrow {OA} } \right],\overrightarrow {{u_d}} } \right]\], phương trình mặt phẳng 11x – 16y + 10z – 53 = 0.

Ví dụ 3. Viết phương trình mặt phẳng (P) đi qua O, vuông góc với mặt phẳng (Q): \[2x - y + z - 1 = 0\] và cách điểm \[M\left( {\frac{1}{2};0;2} \right)\] một khoảng lớn nhất.

Gợi ý: Bản chất mp cần tìm vẫn đi qua đường thẳng cố định qua O và vuông góc với (P). Nến véctơ pháp tuyến của mặt phẳng cần tìm là \[\overrightarrow n  = \left[ {\left[ {\overrightarrow {{n_{(Q)}}} ,\overrightarrow {OM} } \right];\overrightarrow {{n_{(Q)}}} } \right]\].

Ví dụ 4: Tìm a để khoảng cách từ M (1;2;−2) đến mặt phẳng (P): \[(1 - a)x + (2 - 3a)y + az + 1 - a = 0\]lớn nhất.

Gợi ý: Ta có thể áp dụng công thức khoảng cách trực tiếp hoặc mp đã cho chứa đường thẳng cố định là d: \[\left\{ {\begin{array}{*{20}{c}}{x - 2y + 1 = 0}\\{ - x - 3y + z - 1 = 0}\end{array}} \right.\],  \[\overrightarrow {{u_d}}  = (2;1;5)\]và đi qua A(−1;0;0), do đó khoảng cách lớn nhất khi và chỉ khi \[{\overrightarrow n _P} = \left[ {\left[ {\overrightarrow {{u_d}} ;\overrightarrow {AM} } \right];\overrightarrow {{u_d}} } \right]\], từ đó ta tìm được a = 2.

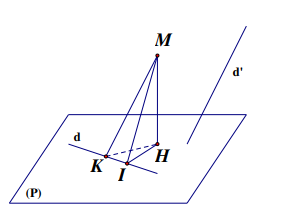
Bài toán 2: Viết phương trình mặt phẳng (P) chứa đường thẳng d, tạo với đường thẳng d’(d’ không song song với d) một góc lớn nhất.

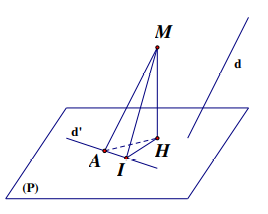
Giải: Lấy K là điểm thuộc d, vẽ đường thẳng KM song song với d’. Gọi H và I là hình chiếu vuông góc của M trên (P) và d.

Khi đó \[\sin \left( {d';(P)} \right) = \cos \widehat {KMH} = \frac{{MH}}{{KM}} \le \frac{{MI}}{{KM}}\].

Vậy góc giữa d và (P) lớn nhất khi và chỉ khi H trùng I, hay (P) là mặt phẳng nhận véctơ \[\overrightarrow {IM} \]làm véc tơ pháp tuyến, hay (P) là mặt phẳng chứa d và vuông góc với mặt phẳng chứa d , song song với d’.

Véc tơ pháp tuyến của mặt phẳng (P) cần tìm là \[\overrightarrow n  = \left[ {\left[ {\overrightarrow {{u_d}} ;\overrightarrow {{u_{d'}}} } \right];\overrightarrow {{u_d}} } \right]\].

Ví dụ 5: Viết phương trình mặt phẳng (P) chứa d: \[\frac{{x - 1}}{2} = \frac{{y + 1}}{1} = \frac{{z - 2}}{2}\] và tạo với đường thẳng d ′:\[\frac{{x + 1}}{1} = \frac{y}{2} = \frac{{z - 1}}{1}\] một góc lớn nhất.

Giải: Ta có \[\overrightarrow n  = \left[ {\left[ {\overrightarrow {{u_d}} ;\overrightarrow {{u_{d'}}} } \right];\overrightarrow {{u_d}} } \right] = (3; - 12;3)\]

(P) đi qua điểm A(1;−1;2) nên có phương trình \[(x - 1) - 4(y + 1) + (z - 2) = 0 \Leftrightarrow x - 4y + z - 7 = 0\]

Ví dụ 6: Viết phương trình mặt phẳng đi qua O và vuông góc với mặt phẳng (P): \[2x + y - z - 1 = 0\]và tạo với trục Oy một góc lớn nhất.

Gợi ý: Bản chất không thay đôi, mặt phẳng cần tìm có véc tơ pháp tuyến \[\overrightarrow n  = \left[ {\left[ {\overrightarrow {{n_P}} ,\overrightarrow j } \right];\overrightarrow {{n_P}} } \right] = ( - 2;5;1)\].

Vậy phương trình mặt phẳng cần tìm là 2x – 5y – z = 0.

Ví dụ 7: Viết phương trình mặt phẳng đi qua O, song song với đường thẳng d: \[\frac{{x - 1}}{2} = \frac{y}{1} = \frac{{z - 2}}{3}\] và tạo với mặt phẳng (P): x + 2y – z + 1 = 0 một góc nhỏ nhất.

Gợi ý: Bản chất bài toán toán vẫn là tìm phương trình mặt phẳng chứa đường thẳng a (qua O và song song với d) và tạo với đường thẳng b vuông góc với mp (P) một góc lớn nhất. Vậy véc tơ pháp tuyến mp (P) cần tìm là \[\overrightarrow n  = \left[ {\left[ {\overrightarrow {{u_d}} ;\overrightarrow {{n_P}} } \right];\overrightarrow {{u_d}} } \right] = ( - 12; - 27;17)\], nên phương trình mặt phẳng cần tìm là 12x + 27y – 17z = 0.

Ví dụ 8: Viết phương trình mặt phẳng đi qua hai điểm A(1;2;−1), B(2;1;3) và tạo với trục Ox một góc lớn nhất.

Gợi ý: Mặt phẳng cần tìm đi qua AB, cũng là mặt phẳng chứa đường thẳng AB cố định cho trước. Vậy \[\overrightarrow n  = \left[ {\left[ {\overrightarrow {AB} ,\overrightarrow i } \right];\overrightarrow {AB} } \right] = ( - 17; - 1;4)\]

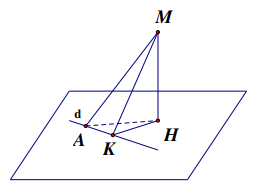
Bài toán 3: Viết phương trình đường thẳng d đi qua một điểm A cho trước và nằm trong mặt phẳng (P) cho trước và cách một điểm M cho trước một khoảng nhỏ nhất. (AM không vuông góc với (P)).

Giải: Gọi H và K lần lượt là hình chiếu vuông góc của M trên (P) và d. Dễ thấy ngay \[d(M;d) = MK \ge MH\]. Khoảng cách này nhỏ nhất khi và chỉ khi K ≡ H. Hay d là đường thẳng đi qua A và hình chiếu H của M trên (P).

Véc tơ chỉ phương của đường thẳng d cần tìm là \[\overrightarrow u  = \left[ {\left[ {\overrightarrow {{n_{(P)}}} ,\overrightarrow {AM} } \right];\overrightarrow {{n_{(P)}}} } \right]\].

Ví dụ 9: Viết phương trình đường thẳng d đi qua gốc tọa độ O, nằm trong mặt phẳng (P): 2x − y + z = 0 và cách điểm M (1;2;1) một khoảng nhỏ nhất.

Giải: Ta có véc tơ chỉ phương của đường thẳng cần tìm là \[\overrightarrow {{u_d}}  = \left[ {\left[ {\overrightarrow {{n_{(P)}}} ,\overrightarrow {OM} } \right];\overrightarrow {{n_{(P)}}} } \right] = ( - 4; - 13; - 5)\].

Vậy phương trình đường thẳng cần tìm là \[\frac{x}{4} = \frac{y}{{13}} = \frac{z}{5}\].

Ví dụ 10: Viết phương trình đường thẳng d đi qua điểm A(1;1;2), vuông góc với đường thẳng a: \[\frac{{x + 1}}{2} = \frac{y}{2} = \frac{{z - 3}}{4}\] và cách gốc tọa độ O một khoảng nhỏ nhất.

Gợi ý: Bản chất d vẫn là đường thẳng đi qua A và nằm trong mặt phẳng cố định (qua A và vuông góc với a).

Nên véc tơ chỉ phương vẫn là \[\overrightarrow {{u_d}}  = \left[ {\left[ {\overrightarrow {{u_a}} ,\overrightarrow {OA} } \right];\overrightarrow {{u_a}} } \right]\].

Ví dụ 11: Viết phương trình đường thẳng d đi qua O và song song với mặt phẳng (P):  2x – y – z + 1 = 0 và cách điểm M (1;−1;2) một khoảng nhỏ nhất.

Gợi ý: Bản chất d vẫn là đường thẳng đi qua O và nằm trong mặt phẳng cố định (qua O và song song với (P)).

Nên véc tơ chỉ phương vẫn là \[\overrightarrow {{u_d}}  = \left[ {\left[ {\overrightarrow {{n_{(P)}}} ,\overrightarrow {OM} } \right];\overrightarrow {{n_{(P)}}} } \right]\].

Ví dụ 12: Tìm cặp số nguyên dương (a, b) nhỏ nhất để khoảng cách từ O đến đường thẳng d: \[\left\{ {\begin{array}{*{20}{c}}{x = 1 + a + at}\\\begin{array}{l}y = 2 + b + bt\\z = 1 + 2a - b + (2a - b)t\end{array}\end{array}} \right.\](a ≠ 0) nhỏ nhất.

Gợi ý: Đường thẳng d đã cho đi qua điểm cố định A(1;2;1) và do \[\overrightarrow {{u_d}}  = (a;b;2a - b) \bot \overrightarrow n (2; - 1; - 1)\] nên d nằm trong mặt phẳng (P) qua A có véctơ pháp tuyến \[\overrightarrow n \].

Vậy véc tơ chỉ phương của đường thẳng cần tìm là \[\overrightarrow {{u_d}}  = \left[ {\left[ {\overrightarrow n ,\overrightarrow {OA} } \right];\overrightarrow n } \right] = ( - 8; - 11; - 5)\]. Vậy ta phải có \[\frac{a}{8} = \frac{b}{{11}} = \frac{{2a - b}}{5} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{a = 8}\\{b = 11}\end{array}} \right.\].

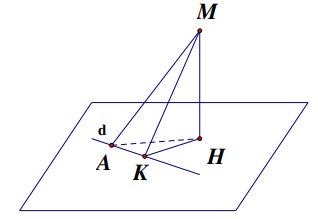
Bài toán 4: Viết phương trình đường thẳng d đi qua điểm A cho trước, nằm trong mặt phẳng (P) và cách điểm M (M khác A, MA không vuông góc với (P)) một khoảng lớn nhất.

Giải: Gọi H , K lần lượt là hình chiếu vuông góc của M trên (P) và d. Khi đó ta dế thấy \[d(M;d) = MK \le MA\], khoảng cách \[d(M;d)\] lớn nhất khi và chỉ khi K trùng A, hay d là đường thẳng nằm trong (P), đi qua A và vuông góc với AM.

Đường thẳng d cần tìm có véc tơ chỉ phương là \[\overrightarrow {{u_d}}  = \left[ {\overrightarrow {{n_{(P)}}} ,\overrightarrow {AM} } \right]\].

Ví dụ 13: Viết phương trình đường thẳng d đi qua điểm A(1;1;−1) cho trước, nằm trong mặt phẳng (P): 2x – y – z = 0 và cách điểm M (0;2;1) một khoảng lớn nhất.

Giải: Ta có véc tơ chỉ phương đường thẳng cần tìm là \[\overrightarrow u  = \left[ {\overrightarrow {AM} ,\overrightarrow {{n_{(P)}}} } \right] = (1;3; - 1)\].

Vậy phương trình đường thẳng cần tìm là \[\frac{{x - 1}}{1} = \frac{{y - 1}}{3} = \frac{{z + 1}}{{ - 1}}\].

Ví dụ 14: Viết phương trình đường thẳng d qua gốc tọa độ O, vuông góc với đường thẳng d₁: \[\frac{{x - 1}}{2} = \frac{y}{{ - 1}} = \frac{z}{{ - 2}}\] và cách điểm M (2;1;1) một khoảng lớn nhất.

Gợi ý: Véc tơ chỉ phương của đường thẳng cần tìm là \[\overrightarrow u  = \left[ {\overrightarrow {{u_{{d_1}}}} ,\overrightarrow {AM} } \right]\]

Ví dụ 15: Viết phương trình đường thẳng d đi qua điểm A(1;0;2), song song với mặt phẳng (P): 2x – y + z – 1 = 0 và cách gốc tọa độ O một khoảng lớn nhất.

Gợi ý: Véc tơ chỉ phương của đường thẳng cần tìm là \[\overrightarrow u  = \left[ {\overrightarrow {OA} ,\overrightarrow {{n_{(P)}}} } \right]\].

Ví dụ 16: Tìm a để đường thẳng d:  \[\left\{ {\begin{array}{*{20}{c}}{x = 1 - 2a + at}\\\begin{array}{l}y =  - 2 + 2a + (1 - a)t\\z = 1 + t\end{array}\end{array}} \right.\] ( a là tham số ) cách điểm \[M\left( {\frac{1}{2};1;4} \right)\]một khoảng lớn nhất.

Gợi ý: Dựa vào phương trình tham số của đường thẳng d đã cho, ta thấy d đi qua điểm cố định A(1;0;3) (ứng với t = 2) và vuông góc với đường thẳng có véc tơ chỉ phương \[\overrightarrow {{u_1}}  = (1;1; - 1)\]. Do đó véc tơ chỉ phương của đường thẳng d khi khoảng cách từ M đến nó lớn nhất là \[\overrightarrow {{u_d}}  = \left[ {\overrightarrow {{u_1}} ,\overrightarrow {AM} } \right] = \left( {2;\frac{{ - 1}}{2};\frac{3}{2}} \right)\] .

Vậy ta có: \[\frac{a}{2} = \frac{{1 - a}}{{\frac{{ - 1}}{2}}} = \frac{1}{{\frac{3}{2}}} \Leftrightarrow a = \frac{4}{3}\].

Bài toán 5: Cho mặt phẳng (P) và điểm A ∈ (P), và đường thẳng d (d cắt (P) và d không vuông góc với (P)). Viết phương trình đường thẳng d’ đi qua A, nằm trong (P) và tạo với d một góc nhỏ nhất.

Giải: Từ A vẽ đường thẳng AM//d. Gọi H, I lần lượt là hình chiếu vuông góc của M trên (P) và d’. Ta có

\[\cos \left( {d;d'} \right) = \cos \widehat {MAH} = \frac{{MH}}{{AM}} \le \frac{{MI}}{{MA}}\].

Vậy góc (d;d’) bé nhất khi và chỉ khi I trùng H. Hay d’ đi qua A và H, hay d’ đi qua A và song song với hình chiếu vuông góc của d trên (P).

Véc tơ chỉ phương của đường thẳng d’ cần tìm là \[\overrightarrow {{u_{d'}}}  = \left[ {\overrightarrow {{n_{(P)}}} ;\left[ {\overrightarrow {{n_{(P)}}} ,\overrightarrow {{u_d}} } \right]} \right]\].

Ví dụ 17: Viết phương trình đường thẳng đi qua gốc tọa độ O , nằm trong mặt phẳng (P): 2x + y – z = 0 và tạo với đường thẳng d: \[\frac{x}{2} = \frac{{y - 1}}{{ - 1}} = \frac{{z + 1}}{2}\] một góc nhỏ nhất.

Giải: Véc tơ chỉ phương của đường thẳng cần tìm là \[\overrightarrow {{u_a}}  = \left[ {\overrightarrow {{n_{(P)}}} ;\left[ {\overrightarrow {{n_{(P)}}} ,\overrightarrow {{u_d}} } \right]} \right] = ( - 10;7; - 13)\].

Vậy phương trình đường thẳng cần tìm là: \[\frac{x}{{ - 10}} = \frac{y}{7} = \frac{z}{{ - 13}}\].

Ví dụ 18: Viết phương trình đường thẳng đi qua O, vuông góc với đường thẳng d: \[\frac{{x - 1}}{2} = \frac{{y - 1}}{2} = \frac{{z + 1}}{1}\] và tạo với mặt phẳng (P): x – y + 2z – 1 = 0 một góc lớn nhất.

Gợi ý: Bản chất vẫn là Bài toán toán 5, với véc tơ chỉ phương của đường thẳng cần tìm là \[\overrightarrow u  = \left[ {\left[ {\overrightarrow {{u_d}} ;\overrightarrow {{n_{(P)}}} } \right];\overrightarrow {{u_d}} } \right]\]