Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Giải bài toán hình học không gian bằng phương pháp tọa độ, tài liệu bao gồm 37 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Giải bài toán hình học không gian bằng phương pháp tọa độ

GIẢI BÀI TOÁN HÌNH HỌC KHÔNG GIAN BẰNG PHƯƠNG PHÁP TỌA ĐỘ

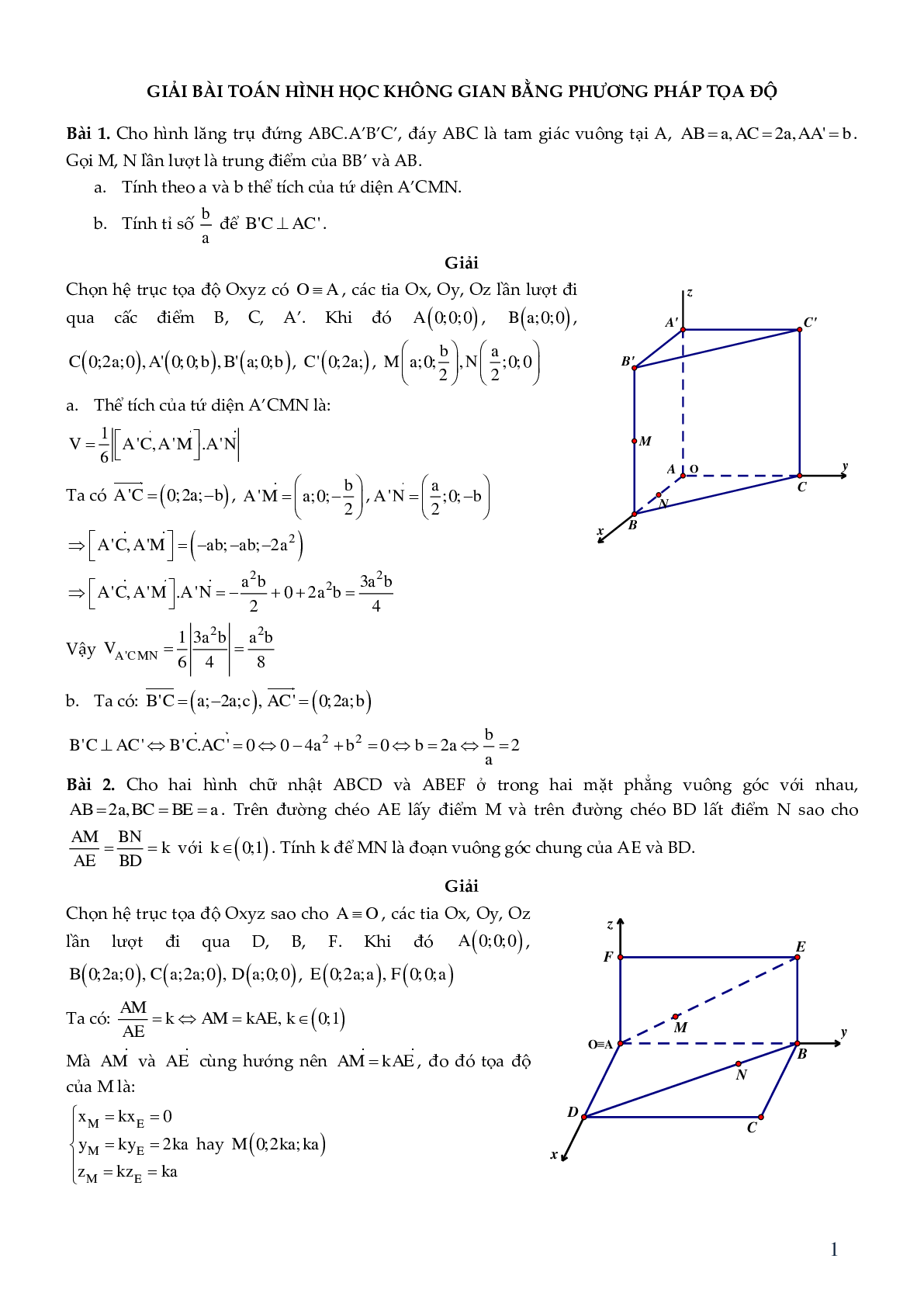
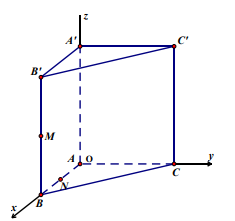
Bài 1. Cho hình lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông tại A, AB = a, AC = 2a, AA' = b. Gọi M, N lần lượt là trung điểm của BB’ và AB.

a. Tính theo a và b thể tích của tứ diện A’CMN.

b. Tính tỉ số \[\frac{b}{a}\] để B'C ^ AC'.

Giải

Chọn hệ trục tọa độ Oxyz có O º A, các tia Ox, Oy, Oz lần lượt đi qua các điểm B,C, A’. Khi đó \[A(0;0;0),\]\[B(a;0;0),\]\[C(0;2a;0),\]\[A'(0;0;b),\]

\[C'(0;2a;0),\]\[M\left( {a;0;\frac{b}{2}} \right),\]\[N\left( {\frac{a}{2};0;0} \right),\]

a. Thể tích của tứ diện A’CMN là:

\[V = \frac{1}{6}\left| {\left[ {\overrightarrow {A'C} ,\overrightarrow {A'M} } \right].\overrightarrow {A'N} } \right|\]

Ta có \[\overrightarrow {A'C}  = (0;2a; - b),\] \[\overrightarrow {A'M}  = \left( {a;0; - \frac{b}{2}} \right)\], \[\overrightarrow {A'N}  = \left( {\frac{a}{2};0; - b} \right)\]

\[ \Rightarrow \left[ {\overrightarrow {A'C} ,\overrightarrow {A'M} } \right] = ( - ab; - ab; - 2{a^2})\]

\[ \Rightarrow \left[ {\overrightarrow {A'C} ,\overrightarrow {A'M} } \right].\overrightarrow {A'N}  =  - \frac{{{a^2}b}}{2} + 0 + 2{a^2}b = \frac{{3{a^2}b}}{4}\]

Vậy \[{V_{A'CMN}} = \frac{1}{6}\left| {\frac{{3{a^2}b}}{4}} \right| = \frac{{{a^2}b}}{8}\]

b. Ta có : \[\overrightarrow {B'C}  = \left( {a; - 2a;c} \right),\]\[\overrightarrow {AC'}  = \left( {0;2a;b} \right)\]

\[\begin{array}{l}B'C \bot AC' \Leftrightarrow \overrightarrow {B'C} .\overrightarrow {AC'}  = 0 \Leftrightarrow 0 - 4{a^2} + {b^2} = 0\\ \Leftrightarrow b = 2a \Leftrightarrow \frac{b}{a} = 2\end{array}\]

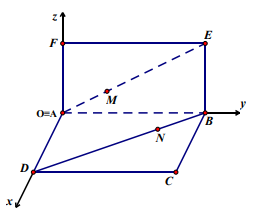
Bài 2. Cho hai hình chữ nhật ABCD và ABEF ở trong hai mặt phẳng vuông góc với nhau, AB = 2a,BC = BE = a. Trên đường chéo AE lấy điểm M và trên đường chéo BD lấy điểm N sao cho \[\frac{{AM}}{{AE}} = \frac{{BN}}{{BD}} = k\] với k Î (0;1). Tính k để MN là đoạn vuông góc chung của AE và BD.

 Giải

Chọn hệ trục tọa độ Oxyz sao cho A º O, các tia Ox, Oy, Oz lần lượt đi qua D, B, F. Khi đó \[A(0;0;0),\]\[B(0;2a;0),\]\[C(0;2a;0),\]\[D(a;0;0),\]\[E(0;2a;a),\]\[F\left( {0;2a;a} \right)\]

Ta có: \[\frac{{AM}}{{AE}} = k \Leftrightarrow AM = kAE,\] \[k \in (0;1)\]

Mà \[\overrightarrow {AM} \], \[\overrightarrow {AE} \]cùng hướng nên \[\overrightarrow {AM}  = k\overrightarrow {AE} \], do đó tọa độ của M là:

\[\left\{ {\begin{array}{*{20}{c}}{{x_M} = k{x_E} = 0}\\{{y_M} = k{y_E} = 2ka}\\{{z_M} = k{z_E} = ka}\end{array}} \right.\]hay \[M(0;2ka;ka)\]

Tương tự: \[\overrightarrow {BN}  = k\overrightarrow {BD} \]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_N} - 0 = k(a - 0)}\\{{y_N} - 2a = k(0 - a)}\\{{z_N} = 0 = k(0 - 0)}\end{array}} \right.;N(ka;2a - 2ka;0)\]

Ta có \[\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {MN}  = (ka;2a - 4ka; - ka)}\\{\overrightarrow {AE}  = (0;2a;a)}\\{\overrightarrow {BD}  = (a; - 2a;0)}\end{array}} \right.\]

MN là đoạn vuông góc chung của AE và BD \[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\overrightarrow {MN.} \overrightarrow {AE}  = 0}\\{\overrightarrow {MN} .\overrightarrow {BD}  = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{4{a^2} - 8k{a^2} - k{a^2} = 0}\\{k{a^2} - 4{a^2} + 8k{a^2} = 0}\end{array}} \right. \Leftrightarrow k = \frac{4}{9}\]

Vậy MN là đoạn vuông góc chung của AE và BD khi \[k = \frac{4}{9}\]

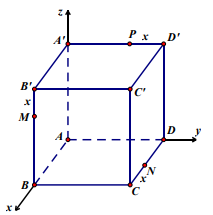
Bài 3. Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Trên các cạnh BB’,CD, A’D’ lần lượt lấy các điểm M, N, P sao cho B'M = CN = D'P = x, x Î(0;a) .

a. Chứng minh AC' ^ ( MNP) .

b. Xác định vị trí của M, N, P để tam giác MNP có diện tích bé nhất.

Giải

Chọn hệ trục tọa độ Oxyz có O º A, các tia Ox, Oy, Oz lần lượt đi qua các điểm B, D, A’. Khi đó \[A(0;0;0),\]\[B(a;0;0),\]\[C(a;a;0),\]\[D(0;a;0)\],\[A'(0;0;a),\]\[B'(a;0;a),C'(a;a;a)\]\[D'(0;a;a),M(a;0;a - x),N(a - x;a;0),P(0;a - x;a)\].

a. Ta có:

\[\overrightarrow {AC'}  = (a;a;a)\]

\[\overrightarrow {MN}  = ( - x;a; - a + x)\]

\[\overrightarrow {MP}  = ( - a;a - x;x)\]

\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\overrightarrow {AC'} .\overrightarrow {MN}  = 0}\\{\overrightarrow {AC'} .\overrightarrow {MP}  = 0}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\overrightarrow {AC'}  \bot \overrightarrow {MN} }\\{\overrightarrow {AC'}  \bot \overrightarrow {MP} }\end{array}} \right.\]

\[ \Rightarrow AC' \bot (MNP)\]  (đpcm)

b. Ta có \[MN = MP = NP = \sqrt {{x^2} + {a^2} + {{(a - x)}^2}}  = \sqrt {2{x^2} - 2ax + 2{a^2}} \]

\[ \Rightarrow \]Tam giác MNP là tam giác đều có cạnh bằng \[\sqrt 2 \sqrt {{x^2} - ax + {a^2}} \]

\[ \Rightarrow \]Diện tích của tam giác MNP là: \[S = \frac{{M{N^2}.\sqrt 3 }}{4} = \frac{{\sqrt 3 }}{2}\left( {{x^2} - ax + {a^2}} \right)\]

hay \[S = \frac{{\sqrt 3 }}{2}\left[ {{{\left( {x - \frac{a}{2}} \right)}^2} + \frac{{3{a^2}}}{4}} \right] \ge \frac{{3{a^2}\sqrt 3 }}{8}\]

Dấu “=” xảy ra \[ \Leftrightarrow x = \frac{a}{2}\]

Vậy min(S) = \[\frac{{3{a^2}\sqrt 3 }}{8}\]khi M, N, P lần lượt là trung điểm của các cạnh BB’, CD, A’D’.

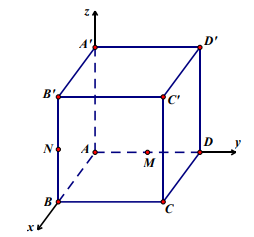
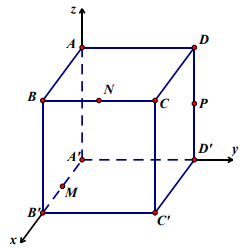
Bài 4. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi M và N lần lượt là trung điểm của AD và BB’. Chứng minh AC' ^ (AB’D’) và tính thể tích của khối tứ diện A’CMN.

Giải

Chọn hệ trục tọa độ Oxyz có như hình vẽ, ta có: \[A(0;0;0),\]\[B(a;0;0),\]\[C(a;a;0),\]\[D(0;a;0)\],\[A'(0;0;a),\]\[B'(a;0;a),C'(a;a;a)\], \[D'(0;a;a)\].

a. Ta có: \[\overrightarrow {A'C}  = (a;a; - a),\]\[\overrightarrow {AB'}  = (a;0;a),\]\[\overrightarrow {AD'}  = (0;a;a)\].

\[ \Rightarrow \overrightarrow {A'C.} \overrightarrow {AB'}  = 0\]và \[\overrightarrow {A'C.} \overrightarrow {AD'}  = 0\]

\[ \Rightarrow A'C \bot AB'\]và \[A'C \bot AD'\]

\[ \Rightarrow A'C \bot (AB'D')\] (đpcm)

b. Thể tích của tứ diện A’CMN là:

\[V = \frac{1}{6}\left| {\left[ {\overrightarrow {A'N} ,\overrightarrow {A'M} } \right].\overrightarrow {A'C} } \right|\]

Ta có \[N = \left( {a;0;\frac{a}{2}} \right)\],\[M = \left( {0;\frac{a}{2};0} \right)\]

\[ \Rightarrow \]\[\overrightarrow {A'N}  = \left( {a;0; - \frac{a}{2}} \right)\], \[\overrightarrow {A'M}  = \left( {0;\frac{a}{2}; - a} \right)\] và \[\overrightarrow {A'C}  = (a;a; - a)\]

\[ \Rightarrow \left[ {\overrightarrow {A'N} ,\overrightarrow {A'M} } \right] = (\frac{{{a^2}}}{4};{a^2};\frac{{{a^2}}}{2})\]

và \[\left[ {\overrightarrow {A'N} ,\overrightarrow {A'M} } \right].\overrightarrow {A'C}  = \frac{{{a^3}}}{4} + {a^3} - \frac{{{a^3}}}{2} = \frac{{3{a^3}}}{4}\]

Vậy \[V = \frac{1}{6}.\frac{{3{a^3}}}{4} = \frac{{{a^3}}}{4}\] (đvtt)

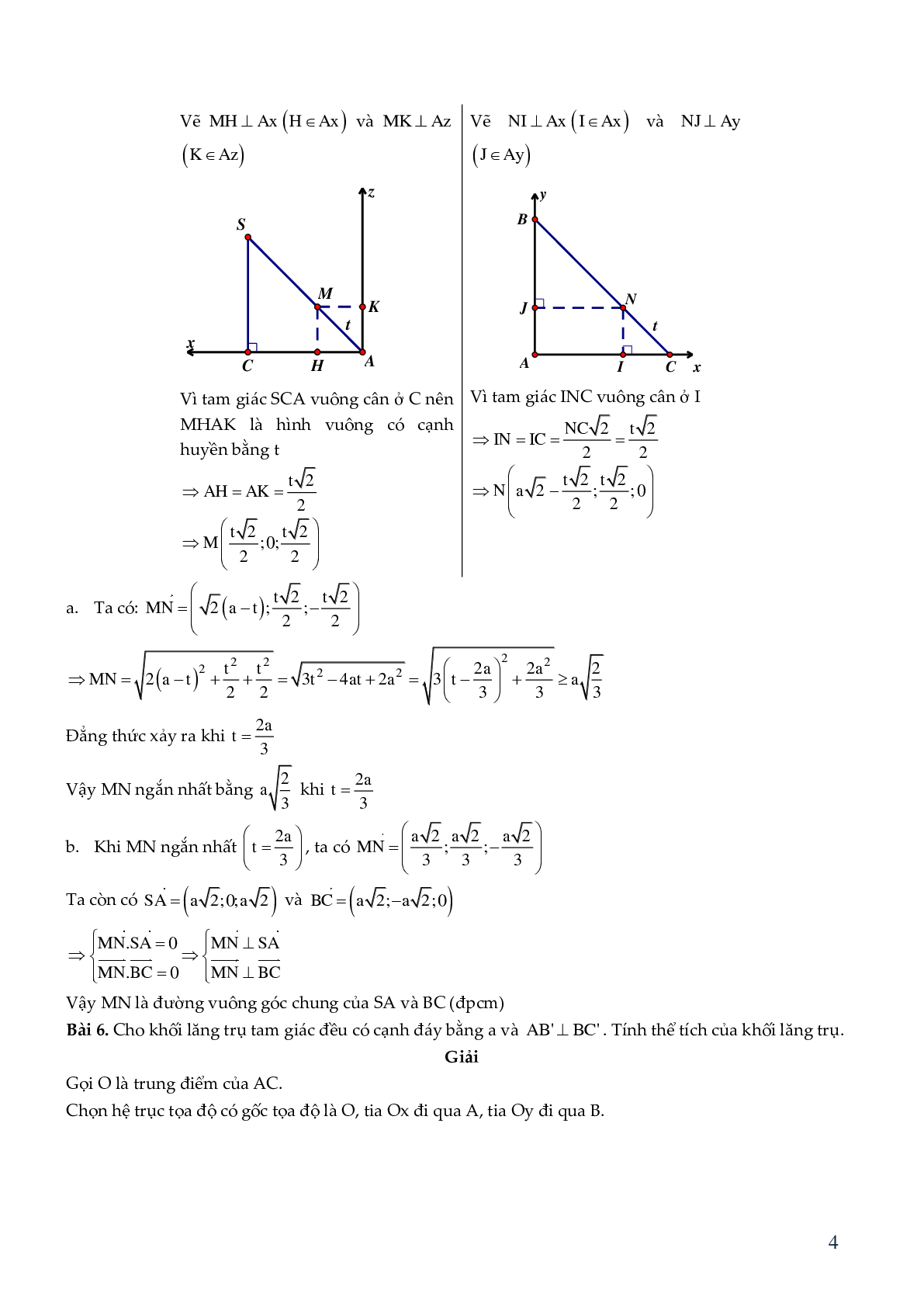
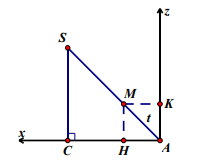
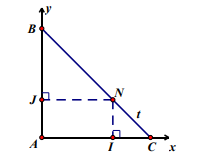
Bài 5. Cho tứ diện SABCD có SC = CA = AB = \[a\sqrt 2 \], SC \[ \bot \] (ABC), tam giác ABC vuông tại A. Các điểm M \[ \in \]SA, N\[ \in \]BC sao cho AM = Cn = t (0 < t < 2a). Tính t để MN ngắn nhất. Trong trường hợp này chứng minh MN là đoạn vuông góc chung của BC và SA đồng thời tính thể tích của khối tứ diện ABMN.

Giải

Chọn hệ trục tọa độ Oxyz sao cho A º O (0;0;0), tia Ox chứa AC, tia Oy chứa AB và tia Oz cùng hướng với vectơ \[\overrightarrow {CS} \]. Khi đó ta có  \[A(0;0;0),\]\[B(0;a\sqrt 2 ;0),\]\[C(a\sqrt 2 ;0;0),\]\[S(a\sqrt 2 ;0;a\sqrt 2 )\].

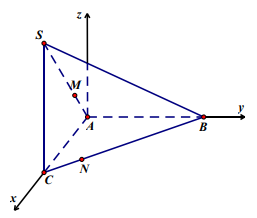
Vẽ MH \[ \bot \]Ax (H\[ \in \]Ax) và MK \[ \bot \]Az (K \[ \in \]Az)

Vì tam giác SCA vuông cân ở C nên MHAK là hình vuông có cạnh huyền bằng t

\[\begin{array}{l} \Rightarrow AH = AK = \frac{{t\sqrt 2 }}{2}\\ \Rightarrow M\left( {\frac{{t\sqrt 2 }}{2};0;\frac{{t\sqrt 2 }}{2}} \right)\end{array}\]

Vẽ NI \[ \bot \]Ax (I\[ \in \]Ax) và NJ \[ \bot \]Ay (J \[ \in \]Ay)

Vì tam giác INC vuông cân ở I

\[\begin{array}{l} \Rightarrow IN = IC = \frac{{NC\sqrt 2 }}{2} = \frac{{t\sqrt 2 }}{2}\\ \Rightarrow N\left( {a\sqrt 2  - \frac{{t\sqrt 2 }}{2};\frac{{t\sqrt 2 }}{2};0} \right)\end{array}\]

a. Ta có : \[\overrightarrow {MN}  = \left( {\sqrt 2 (a - t);\frac{{t\sqrt 2 }}{2}; - \frac{{t\sqrt 2 }}{2}} \right)\]

\[\begin{array}{l} \Rightarrow MN = \sqrt {2{{\left( {a - t} \right)}^2} + \frac{{{t^2}}}{2} + \frac{{{t^2}}}{2}} \\ = \sqrt {3{t^2} - 4at + 2{a^2}} \\ = \sqrt {3{{\left( {t - \frac{{2a}}{3}} \right)}^2} + \frac{{2{a^2}}}{3}}  \ge a\sqrt {\frac{2}{3}} \end{array}\]

Đẳng thức xảy ra khi \[t = \frac{{2a}}{3}\]

Vậy MN ngắn nhất bằng \[a\sqrt {\frac{2}{3}} \]khi \[t = \frac{{2a}}{3}\].

b. Khi MN ngắn nhất (\[t = \frac{{2a}}{3}\]), ta có \[\overrightarrow {MN}  = \left( {\frac{{a\sqrt 2 }}{3};\frac{{a\sqrt 2 }}{3}; - \frac{{a\sqrt 2 }}{3}} \right)\]

Ta còn có \[\overrightarrow {SA}  = (a\sqrt 2 ;0;a\sqrt 2 )\]và \[\overrightarrow {BC}  = (a\sqrt 2 ; - a\sqrt 2 ;0)\]

\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\overrightarrow {MN} .\overrightarrow {SA}  = 0}\\{\overrightarrow {MN} .\overrightarrow {BC}  = 0}\end{array} \Rightarrow } \right.\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {MN}  \bot \overrightarrow {SA} }\\{\overrightarrow {MN}  \bot \overrightarrow {BC} }\end{array}} \right.\]

Vậy MN là đường vuông góc chung của SA và BC (đpcm)

Bài 6. Cho khối lăng trụ tam giác đều có cạnh đáy bằng a và AB'^BC’. Tính thể tích của khối lăng trụ.

Giải

Gọi O là trung điểm của AC.

Chọn hệ trục tọa độ có gốc tọa độ là O, tia Ox đi qua A, tia Oy đi qua B.

Khi đó \[A\left( {\frac{a}{2};0;0} \right)\], \[B\left( {0;\frac{{a\sqrt 3 }}{2};0} \right)\],\[C\left( { - \frac{a}{2};0;0} \right)\],

\[B'\left( {0;\frac{{a\sqrt 3 }}{2};h} \right)\],\[C'\left( { - \frac{a}{2};0;h} \right)\]

(\[h = AA' = BB' = ...\])

Ta có \[\overrightarrow {AB'}  = \left( { - \frac{a}{2};\frac{{a\sqrt 3 }}{2};h} \right)\]và \[\overrightarrow {BC'}  = \left( { - \frac{a}{2}; - \frac{{a\sqrt 3 }}{2};h} \right)\]

\[\begin{array}{l}AB' \bot BC' \Leftrightarrow \overrightarrow {AB'} .\overrightarrow {BC'}  = 0\\ \Leftrightarrow \frac{{{a^2}}}{4} - \frac{{3{a^2}}}{4} + {h^2} = 0 \Leftrightarrow h = \frac{{a\sqrt 2 }}{2}\end{array}\]

Vậy thể tích của khối lăng trụ là \[V = {S_{\Delta ABC}}.h = \frac{{{a^2}\sqrt 3 }}{4}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 6 }}{8}\]

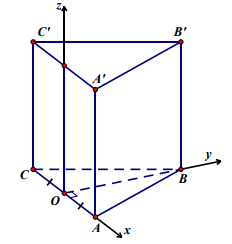
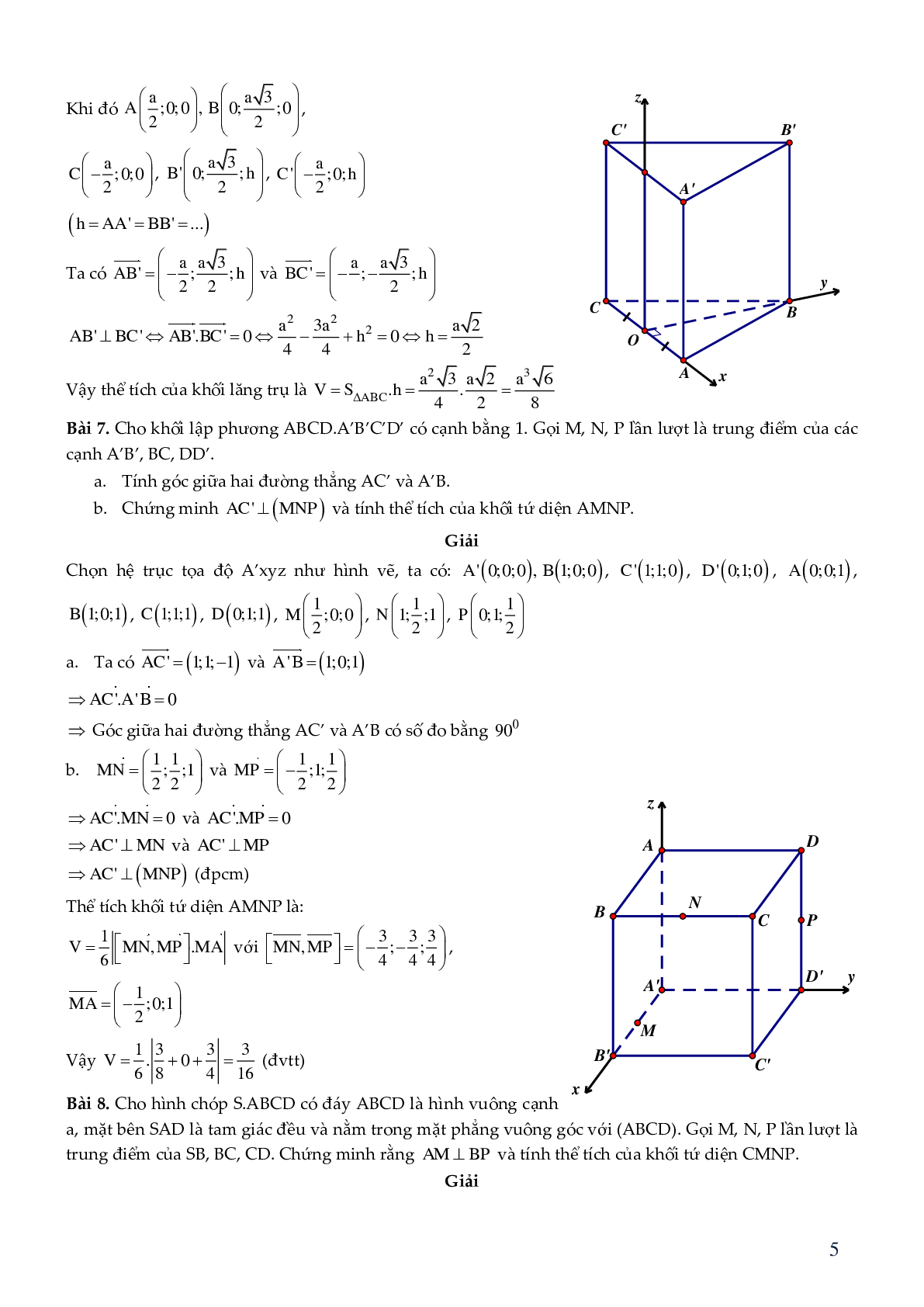
Bài 7. Cho khối lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm của các cạnh A’B’, BC, DD’.

a. Tính góc giữa hai đường thẳng AC’ và A’B.

b. Chứng minh AC' ^ (MNP) và tính thể tích của khối tứ diện AMNP.

Giải

Chọn hệ trục tọa độ A’xyz như hình vẽ, ta có: \[A'(0;0;0),B'(1;0;0),C'(1;1;0),\]\[D'(0;1;0),A(0;0;1),\]\[B(1;0;1),C(1;1;1),D(0;1;1),\]

\[M\left( {\frac{1}{2};0;0} \right),N\left( {1;\frac{1}{2};1} \right),P\left( {0;1;\frac{1}{2}} \right)\]

a. Ta có \[\overrightarrow {AC'}  = (1;1; - 1)\]và \[\overrightarrow {A'B}  = (1;0;1)\]

\[ \Rightarrow \overrightarrow {AC'} .\overrightarrow {A'B}  = 0\]

\[ \Rightarrow \]Góc giữa hai đường thẳng AC’ và A’B có số đo bằng 90⁰

b. \[\overrightarrow {MN}  = \left( {\frac{1}{2};\frac{1}{2};1} \right)\]và \[\overrightarrow {MP}  = \left( { - \frac{1}{2};1;\frac{1}{2}} \right)\]

\[ \Rightarrow \overrightarrow {AC'} .\overrightarrow {MN}  = 0\]và \[\overrightarrow {AC'} .\overrightarrow {MP}  = 0\]

\[ \Rightarrow \]\[AC' \bot MN\]và \[AC' \bot MP\]

\[ \Rightarrow AC' \bot (MNP)\]

Thể tích khối tứ diện AMNP là:

\[V = \frac{1}{6}\left| {\left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right].\overrightarrow {MA} } \right|\]

với \[\left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right] = \left( { - \frac{3}{4}; - \frac{3}{4};\frac{3}{4}} \right)\], \[\overrightarrow {MA}  = \left( { - \frac{1}{2};0;1} \right)\]

Vậy \[V = \frac{1}{6}\left| {\frac{3}{8} + 0 + \frac{3}{4}} \right| = \frac{3}{{16}}\]  (đvtt)

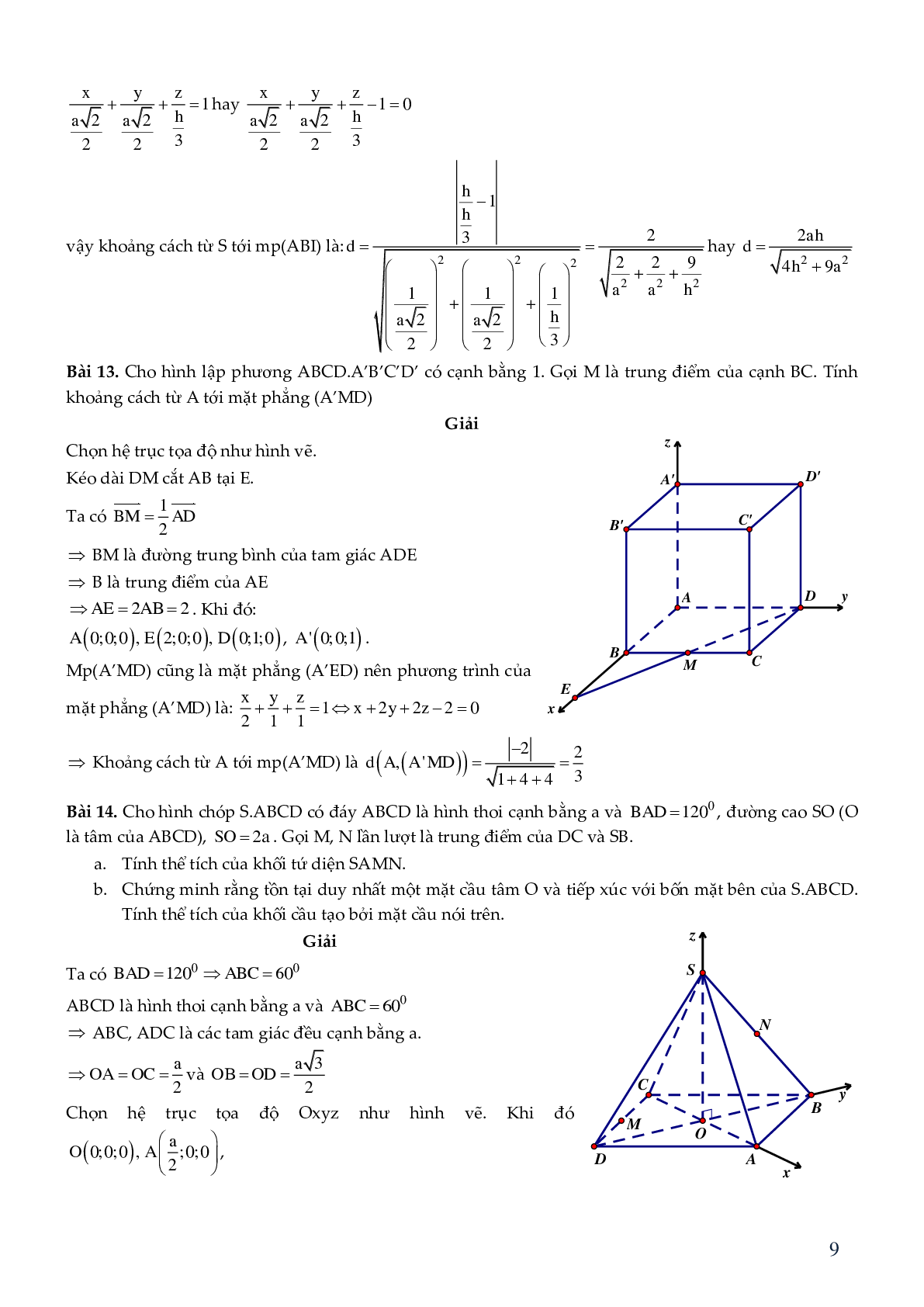
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAD là tam giác đều và nằm trong mặt phẳng vuông góc với (ABCD). Gọi M, N, P lần lượt là trung điểm của SB, BC, CD. Chứng minh rằng AM ^ BP và tính thể tích của khối tứ diện CMNP.