Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết và bài tập ôn tập chương phương pháp tọa độ trong không gian, tài liệu bao gồm 25 trang gồm có lý thuyết và bài tập. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Lý thuyết và bài tập ôn tập chương phương pháp tọa độ trong không gian

TỌA ĐỘ ĐIỂM – TỌA ĐỘ VECTO

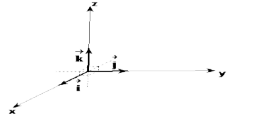
I. Hệ trục tọa độ Oxyz: Gồm 3 trục x’Ox, y’Oy, z’Oz vuông góc từng đôi tại điểm O.

\[\left| {\overrightarrow i } \right| = \left| {\overrightarrow j } \right| = \left| {\overrightarrow k } \right| = 1\], \[\overrightarrow i .\overrightarrow j  = \overrightarrow i .\overrightarrow k  = \overrightarrow j .\overrightarrow k  = 0\]

\[\overrightarrow i  = (1;0;0)\], \[\overrightarrow j  = (0;1;0)\], \[\overrightarrow k  = (0;0;1)\]

\[\overrightarrow 0  = (0;0;0)\]

II. Tọa độ vecto

Định nghĩa:

\[\overrightarrow u  = (x;y;z) \Leftrightarrow \overrightarrow u  = x\overrightarrow i  + y\overrightarrow j  + z\overrightarrow k \]

Công thức:

Trong không gian Oxyz, cho: \[\overrightarrow a  = ({a_1};{a_2};{a_3})\], \[\overrightarrow b  = ({b_1};{b_2};{b_3})\]

1. Tọa độ vecto tổng:

\[\overrightarrow a  \pm \overrightarrow b  = ({a_1} \pm {b_1};{a_2} \pm {b_2};{a_3} \pm {b_3})\]

2. Tích của 1 số thực k với 1 vecto:

\[k.\overrightarrow a  = (k{a_1};k{a_2};k{a_3})\]   (\[k \in R\])

3. Hai vecto bằng nhau:

\[\overrightarrow a  = \overrightarrow b  \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{a_1} = {b_1}}\\{{a_2} = {b_2}}\\{{a_3} = {b_3}}\end{array}} \right.\]

4. Điều kiện 2 vecto cùng phương:

\[\overrightarrow a \],\[\overrightarrow b \] cùng phương \[ \Leftrightarrow \overrightarrow a  = k.\overrightarrow b ;\overrightarrow b  \ne \overrightarrow 0 \]

\[ \Leftrightarrow \exists k \in R:\left\{ {\begin{array}{*{20}{c}}{{a_1} = k{b_1}}\\{{a_2} = k{b_2}}\\{{a_3} = k{b_3}}\end{array}} \right.\]

5. Biểu thức tọa độ của tích vô hướng

\[\overrightarrow a .\overrightarrow b  = {a_1}.{b_1} + {a_2}.{b_2} + {a_3}.{b_3}\]

6. Độ dài vecto:

\[\left| {\overrightarrow a } \right| = \sqrt {a_1^2 + a_2^2 + a_3^2} \]

7. Điều kiện 2 vecto vuông góc

\[\overrightarrow a  \bot \overrightarrow b  = \overrightarrow a .\overrightarrow b  = 0 \Leftrightarrow {a_1}.{b_1} + {a_2}.{b_2} + {a_3}.{b_3} = 0\]

8. Góc giữa 2 vecto \[\overrightarrow a  \ne \overrightarrow 0 \], \[\overrightarrow b  \ne \overrightarrow 0 \]: Gọi \[\varphi  = (\overrightarrow a ,\overrightarrow b )\]

\[\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{{a_1}.{b_1} + {a_2}.{b_2} + {a_3}.{b_3}}}{{\sqrt {a_1^2 + a_2^2 + a_3^2} .\sqrt {b_1^2 + b_2^2 + b_3^2} }}\]

Tích có hướng của 2 vecto

Định nghĩa: Không gian Oxyz cho \[\overrightarrow a  = ({a_1};{a_2};{a_3}),\overrightarrow b  = ({b_1};{b_2};{b_3})\]

\[\overrightarrow v  = \left[ {\overrightarrow a ,\overrightarrow b } \right] = \left( {\left| {\begin{array}{*{20}{c}}{{a_2}}&{{a_3}}\\{{b_2}}&{{b_3}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{{a_3}}&{{a_1}}\\{{b_3}}&{{b_1}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{{a_1}}&{{a_2}}\\{{b_1}}&{{b_2}}\end{array}} \right|} \right)\]

Tính chất

\[\left[ {\overrightarrow a ,\overrightarrow b } \right] \bot \overrightarrow a \]

\[\left[ {\overrightarrow a ,\overrightarrow b } \right] \bot \overrightarrow b \]

\[\left| {\left[ {\overrightarrow a ,\overrightarrow b } \right]} \right| = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\sin (\overrightarrow a ,\overrightarrow b )\]

\[\overrightarrow a ,\overrightarrow b \] cùng phương \[ \Leftrightarrow \left[ {\overrightarrow a ,\overrightarrow b } \right] = \overrightarrow 0 \]

Điều kiện đồng phẳng của ba vecto:

\[\overrightarrow a ,\overrightarrow b \] và \[\overrightarrow c \]đồng phẳng \[ \Leftrightarrow \left[ {\overrightarrow a ,\overrightarrow b } \right].\overrightarrow c  = 0\]

III. Tọa độ điểm

a. Định nghĩa : \[M(x;y;z)\]\[ \Leftrightarrow \overrightarrow {OM}  = x\overrightarrow i  + y\overrightarrow j  + z\overrightarrow k \]

\[M \in Ox \Rightarrow M(x;0;0)\]

\[M \in Oy \Rightarrow M(0;y;0)\]

\[M \in Oz \Rightarrow M(0;0;z)\]

\[M \in (Oxy) \Rightarrow M(x;y;0)\]

\[M \in (Oyz) \Rightarrow M(0;y;z)\]

\[M \in (Oxz) \Rightarrow M(x;0;z)\]

b. Công thức

Cho các điểm \[A({x_A};{y_A};{z_A})\], \[B({x_B};{y_B};{z_B})\], …

1. Tọa độ vecto: \[\overrightarrow {AB}  = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\]

2. Khoảng cách giữa 2 điểm A, B (độ dài đoạn thẳng AB)

\[AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2} + {{({z_B} - {z_A})}^2}} \]

3. Tọa độ trung điểm của đoạn thẳng:

M là trung điểm của đoạn AB

\[M(\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\]

4. Tọa độ trọng tâm tam giác

G trọng tâm tam giác ABC

\[G = (\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\]

Một số ứng dụng và công thức

1. Chứng minh 3 điểm A, B, C thẳng hàng; không thẳng hàng

3 điểm A, B, C thẳng hàng \[ \Leftrightarrow \overrightarrow {AB}  = k\overrightarrow {AC} \] hoặc

3 điểm A, B, C thẳng hàng \[ \Leftrightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \overrightarrow 0 \]

3 điểm A, B, C không thẳng hàng \[ \Leftrightarrow \overrightarrow {AB}  \ne k\overrightarrow {AC} \]hoặc

3 điểm A, B, C không thẳng hàng \[ \Leftrightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] \ne \overrightarrow 0 \]

2. D (x;y;z) là đỉnh hình bình hành ABCD \[ \Leftrightarrow \overrightarrow {AD}  = \overrightarrow {BC} \]

3. Diện tích hình bình hành ABCD:\[{S_{ABCD}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right]} \right|\] hoặc\[{S_{ABCD}} = 2{S_{\Delta ABC}}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right|\]

4. Diện tích tam giác ABC: \[{S_{\Delta ABC}} = \frac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right|\]

5. Chứng minh 4 điểm A,B,C,D đồng phẳng, không đồng phẳng

4 điểm A,B,C,D đồng phẳng \[ \Leftrightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD}  = 0\]

4 điểm A,B,C,D không đồng phẳng

 \[ \Leftrightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD}  \ne 0\] (A,B,C,D là đỉnh tứ diện ABCD)

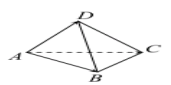
6. Thể tı́ch tứ diện ABCD:

\[{V_{ABCD}} = \frac{1}{6}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} } \right|\]

7. Tính thể tích hình hộp ABCD.A’B’C’D’:

\[{V_{ABCD.A'B'C'D'}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AA'} } \right|\]

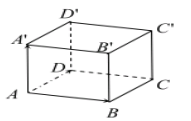
Khoảng cách

8. Khoảng cách giữa 2 điểm A,B (độ dài đoan thẳng AB):

\[AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2} + {{({z_B} - {z_A})}^2}} \]

9. Khoảng cách từ điểm M (x₀;y₀;z₀) đến mặt phẳng (α) : Ax + By + Cz + D = 0

\[d(M,(\alpha )) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\]

Nếu 2 mp song song :

 \[(\alpha )//(\beta ) \Rightarrow d\left( {(\alpha ),(\beta )} \right) = d\left( {M \in (\alpha ),(\beta )} \right) = d\left( {N \in (\beta ),(\alpha )} \right)\]

Nếu đường thẳng song song mp:

\[\begin{array}{l}\Delta //mp(\alpha )\\ \Rightarrow d\left( {\Delta ;(\alpha )} \right) = d\left( {M \in (\alpha )} \right)\\ = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\end{array}\]

10. Khoảng cách từ điểm M (x₀;y₀;z₀) đến đường thẳng \[\Delta \]:

Đường thẳng \[\Delta \]: \[\left\{ {\begin{array}{*{20}{c}}{qua{M_0}}\\{VTCP:\overrightarrow u }\end{array}} \right.\]

\[d(M;\Delta ) = \frac{{\left| {\left[ {\overrightarrow {{M_0}M} ,\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}}\]

Nếu 2 đường thẳng song song:

\[{\Delta _1}//{\Delta _2} \Rightarrow d({\Delta _1};{\Delta _2}) = d({M_1} \in {\Delta _1};{\Delta _2}) = d({M_2} \in {\Delta _2};{\Delta _1})\]

11. Khoảng cách giữa 2 đường thẳng chéo nhau:

Đường thẳng \[{\Delta _1},{\Delta _2}\]chéo nhau.

\[{\Delta _1}:\left\{ {\begin{array}{*{20}{c}}{qua{M_1}}\\{VTCP:\overrightarrow {{u_1}} }\end{array}} \right.\];  \[{\Delta _2}:\left\{ {\begin{array}{*{20}{c}}{qua{M_2}}\\{VTCP:\overrightarrow {{u_2}} }\end{array}} \right.\]

\[d({\Delta _1};{\Delta _2}) = \frac{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}} } \right|}}{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right]} \right|}};\]

Công thức góc

\[\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \]VTPT của 2 mặt phẳng. Gọi \[\varphi  = (\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} )\]

\[\cos \varphi  = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\]

14. Góc giữa 2 đường thẳng:

\[\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \]là VTCP của 2 đường thẳng. Gọi \[\varphi  = \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right)\]

\[\cos \varphi  = \frac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}}\]

15. Góc giữa đường thẳng; mặt phẳng:

\[\overrightarrow n \]là VTPT mp; \[\overrightarrow u \]là VTCP đường thẳng. Gọi \[\varphi  = \left( {\overrightarrow n ,\overrightarrow u } \right)\]

\[\sin \varphi  = \frac{{\left| {\overrightarrow n .\overrightarrow u } \right|}}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow u } \right|}}\]

Bài tập: Tìm tọa độ vectơ, tọa độ điểm thuộc đường – Mặt

Câu 1: Cho \[\overrightarrow u  = (1; - 2;3),\overrightarrow v  = 2\overrightarrow i  + 2\overrightarrow j  - \overrightarrow k \]. Toa đô ̣ vecto \[\overrightarrow x  = \overrightarrow u  - \overrightarrow v \]

A. \[\overrightarrow x  = (3;0;2)\]

B. \[\overrightarrow x  = (1; - 4; - 4)\]

C. \[\overrightarrow x  = ( - 1;4;4)\]

D. \[\overrightarrow x  = (2; - 4; - 3)\]

Câu 2: Cho \[\overrightarrow v  = 2\overrightarrow i  + 2\overrightarrow j  - \overrightarrow k ;\overrightarrow w  = 4\overrightarrow j  - 4\overrightarrow k \]. Toa đô ̣vecto \[\overrightarrow u  = \overrightarrow v  + 3\overrightarrow w \]

A. \[\overrightarrow u  = (2;6; - 5)\]

B. \[\overrightarrow u  = (2;14; - 13)\]

C. \[\overrightarrow u  = (2; - 14;13)\]

D. \[\overrightarrow u  = ( - 2;14;13)\]

Câu 3: Cho \[\overrightarrow u  = (1;2;3),\overrightarrow v  = 2\overrightarrow i  + 2\overrightarrow j  - \overrightarrow k ;\overrightarrow w  = 4\overrightarrow j  - 4\overrightarrow k \].Toa độ vecto \[\overrightarrow x  = 2\overrightarrow u  + 4\overrightarrow v  - 3\overrightarrow w \]

A. \[\overrightarrow x  = ( - 2;12;17)\]

B. \[\overrightarrow x  = (2; - 12; - 17)\]

C. \[\overrightarrow x  = (7;4; - 2)\]

D. \[\overrightarrow x  = (2; - 12;1)\]

Câu 4: Cho \[\overrightarrow a  = (1; - 1;1),\overrightarrow b  = (3;0; - 1),\overrightarrow c  = (3;2; - 1)\]. Tìm tọa độ của vectơ \[\overrightarrow u  = (\overrightarrow a .\overrightarrow b ).\overrightarrow c \]

A. (2; 2;–1)

B. (6; 0; 1)

C. (5; 2; –2)

D. (6; 4; –2)

Câu 5: Tính góc giữa hai vectơ \[\overrightarrow a  = ( - 2; - 1;2),\overrightarrow b  = (0;1; - 1)\]

A. 135°

B. 90°

C. 60°

D. 45°

Câu 6: Trong k.g Oxyz, cho 3 vectơ \[\overrightarrow a  = ( - 1;1;0),\overrightarrow b  = (1;1;0),\overrightarrow c  = (1;1;1)\]. Trong các mệnh đề sau, mệnh đề nào sai

A. \[\left| {\overrightarrow a } \right| = \sqrt 2 \]

B. \[\left| {\overrightarrow c } \right| = \sqrt 3 \]

C. \[\overrightarrow a  \bot \overrightarrow b \]

D. \[\overrightarrow b  \bot \overrightarrow c \]

Câu 7: Trong k.g Oxyz, cho 3 vectơ \[\overrightarrow a  = ( - 1;1;0),\overrightarrow b  = (1;1;0),\overrightarrow c  = (1;1;1)\]. Trong các mệnh đề sau, mệnh đề nào đúng

A. \[\overrightarrow a .\overrightarrow c  = 1\]

B. \[\overrightarrow a \] và \[\overrightarrow b \] cùng phương

C. \[\cos (\overrightarrow b ,\overrightarrow c ) = \frac{2}{{\sqrt 6 }}\]

D. \[\overrightarrow a  + \overrightarrow b  + \overrightarrow c  = \overrightarrow 0 \]

Câu 8 : Cho \[\overrightarrow a  = (3;2;1),\overrightarrow b  = ( - 2;2; - 4)\], \[\left| {\overrightarrow a  - \overrightarrow b } \right|\] bằng :

A. 50

B. \[2\sqrt 5 \]

C. 3

D. \[5\sqrt 2 \]

Câu 9 : Cho \[\overrightarrow a  = (3; - 1;2),\overrightarrow b  = (4;2; - 6)\]. Tính \[\left| {\overrightarrow a  + \overrightarrow b } \right|\]

A. 8

B. 9

C. \[\sqrt {65} \]

D. \[5\sqrt 2 \]

Câu 10: Cho \[\overrightarrow a  = (2; - 1;2)\]. Tìm y, z sao cho \[\overrightarrow c  = ( - 2;y;z)\]cùng phương với \[\overrightarrow a \]

A. y = –1; z = 2

B. y = 2; z = –1

C. y = 1; z = –2

D. y = –2; z = 1

Câu 11: Cho A(2;5;3); B(3;7;4); C(x;y;6) .Tı̀m x, y để 3 điểm A,B,C thẳng hàng.

A. x = 5; =11

B. x = 11; y = 5

C. x = - 5; y = 11

D. x = 5; y = - 11

Câu 12: Trong không gian Oxyz cho ba điểm A(2;-3;4), B(1;y;-1), C(x;4;3). Nếu 3 điểm A, B, C thẳng hàng thì vai trò của 5x + y bằng :

A. 36

B. 40

C. 42

D. 41

Câu 13: Cho vectơ \[\overrightarrow a  = (2; - 1;0)\].Tı̀m toa độ vecto \[\overrightarrow b \] cùng phương với vectơ \[\overrightarrow a \], biết rằng \[\overrightarrow a .\overrightarrow b  = 10\].

A. \[\overrightarrow b  = (4; - 2;0)\]

B. \[\overrightarrow b  = ( - 4;2;0)\]

C. \[\overrightarrow b  = (4;2;0)\]

D. \[\overrightarrow b  = ( - 2;4;0)\]

Câu 14: Cho vectơ \[\overrightarrow a  = (2\sqrt 2 ; - 1;4)\]. Tı̀m toa độ vecto \[\overrightarrow b \] cùng phương với vectơ \[\overrightarrow a \], biết rằng \[\left| {\overrightarrow b } \right| = 10\].

A. \[\left[ {\begin{array}{*{20}{c}}{\overrightarrow b  = (4\sqrt 2 ;2; - 8)}\\{\overrightarrow b  = ( - 4\sqrt 2 ;2; - 8)}\end{array}} \right.\]

B. \[\left[ {\begin{array}{*{20}{c}}{\overrightarrow b  = (4\sqrt 2 ; - 2;8)}\\{\overrightarrow b  = (4\sqrt 2 ;2;8)}\end{array}} \right.\]

C. \[\left[ {\begin{array}{*{20}{c}}{\overrightarrow b  = (4\sqrt 2 ;2; - 8)}\\{\overrightarrow b  = ( - 4\sqrt 2 ;2;8)}\end{array}} \right.\]

D. \[\left[ {\begin{array}{*{20}{c}}{\overrightarrow b  = (4\sqrt 2 ; - 2;8)}\\{\overrightarrow b  = ( - 4\sqrt 2 ;2; - 8)}\end{array}} \right.\]

Câu 15: Cho \[\overrightarrow a  = (1;m; - 1),\overrightarrow b  = (2;1;3)\].Tı̀m m để \[\overrightarrow a  \bot \overrightarrow b \].

A. m = 1

B. m = −1

C. m = −2

D. m = 2

Câu 16: Cho \[\overrightarrow a  = (1;{\log _3}5;m),\overrightarrow b  = (3;{\log _5}3;4)\]. Tı̀m m để \[\overrightarrow a  \bot \overrightarrow b \].

 A. m = 1

B. m = 2

C. m = −1

D. m = −2

Câu 17: Cho 2 điểm A(2;-1;3); B(4;3;3). Tı̀m điểm M thỏa \[3\overrightarrow {MA}  - 2\overrightarrow {MB}  = \overrightarrow 0 \]

A. M (-2;9;3)

B. M (2;-9;3)

C. M (2;9;-3)

D. M (-2;-9;3)

Câu 18: Trong không gian Oxyz, cho 2 điểm B(1;2;-3) và C(7;4;-2). Nếu E là điểm thỏa mãn đẳng thức \[3\overrightarrow {CE}  = 2\overrightarrow {EB} \] thì tọa độ điểm E là :

A. \[\left( {3;\frac{8}{3};\frac{8}{3}} \right)\]

B. \[\left( {\frac{8}{3};3; - \frac{8}{3}} \right)\]

C. \[\left( {3;3; - \frac{8}{3}} \right)\]

D. \[\left( {1;2;\frac{1}{3}} \right)\]

Câu 19: Trong không gian Oxyz cho 3 điểm A(2;-1;1), B(5;5;4) và C(3;2;-1). Tọa độ tâm G của tam giác ABC là

A. \[\left( {\frac{{10}}{3};\frac{4}{3};2} \right)\]

B. \[\left( {\frac{{10}}{3};2;\frac{4}{3}} \right)\]

C. \[\left( {\frac{1}{3};\frac{4}{3};\frac{{10}}{3}} \right)\]

D. \[\left( {\frac{1}{3};2;\frac{4}{3}} \right)\]

Câu 20: Trong không gian Oxyz, cho 3 điểm A (1;2;0); B (1;0;-1); C(0;-1;2).

A.Tam giác cân đỉnh C.

B. Tam giác vuông đỉnh A.

C. Tam giác đều.

D. Không phải ∆ABC

Câu 21: Trong không gian Oxyz, cho 3 điểm A(5;3;-1); B(2;3;-4); C(1;2;0). Tam giác ABC là:

A.Tam giác cân đỉnh A.

B. Tam giác vuông đỉnh A.

C. Tam giác đều.

D. Không phải ∆ABC.

Câu 22: Trong không gian Oxyz, cho 3 điểm A(1;2;1); B(5;3;4); C(8;-3;2). Tam giác ABC là:

A.Tam giác cân đỉnh A.

B. Tam giác vuông đỉnh B.

C. Tam giác đều.

D. Không phải ∆ABC

Câu 23: ∆ ABC có A(1;0;1); C(0;2;3); D(2;1;0). Độ dài đường cao kẻ từ C là:

A. \[\sqrt {26} \]

B. \[\frac{{\sqrt {26} }}{2}\]

C. \[\frac{{\sqrt {26} }}{3}\]

D. 26

Câu 24: ∆ ABC với A(1;2;0); C(1;0;-1); C(0;-1;2). Diện tích ∆ ABC:

A. \[\frac{{3\sqrt 6 }}{2}\]

B. \[\frac{{6\sqrt 6 }}{3}\]

C. \[\frac{{6\sqrt 3 }}{2}\]

D. \[\frac{3}{2}\]

Câu 25: Cho 3 điểm M(2;0;0); C(0;-3;0); C(0;0;4). Nếu MNPQ là hình bình hành thì tọa độ điểm Q là:

A. Q(2;3;4)

B.Q(-2;-3;-4)

C. Q(-2;-3;4)

D. Q(3;4;2)

Câu 26: Cho vectơ \[\overrightarrow a  = ( - 1;1;0);\overrightarrow b  = (1;1;0)\]. Hình bình hành OADB có\[\overrightarrow {OA}  = \overrightarrow a ,\overrightarrow {OB}  = \overrightarrow b \]. Tọa độ tâm hình bình hành OADB là:

A. (0;1;0)

B.(1;0;0)

C. (1;0;1)

D. (1;0;0)

Câu 27: Ba đỉnh của một hình bình hành có tọa độ (1;1;1); (2;3;4); (6;5;2). Diện tích hình bình hành đó bằng:

A. \[2\sqrt {83} \]

B. \[\sqrt {83} \]

C. 83

D. \[\frac{{\sqrt {83} }}{2}\]

Câu 28: Cho 3 điểm A(3;-1;2); B(1;2;-1); C(-1;1;-3). Nếu ABCD là hình thang thì tọa độ điểm D là:

A. D(2;3;4)

B. D(3;-5;3)

C. D(3;5;3)

D. D(3;5;-3)

Câu 29: Cho 3 vectơ \[\overrightarrow u  = (2; - 1;1);\overrightarrow v  = (m;3; - 1);\overrightarrow w  = (1;2;1)\]. Tìm m để 3 vectơ \[\overrightarrow u ,\overrightarrow v ,\overrightarrow w \] đồng phẳng

A. m = \[\frac{8}{2}\]

B. m = -\[\frac{8}{2}\]

C. m = 8

D. m = - 2

Câu 30: Cho 3 vectơ \[\overrightarrow a  = (1;2;3);\overrightarrow b  = (2;1;m);\overrightarrow c  = (2;m;1)\]. Tìm m để 3 vectơ \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \]không đồng phẳng

A. m ≠ 1 và m ≠ 9

B. m ≠ −1 và m ≠ 9

C. m ≠ 1 và m ≠ −9

D. m ≠ −1 và m ≠ −9

Câu 31: Trong kg Oxyz cho bốn điểm A(1;0;0), B(0;1;0), C(0;0;1), D(1;1;1).Trong các mệnh đề sau, mệnh đề nào sai?

A. Bốn điểm A,B,C,D tạo thành một tứ diện

B. Tam giác ABD là tam giác đều

C. AB ⊥ CD.

D. Tam giác BCD là tam giác vuông

Câu 32: Cho bốn điểm A(1; 1; 0), B(0; 2; 1), C(1; 0; 2), D(1; 1; 1). Tính thể tích khối tứ diện ABCD.

A. \[\frac{1}{6}\]

B. \[\frac{1}{3}\]

C. \[\frac{1}{2}\]

D. 1

Câu 33: Cho bốn điểm A(−2;6;3), B(1;0;6), C(0;2;−1), D(1;4;0). Tính chiều cao AH của tứ diện ABCD:

A. \[\frac{{\sqrt {77} }}{{36}}\]

B. \[\frac{{36}}{{\sqrt {77} }}\]

C. \[\frac{6}{{\sqrt 7 }}\]

D. 5

Câu 34: Tứ diên ABCD có A(2;1;−1), B(3;0;1), C(2;-1;3), điểm D thuộc trục Oy; biết V_ABCD = 5. Tı̀m toa độ điểm D.

A. D (0; −7;0) và B (0;8;0)

B. D (0;7;0) và B (0;8;0)

C. D (0; −7;0) và B (0; −8;0)

D. D (0;7;0) và B (0; −8;0)

Câu 35: Cho B(−1;1;2), A(0;1;1), C(1;0;4). Phát biểu nào sau đây đúng nhất:

A. ∆ ABC vuông tại A

B. ∆ ABC vuông tại B

C. ∆ ABC vuông tại C

D. A, B, C thẳng hàng

Câu 36: Cho 4 điểm: A(7;4;3), B(1;1;1), C(2;–1;2), D(–1;3;1). Phát biểu nào sau đây đúng nhất:

A. 4 điểm A, B, C, D đồng phẳng

B. 4 điểm A, B, C, D không đồng phẳng

C. BC = \[\sqrt 6 \]

D. Đáp án B và C đều đúng

Câu 37: Trong không gian Oxyz cho 3 điểm A(1;0;1), B(-2;1;3) và C(1;4;0). Tọa độ trực tâm H của tam giác ABC là

A. \[\left( {\frac{8}{{13}};\frac{{ - 7}}{{13}};\frac{{15}}{{13}}} \right)\]

B. \[\left( {\frac{8}{{13}};\frac{7}{{13}};\frac{{15}}{{13}}} \right)\]

C. \[\left( {\frac{{ - 8}}{{13}};\frac{{ - 7}}{{13}};\frac{{15}}{{13}}} \right)\]

D. \[\left( {\frac{8}{{13}};\frac{{ - 7}}{{13}};\frac{{ - 15}}{{13}}} \right)\]

Câu 38: Cho 3 điểm A(−1;0;1), B(1;2;−1), C(−1;2;3). Tìm tọa độ trọng tâm G, trực tâm H, tâm I đường tròn ngoại tiếp tam giác ABC

A. \[G\left( { - \frac{1}{3};\frac{4}{3};1} \right);H( - 1;0;1);I(0;2;1)\]

B. \[G\left( {\frac{1}{3};\frac{4}{3};1} \right);H( - 1;0;1);I(0;2;1)\]

C. \[G\left( { - \frac{1}{3};\frac{4}{3};1} \right);H(1;0;1);I(0;2;1)\]

D. \[G\left( { - \frac{1}{3};\frac{4}{3};1} \right);H( - 1;0;1);I(2;0;1)\]

Câu 39: Cho 2 điểm A(1;2;1), B(2;−1;2). Trực tâm H của tam giác OAB có tọa độ:

A. \[H\left( {\frac{3}{5};\frac{3}{5};\frac{3}{5}} \right)\]

B. \[H\left( {\frac{3}{5};\frac{3}{5};\frac{2}{5}} \right)\]

C. \[H\left( {\frac{3}{5};\frac{2}{5};\frac{3}{5}} \right)\]

D. \[H\left( { - \frac{3}{5};\frac{2}{5}; - \frac{3}{5}} \right)\]

Câu 40: Cho 2 điểm A(1;2;1), B(2;−1;2). Tâm I của đường tròn ngoại tiếp tam giác OAB có tọa độ:

A. \[I\left( {\frac{6}{5};\frac{3}{{10}};\frac{6}{5}} \right)\]

B. \[I\left( {\frac{6}{5};\frac{3}{5};\frac{6}{5}} \right)\]

C. \[I\left( {\frac{2}{5};\frac{3}{{10}};\frac{2}{5}} \right)\]

D. \[I\left( {\frac{1}{{10}};\frac{3}{{10}};\frac{1}{{10}}} \right)\]

Câu 41: Cho A(1;−1;1); B(−3;−2;2). Tı̀m tọa độ điểm C trên trục Ox biết AC ⊥ BC

A. C (0;0;–1)

B. C (0;−1;0)

C. C (1;0;0)

D. C (−1;0;0)

Câu 42: Cho A(1;2;−2). Tı̀m điểm B trên trục Oy, biết AB = \[\sqrt 6 \]

A. B (1;1;0) và B (0;3;0)

A. B (0;1;0) và B (3;0;0)

C. B (0;1;0) và B (0;3;0)

D. B (0;0;1) và B (0;3;0)

Câu 43: Cho A(3;1;0); B(−2;4;1). Tìm tọa độ điểm M trên trục Oz cách đều 2 điểm A và B.

A. M (0;0;2)

B. \[M\left( {0;0;\frac{{11}}{2}} \right)\]

C. M (0;0;11)

D. \[M\left( {\frac{{11}}{2};0;0} \right)\]

Câu 44: Hình chiếu H của điểm A(−2;4;3) trên mặt phẳng (P) : 2x – 3y + 6z + 19 = 0 có tọa độ:

A. H (1; –1;2)

B. \[H\left( { - \frac{{20}}{7};\frac{{37}}{7};\frac{3}{7}} \right)\]

C. \[H\left( { - \frac{2}{5};\frac{{37}}{5};\frac{{31}}{5}} \right)\]

D. H (−20;2;3)

Câu 45: Hình chiếu của gốc tọa độ O (0;0;0) trên mặt phẳng (P): x – 2y + z – 1 = 0 có tọa độ:

A. \[H\left( {\frac{1}{6}; - \frac{1}{3};\frac{1}{6}} \right)\]

B. \[H\left( {\frac{1}{6};1; - \frac{1}{6}} \right)\]

C. \[H\left( {1;\frac{1}{6}; - \frac{1}{6}} \right)\]

D. H (0;0;0)

Câu 46: Điểm đối xứng của gốc tọa độ O(0;0;0) qua mặt phẳng (P): x – 2y + z -1 = 0 có tọa độ:

A. (0;0;0)

B. \[H\left( {\frac{1}{3}; - \frac{1}{3}; - \frac{1}{3}} \right)\]

C. \[H\left( {\frac{1}{3}; - \frac{2}{3};\frac{1}{3}} \right)\]

D. \[H\left( { - \frac{1}{3};\frac{2}{3}; - \frac{1}{3}} \right)\]

Câu 47: Cho mp (P) : x – 2y – 3z + 14 = 0 và điểm M (1;−1;1). Tìm tọa độ điểm M’ đối xứng với M qua mp (P).

A. M (−1;3;7)

B. M (1;–3;7)

C. M (2;–3;−2)

D. M (2;–1;1)

Câu 48: Hình chiếu H của M(1; 2; – 6) lên đường thẳng d: \[\frac{{x - 2}}{2} = \frac{{y - 1}}{{ - 1}} = \frac{{z + 3}}{1}\]có tọa độ là :

A. H(– 2; 0; 4)

B. H(–4; 0; 2)

C. H(0; 2; –4)

D. H(2; 0; 4)

Câu 49: Hình chiếu vuông góc của gốc tọa độ O(0;0;0) trên đường thẳng d: \[\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{z}{1}\] có tọa độ:

A. \[H\left( {0; - \frac{1}{2}; - \frac{1}{2}} \right)\]

B. \[H\left( {\frac{1}{2};0; - \frac{1}{2}} \right)\]

C. H (0;0;0)

D. \[H\left( {0;\frac{1}{2};\frac{1}{2}} \right)\]

Câu 50: Điểm đối xứng của gốc tọa độ O(0;0;0) qua đường thẳng d: \[\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{z}{1}\] có tọa độ:

A. H (0;0;0)

B. H (1;0;−1)

C. H (0; −1;−1)

D. H (1;1;0)

Câu 51: Cho điểm A(4;−1;3) và đường thẳng d: \[\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 3}}{1}\]. Tìm tọa độ điểm M là điểm đối xứng với điểm A qua d.

A. M (2; −5;3)

B. M (−1;0;2)

C. M (0; −1;2)

D. M (2; −3;5)

Đặc biệt:

a/ Hình chiếu của điểm M(x₀;y₀;z₀) trên mặt phẳng tọa độ, trục tọa độ: hình chiếu: thiếu đâu 0 đó

b/ Điểm đối xứng của điểm M(x₀;y₀;z₀) qua mặt phẳng tọa độ, trục tọa độ, gốc tọa độ O.

Điểm đối xứng: Thiếu đâu đối đó