Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Các dạng bài tập vận dụng cao hệ tọa độ trong không gian, tài liệu bao gồm 12 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Các dạng bài tập vận dụng cao hệ tọa độ trong không gian

CHƯƠNG 3: PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN Oxyz

Bài 1: Hệ tọa độ trong không gian

A. Lý thuyết trọng tâm

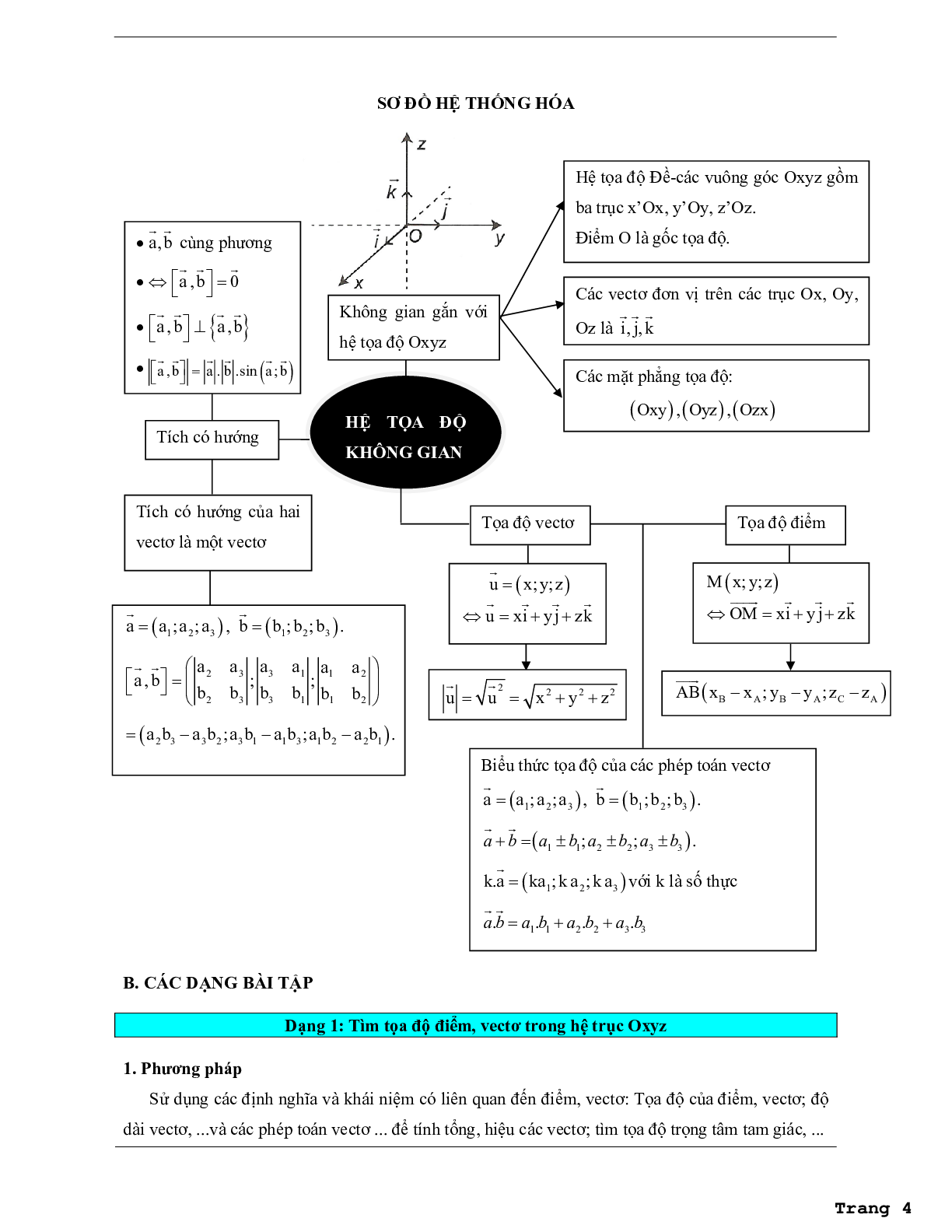
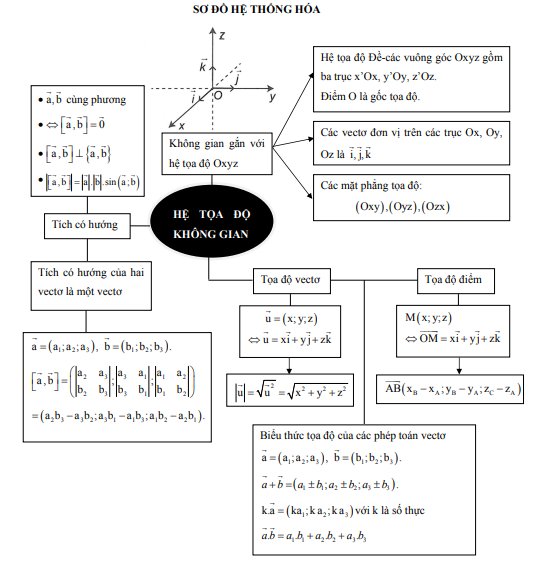
1. Hệ tọa độ trong không gian

Hệ trục tọa độ Đề-các vuông góc trong không gian gồm ba trục x'Ox, y'Oy, z'Oz vuông góc với nhau từng đôi một.

Gọi \[\overrightarrow i ,\overrightarrow j ,\overrightarrow k \] lần lượt là các vectơ đơn vị trên các trục Ox, Oy, Oz.

Điểm O được gọi là gốc tọa độ.

Các mặt phẳng (Oxy), (Oyz), (Ozx) là các mặt phẳng tọa độ.

Không gian gắn với hệ tọa độ Oxyz được gọi là không gian Oxyz.

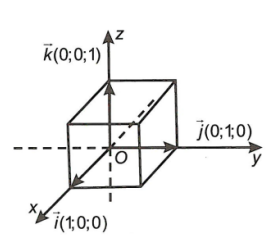
2. Tọa độ của vectơ

Trong không gian Oxyz, cho vectơ u r . Khi đó

\[\overrightarrow u  = (x;y;z) \Leftrightarrow \overrightarrow u  = x\overrightarrow i  + y\overrightarrow j  + z\overrightarrow k \]

Chú ý:

1) \[\overrightarrow 0  = (0;0;0)\]

2) \[\overrightarrow a  = \overrightarrow b  \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{a_1} = {b_1}}\\{{a_2} = {b_2}}\\{{a_3} = {b_3}}\end{array}} \right.\]

3) \[\overrightarrow a \]cùng phương \[\overrightarrow b \] (\[\overrightarrow b  \ne \overrightarrow 0 \])  \[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{a_1} = k{b_1}}\\{{a_2} = k{b_2}}\\{{a_3} = k{b_3}}\end{array}} \right.\]

Biểu thức tọa độ của các phép toán vectơ

Cho hai vectơ \[\overrightarrow a  = ({a_1};{a_2};{a_3}),b = ({b_1};{b_2};{b_3})\]và k là số thực tùy ý.

Khi đó ta có:

\[\overrightarrow a  + \overrightarrow b  = ({a_1} + {b_1};{a_2} + {b_2};{a_3} + {b_3})\].

\[\overrightarrow a  - \overrightarrow b  = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\].

\[k\overrightarrow a  = (k{a_1};k{a_2};k{a_3})\].

\[\overrightarrow a .\overrightarrow b  = {a_1}.{b_1} + {a_2}.{b_2} + {a_3}.{b_3}\]

Ứng dụng của tích vô hướng:

\[\overrightarrow a  \bot \overrightarrow b  = \overrightarrow a .\overrightarrow b  = 0 \Leftrightarrow {a_1}.{b_1} + {a_2}.{b_2} + {a_3}.{b_3} = 0\]

\[{\overrightarrow a ^2} = \overrightarrow a .\overrightarrow a  = a_1^2 + a_2^2 + a_3^2\]

\[\left| {\overrightarrow a } \right| = \sqrt {{{\overrightarrow a }^2}}  = \sqrt {a_1^2 + a_2^2 + a_3^2} \]

\[\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{{a_1}.{b_1} + {a_2}.{b_2} + {a_3}.{b_3}}}{{\sqrt {a_1^2 + a_2^2 + a_3^2} .\sqrt {b_1^2 + b_2^2 + b_3^2} }}\]

Với \[\overrightarrow a  \ne \overrightarrow 0 ,\overrightarrow b  \ne \overrightarrow 0 \].

3. Tọa độ của một điểm

Trong không gian Oxyz, cho điểm M tùy ý

Khi đó \[M(x;y;z) \Leftrightarrow \overrightarrow {OM}  = x\overrightarrow i  + y\overrightarrow j  + z\overrightarrow k \]

Chú ý: Trong hệ tọa độ Oxyz , cho điểm \[M(x;y;z)\]ta có các khẳng định sau:

\[M \equiv O \Leftrightarrow M(0;0;0)\]

\[M \in (Oxy) \Leftrightarrow z = 0\], tức là \[M(x;y;0)\].

\[M \in (Oyz) \Leftrightarrow x = 0\], tức là \[M(0;y;z)\].

\[M \in (Oxz) \Leftrightarrow y = 0\], tức là \[M(x;0;z)\].

\[M \in Ox \Leftrightarrow y = z = 0\], tức là \[M(x;0;0)\].

\[M \in Oy \Leftrightarrow x = z = 0\], tức là \[M(0;y;0)\].

\[M \in Oz \Leftrightarrow x = y = 0\], tức là \[M(0;0;z)\].

Tính chất

Nếu \[A({x_A};{y_A};{z_A})\], \[B({x_B};{y_B};{z_B})\]thì

\[\overrightarrow {AB}  = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\]

Khi đó \[AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2} + {{({z_B} - {z_A})}^2}} \]

Tọa độ trung điểm I của đoạn thẳng AB là

\[I = (\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\]

Tọa độ trọng tâm G của tam giác ABC là \[G = (\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\]

Tọa độ trọng tâm G của tứ diện ABCD là \[G = (\frac{{{x_A} + {x_B} + {x_C} + {x_D}}}{4};\frac{{{y_A} + {y_B} + {y_C} + {y_D}}}{4};\frac{{{z_A} + {z_B} + {z_C} + {z_D}}}{4})\]

4. Tích có hướng của hai vectơ

Định nghĩa

Trong không gian Oxyz, cho hai vectơ \[\overrightarrow a  = ({a_1};{a_2};{a_3}),\overrightarrow b  = ({b_1};{b_2};{b_3})\]. Tích có hướng của hai vectơ \[\overrightarrow a \]và \[\overrightarrow b \] là một vectơ vuông góc với cả hai vectơ \[\overrightarrow a \]và \[\overrightarrow b \], kí hiệu là \[\left[ {\overrightarrow a ,\overrightarrow b } \right]\]và được xác định như sau:

\[\begin{array}{l}\left[ {\overrightarrow a ,\overrightarrow b } \right] = \left( {\left| {\begin{array}{*{20}{c}}{{a_2}}&{{a_3}}\\{{b_2}}&{{b_3}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{{a_3}}&{{a_1}}\\{{b_3}}&{{b_1}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{{a_1}}&{{a_2}}\\{{b_1}}&{{b_2}}\end{array}} \right|} \right)\\ = ({a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1})\end{array}\]

Tính chất

\[\overrightarrow a \]cùng phương với \[\overrightarrow b \]\[ \Leftrightarrow \left[ {\overrightarrow a ,\overrightarrow b } \right] = \overrightarrow 0 \].

\[\left[ {\overrightarrow a ,\overrightarrow b } \right]\]vuông góc với cả hai vecto \[\overrightarrow a \]và \[\overrightarrow b \].

\[\left[ {\overrightarrow b ,\overrightarrow a } \right] =  - \left[ {\overrightarrow a ,\overrightarrow b } \right]\].

\[\left| {\left[ {\overrightarrow a ,\overrightarrow b } \right]} \right| = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\sin (\overrightarrow a ,\overrightarrow b )\].

5. Phương trình mặt cầu

Trong không gian Oxyz, mặt cầu tâm I (a;b;c), bán kính R có phương trình (S): \[{(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\].

Ngược lại phương trình \[{x^2} + {y^2} + {z^2} + 2Ax + 2By + 2Cz + D = 0\]   (1)

Với \[{A^2} + {B^2} + {C^2} - D > 0\]là phương trình mặt cầu tâm I (-A;-B;-C) có bán kính\[R = \sqrt {{A^2} + {B^2} + {C^2} - D} \]

Chú ý: Điều kiện để phương trình (1) là phương trình mặt cầu là:

 \[{A^2} + {B^2} + {C^2} - D > 0\]

B. Các dạng bài tập

Dạng 1: Tìm tọa độ điểm, vectơ trong hệ trục Oxyz

1. Phương pháp

Sử dụng các định nghĩa và khái niệm có liên quan đến điểm, vectơ: Tọa độ của điểm, vectơ; độ dài vectơ, ...và các phép toán vectơ ... để tính tổng, hiệu các vectơ; tìm tọa độ trọng tâm tam giác, ...

2. Bài tập

Bài tập 1. Trong không gian Oxyz, cho \[\overrightarrow a  = ( - 2;2;0),\overrightarrow b  = (2;2;0);\overrightarrow c  = (2;2;2)\]. Giá trị của \[\left| {\overrightarrow a  + \overrightarrow b  + \overrightarrow c } \right|\] bằng

A. 6.

B. \[2\sqrt 6 \].

C. 11.

D. \[2\sqrt {11} \].

Hướng dẫn giải

Chọn D.

Ta có \[\overrightarrow a  + \overrightarrow b  + \overrightarrow c  = (2;6;2)\]nên \[\left| {\overrightarrow a  + \overrightarrow b  + \overrightarrow c } \right| = \sqrt {{2^2} + {6^2} + {2^2}}  = \sqrt {44}  = 2\sqrt {11} \]

Bài tập 2. Trong không gian Oxyz cho hai điểm A(1;2;3), B(1-;0;1). Trọng tâm G của tam giác OAB có tọa độ là:

A. (0;1;1)

B. \[\left( {0;\frac{2}{3};\frac{4}{3}} \right)\]

C. (0;2;4)

D. (-2;-2;-2)

Hướng dẫn giải

Tọa độ trọng tâm tam giác là:

 \[\left\{ {\begin{array}{*{20}{c}}{{x_G} = \frac{{1 - 1 + 0}}{3} = 0}\\{{y_G} = \frac{{2 + 0 + 0}}{3} = \frac{2}{3}}\\{{x_G} = \frac{{3 + 1 + 0}}{3} = \frac{4}{3}}\end{array}} \right. \Rightarrow G\left( {0;\frac{2}{3};\frac{4}{3}} \right)\]

Chọn B.

Bài tập 3. Trong không gian Oxyz, cho vectơ \[\overrightarrow a  = (1; - 2;4),\overrightarrow b  = ({x_0};{y_0};{z_0})\]cùng phương với vectơ \[\overrightarrow a \]. Biết vectơ \[\overrightarrow b \] tạo với tia Oy một góc nhọn và \[\left| {\overrightarrow b } \right| = \sqrt {21} \]

Giá trị của tổng \[{x_0} + {y_0} + {z_0}\] bằng

A. - 3.

B. 6.

C. - 6.

D. 3.

Hướng dẫn giải

Chọn A.

Lại có \[\left| {\overrightarrow b } \right| = \sqrt {21} \] suy ra \[\sqrt {{k^2} + 4{k^2} + 16{k^2}}  = \sqrt {21}  \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{k = 1}\\{k =  - 1}\end{array}} \right.\]

Với k = 1 ta có \[\left| {\overrightarrow b } \right| = (1; - 2;4)\], suy ra góc giữa \[\overrightarrow b \] và Oy thỏa mãn

\[\cos (\overrightarrow b ,Oy) = \frac{{\overrightarrow b .\overrightarrow j }}{{\left| {\overrightarrow b } \right|.\left| {\overrightarrow j } \right|}}\]   trong đó \[\overrightarrow b .\overrightarrow j  =  - 2 < 0\]

Suy ra góc tạo bởi \[\overrightarrow b \] và Oy là góc tù. Suy ra k = 1 không thỏa mãn.

Với k = - 1 ta có \[\left| {\overrightarrow b } \right| = ( - 1;2; - 4)\] suy ra góc giữa \[\overrightarrow b \] và Oy thỏa mãn

\[\cos (\overrightarrow b ,Oy) = \frac{{\overrightarrow b .\overrightarrow j }}{{\left| {\overrightarrow b } \right|.\left| {\overrightarrow j } \right|}}\] trong đó \[\overrightarrow b .\overrightarrow j  = 2 > 0\].

Suy ra góc tạo bởi \[\overrightarrow b \] và Oy là góc nhọn.

Vậy k = - 1 thỏa mãn.

Do đó \[\left| {\overrightarrow b } \right| = ( - 1;2; - 4)\]. Suy ra \[{x_0} + {y_0} + {z_0} =  - 1 + 2 - 4 =  - 3\].