Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 50 câu trắc nghiệm sử dụng phương pháp tọa độ giải bài toán hình học không gian, tài liệu bao gồm 67 trang, 50 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

50 câu trắc nghiệm sử dụng phương pháp tọa độ giải bài toán hình học không gian - có đáp án chi tiết

Nội dung gồm có

ĐỀ BÀI

HƯỚNG DẪN GIẢI

DẠNG TOÁN 1: HÌNH CHÓP CÓ CẠNH BÊN HOẶC MỘT MẶT VUÔNG GÓC VỚI ĐÁY.

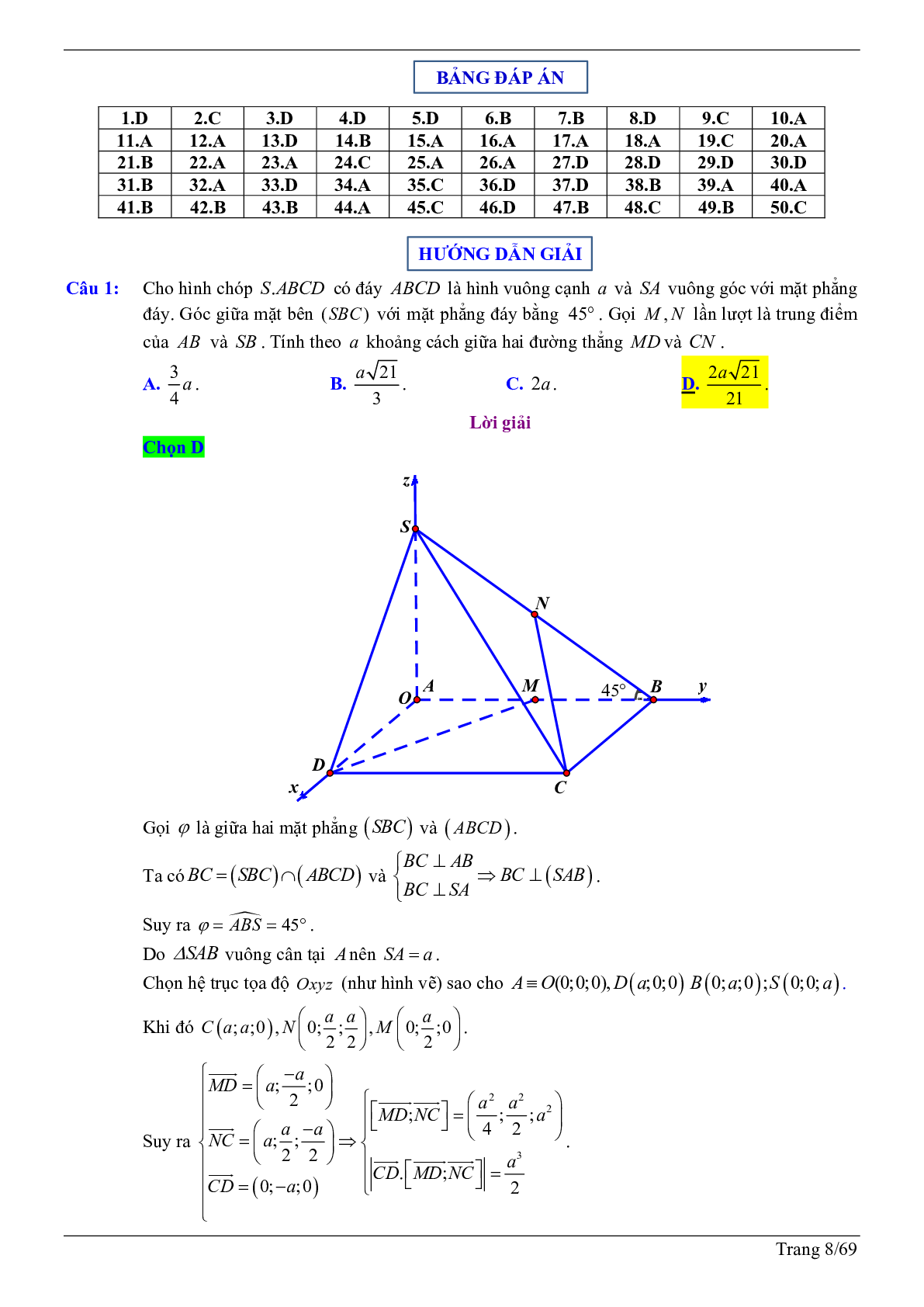
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA vuông góc với mặt phẳng đáy. Góc giữa mặt bên (SBC) với mặt phẳng đáy bằng 45^o . Gọi M N, lần lượt là trung điểm của AB và SB . Tính theo a khoảng cách giữa hai đường thẳng MD và CN .

A. \(\frac{3}{4}a\)

B. \(\frac{{a\sqrt {21} }}{3}\)

C. 2a

D. \(\frac{{2a\sqrt {21} }}{{21}}\)

Câu 2: Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại A, \(\widehat {ABC} = {60^ \circ },BC = 2a\). Gọi D là điểm thỏa mãn\(2\overrightarrow {SB}  = 2\overrightarrow {SD} \). Hình chiếu của S trên mặt phẳng ( ABC) là điểm H thuộc đoạn BC sao cho BC = 4BH. Tính góc giữa hai đường thẳng AD và SC biết SA tạo với mặt đáy một góc 60^o .

A. 60^o

B. 45^o

C. 90^o

D. 30^o

Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 5a , cạnh bên SA = 10a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD . Tính tan của góc tạo bởi hai mặt phẳng ( AMC) và (SBC).

A. \(\frac{{\sqrt 3 }}{2}\)

B. \(\frac{{2\sqrt 3 }}{3}\)

C. \(\frac{{\sqrt 5 }}{5}\)

D. \(\frac{{2\sqrt 5 }}{5}\)

Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SAB đều. Hình chiếu của S lên mặt phẳng ( ABCD) trùng với trung điểm I của AB . Gọi H K, lần lượt là trung điểm của DC và SB , biết\(SH = \frac{{a\sqrt 7 }}{2}\).Tính khoảng cách giữa HK và SC .

A. \(\frac{{\sqrt 3 }}{8}\)

B. \(\frac{{\sqrt {15} }}{2}\)

C. \(\frac{{\sqrt {15} }}{8}\)

D. \(\frac{{\sqrt 5 }}{{10}}\)

Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy, AB = a, AD = 2a, SA = 3a. Gọi M, N lần lượt là hình chiếu của A lên SB, SD và P là giao điểm của SC với mặt phẳng ( AMN) . Tính thể tích khối chóp S.AMPN

A. \(\frac{{1869{a^3}}}{{140}}\)

B. \(\frac{{5589{a^3}}}{{1820}}\)

C. \(\frac{{181{a^3}}}{{120}}\)

D. \(\frac{{1863{a^3}}}{{1820}}\)

Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2 , SA vuông góc với mặt phẳng đáy ( ABCD) và SA = 2 . Gọi M , N lần lượt là hai điểm thay đổi trên hai cạnh AB , AD sao cho mặt phẳng (SMC) vuông góc với mặt phẳng (SNC) . Thể tích khối chóp S.AMCN đạt giá trị nhỏ nhất bằng

A. \(\frac{{4\sqrt 3  + 4}}{3}\)

B. \(\frac{{8\sqrt 3  - 8}}{3}\)

C. \(2\sqrt 3  - 2\)

D. \(\frac{{4\sqrt 3  - 4}}{3}\)

Câu 7: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B , AB = BC = a, AD = 2a; cạnh bên SA vuông góc với mặt phẳng đáy và SA = a. Gọi M , N lần lượt là trung điểm của SB , CD . Tính cosin của góc giữa MN và (SAC).

A. \(\frac{2}{{\sqrt 5 }}\)

B. \(\frac{{\sqrt {55} }}{{10}}\)

C. \(\frac{{3\sqrt 5 }}{{10}}\)

D. \(\frac{1}{{\sqrt 5 }}\)

Câu 8: Cho hình chóp S. ABC có \(\Delta \)ABC vuông tại B , AB = 1, BC =\(\sqrt 3 \), \(\Delta \)SAC đều, mặt phẳng (SAC) vuông với đáy. Gọi \(\alpha \) là góc giữa hai mặt phẳng (SAB) và (SBC). Giá trị của \[cos\alpha \]bằng

A. \(\frac{{2\sqrt {65} }}{{65}}\)

B. \(\frac{{\sqrt {65} }}{{20}}\)

C. \(\frac{{\sqrt {65} }}{{10}}\)

D. \(\frac{{\sqrt {65} }}{{65}}\)

Câu 9: Cho hình lập phương ABCD. A’B’C’D’ có các cạnh bằng 2 , gọi điểm M là tâm của mặt bên ABB’A’ , các điểm N, P, Q, K lần lượt là trung điểm của các cạnh AC, DD’, D’C’, B’C’. Tính cosine góc giữa hai mặt phẳng (MNP) và ( AQK ).

A.\(\frac{{\sqrt 2 }}{2}\)

B. \(\frac{1}{2}\)

C. \(\frac{{\sqrt {102} }}{{34}}\)

D. \(\frac{{\sqrt 3 }}{4}\)

 Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a . SA vuông góc với mặt phẳng đáy. H và K là hai điểm lần lượt nằm trên hai cạnh BC và CD sao cho\(BH = \frac{{3a}}{4},KD = x\left( {0 < x < a} \right)\). Tìm giá trị của x để hai mặt phẳng (SAH) và (SAK) tạo với nhau một góc bằng 45° .

A. \(x = \frac{a}{7}\)

B. \(x = \frac{a}{5}\)

C. \(x = \frac{{2a}}{7}\)

D. \(x = \frac{{2a}}{5}\)

Câu 11: Trong không gian, cho tam giác OAB cân ở O có OA = OB = 5 , \(\tan \widehat {AOB} = \frac{4}{3}\). Điểm C di động trên tia Oz vuông góc (OAB), gọi H là trực tâm của tam giác ABC . Khi C di động trên tia Oz thì H luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng:

A. \(\frac{{\sqrt 5 }}{4}\)

B. \(\frac{{\sqrt 3 }}{2}\)

C. \(\frac{{\sqrt 5 }}{2}\)

D. \(\sqrt 3 \)

Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a, góc \(\widehat {BCD} = {120^o},SA \bot \left( {ABCD} \right)\)Thể tích khối chóp S.ABCD là\(\frac{{{a^3}\sqrt 3 }}{3}\). Gọi M là tâm đường tròn ngoại tiếp tam giác SOD . Hãy tính khoảng cách h từ M tới mặt phẳng (SBC) theo a.

A. \(h = \frac{{a\sqrt {57} }}{{19}}\)

B. \(h = \frac{{a\sqrt {57} }}{{38}}\)

C. \(h = \frac{{2\sqrt 5 a}}{5}\)

D. \(h = \frac{{2\sqrt 5 a}}{{19}}\)

Câu 13: Cho tam giác ABC vuông tại A và đường thẳng \[\Delta \] vuông góc với mặt phẳng ( ABC) tại điểm A . Các điểm M, N thay đổi trên đường thẳng \[\Delta \] sao cho (MBC) \( \bot \) (NBC). Biết AB = b, AC = c. Giá trị nhỏ nhất của thể tích tứ diện MNBC theo b và c bằng

A. \(\frac{{3{b^2}{c^2}}}{{\sqrt {{b^2} + {c^2}} }}\)

B. \(\frac{{{b^2}{c^2}}}{{\sqrt {{b^2} + {c^2}} }}\)

C. \(\frac{{b{c^2}}}{{3\sqrt {{b^2} + {c^2}} }}\)

D. \(\frac{{{b^2}{c^2}}}{{3\sqrt {{b^2} + {c^2}} }}\)

DẠNG TOÁN 2: HÌNH CHÓP ĐỀU VÀ HÌNH CHÓP DẠNG KHÁC.

Câu 14: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O . Gọi M và N lần lượt là trung điểm của hai cạnh SA và BC . Biết 6 2 a MN = \(\frac{{a\sqrt 6 }}{2}\), tính sin của góc giữa đường thẳng MN và mặt phẳng (SBD).

A. \(\frac{{\sqrt 2 }}{5}\)

B. \(\frac{{\sqrt 3 }}{3}\)

C. \(\frac{{\sqrt 5 }}{5}\)

D. \(\sqrt 3 \)

Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Gọi M và N lần lượt là trung điểm các cạnh AB và AD; H là giao điểm của CN và DM . Biết SH vuông góc với mặt phẳng (ABCD) và\(SH = a\sqrt 3 \). Tính khoảng cách giữa hai đường thẳng DM và SC theo a .

A. \(\frac{{2a\sqrt {57} }}{{19}}\)

B. \(\frac{{a\sqrt {57} }}{{19}}\)

C. \(\frac{{2a\sqrt {13} }}{{19}}\)

D. \(\frac{{a\sqrt 7 }}{{19}}\)

Câu 16: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng nhau. Gọi E M, lần lượt là trung điểm các cạnh BC, SA, a là góc tạo bởi đường thẳng EM và mặt phẳng (SBD). Tính sin\(\alpha \) .

A. \(\sin \alpha  = \frac{{\sqrt 6 }}{3}\)

B. \(\sin \alpha  = \frac{1}{2}\)

C. \(\sin \alpha  = \frac{{\sqrt 3 }}{2}\)

D. \(\sin \alpha  = \frac{{\sqrt 2 }}{2}\)

Câu 17: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng h. Gọi I là trung điểm cạnh bên SC . Tính khoảng cách từ S đến mặt phẳng ( AIB) .

A. \(\frac{{2ah}}{{\sqrt {4{h^2} + 9{a^2}} }}\)

B. \(\frac{{4ah}}{{\sqrt {4{h^2} + 9{a^2}} }}\)

C. \(\frac{{ah}}{{\sqrt {4{h^2} + 9{a^2}} }}\)

D. \(\frac{{2ah}}{{\sqrt {2{h^2} + 3{a^2}} }}\)

Câu 18: Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a , tâm O . Gọi E là điểm đối xứng với D qua trung điểm của SA, M là trung điểm của AE , N là trung điểm của BC . Tính khoảng cách giữa hai đường thẳng MN và AC .

A. \(\frac{{a\sqrt 2 }}{4}\)

B. \(\frac{{a\sqrt 2 }}{2}\)

C. \(\frac{{a\sqrt 3 }}{4}\)

D. \(\frac{a}{8}\)

Câu 19: Cho hình lăng trụ ABC.A’B’C’ có A’.ABC là tứ diện đều cạnh a . Gọi M , N lần lượt là trung điểm của AA’ và BB’. Tính tan của góc giữa hai mặt phẳng ( ABC) và (CMN) .

A. \(\frac{{\sqrt 2 }}{5}\)

B. \(\frac{{3\sqrt 2 }}{4}\)

C. \(\frac{{2\sqrt 2 }}{5}\)

D. \(\frac{{4\sqrt 2 }}{{13}}\)

Câu 20: Cho hình chóp SABC có đáy ABC là tam giác cân tại A và AB = a,\(\widehat {BAC} = {120^o}\). SA = SB = SC. Gọi \(\alpha \) là góc của hai mặt phẳng (SAB) và (SBC) sao cho\(\cos \alpha  = \frac{5}{7}\). Khi đó thể tích của khối chóp SABC là

A. \(\frac{{\sqrt 3 {a^3}}}{{12}}\)

B. \(2{a^3}\)

C. \(\frac{{{a^3}}}{3}\)

D. \(\frac{{2{a^3}}}{{\sqrt 5 }}\)

Câu 21: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AC = 2a , tam giác SAB và tam giác SCB lần lượt vuông tại A , C . Khoảng cách từ S đến mặt phẳng ( ABC) bằng 2a . Côsin của góc giữa hai mặt phẳng (SAB) và (SCB) bằng:

A. \(\frac{1}{2}\)

B. \(\frac{1}{3}\)

C. \(\frac{1}{{\sqrt 2 }}\)

D. \(\frac{1}{{\sqrt 3 }}\)

Câu 22: Cho hình chóp đều SABCD có cạnh đáy bằng 2 , cạnh bên bằng \(3\sqrt 2 \). Gọi M N, lần lượt là các điểm thuộc SB, SD sao cho SB =3SM, SD = 3DN. Khoảng cách giữa AM và CN bằng

A. \(\frac{{40}}{{\sqrt {857} }}\)

B. \(\frac{{72}}{{\sqrt {857} }}\)

C. \(\frac{{24}}{{\sqrt {153} }}\)

D. \(\frac{{40}}{{\sqrt {257} }}\)

Câu 23: Cho hình chóp tam giác đều S.ABC có SA = 2a , AB = a. Gọi M là trung điểm cạnh BC . Tính khoảng cách d từ M tới mặt phẳng (SAB).

A. \(d = \frac{{a\sqrt {165} }}{{30}}\)

B. \(d = \frac{{a\sqrt {15} }}{3}\)

C. \(d = \frac{{a\sqrt {65} }}{{15}}\)

D. \(d = \frac{{a\sqrt {65} }}{{10}}\)

Câu 24: Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD = 2AB = 2BC = 2CD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng ( ABCD) . Gọi M, N lần lượt là trung điểm của SB và CD. Tính cosin góc giữa MN và (SAC), biết thể tích khối chóp S.ABCD bằng \(\frac{{{a^3}\sqrt 3 }}{4}\).

A. \(\frac{{\sqrt 5 }}{{10}}\)

B. \(\frac{{3\sqrt {310} }}{{20}}\)

C. \(\frac{{\sqrt {310} }}{{20}}\)

D. \(\frac{{3\sqrt 5 }}{{10}}\)

Câu 25: Cho hình chóp SABC có đáy ABC là tam giác vuông tại A , AB = 3 a, AC = 4a. Các mặt bên (SAB), (SAC), (SBC) cùng tạo với đáy ( ABC) một góc 45⁰  . Biết chân đường vuông góc hạ từ S xuống mặt phẳng ( ABC) nằm ở miền trong tam giác ABC . Gọi góc tạo bởi hai mặt phẳng (SAC) và (SBC) là \(\alpha \) . Tính cos\(\alpha \) .

A. \(\cos \alpha  = \frac{1}{{10}}\)

B. \(\cos \alpha  = \frac{1}{5}\)

C. \(\cos \alpha  = \frac{3}{5}\)

D. \(\cos \alpha  = \frac{1}{{15}}\)

Câu 26: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng ( ABC) là điểm H thuộc cạnh AB sao cho HA = 2HB. Góc giữa đường thẳng SC và mặt phẳng ( ABC) bằng 60^o . Tính khoảng cách h giữa hai đường thẳng SA và BC theo a .

A. \(\frac{{a\sqrt {42} }}{8}\)

B. \(\frac{{a\sqrt {42} }}{{12}}\)

C. \(\frac{{a\sqrt {42} }}{4}\)

D. \(\frac{{a\sqrt {42} }}{{24}}\)

DẠNG TOÁN 3: HÌNH LĂNG TRỤ TAM GIÁC.

Câu 27: Cho hình lăng trụ đứng ABC.A’B’C’ có AB = AC = a, góc\(\widehat {ABC} = {30^o}\), góc giữa đường thẳng A’B và mặt phẳng ( ABC) bằng 45⁰ . Gọi M , N lần lượt là trung điểm của B’C’ và CC’ . Cosin của góc giữa mặt phẳng( AMN) và mặt phẳng ( ABC) bằng

A. \(\frac{1}{2}\)

B. \(\frac{{\sqrt 2 }}{2}\)

C. \(\frac{{\sqrt {13} }}{4}\)

D. \(\frac{{\sqrt 3 }}{4}\)

Câu 28: Cho hình lăng trụ tam giác ABC.A’B’C’ có đáy ABClà tam giác đều cạnh a và các mặt bên đều là các hình vuông cạnh a . Gọi G là trọng tâm của tam giác ABCvà I là trung điểm của đoạn thẳng CC’. Khoảng cách giữa hai đường thẳng A’B và GI bằng

A. \(\frac{{a\sqrt {11} }}{{22}}\)

B. \(\frac{{3a\sqrt {11} }}{7}\)

C. \(\frac{{a\sqrt {11} }}{{12}}\)

D. \(\frac{{3a\sqrt {11} }}{{22}}\)

Câu 29: Cho lăng trụ đứng ABC.A’B’C’có đáy là tam giác ABC vuông cân tại A , cạnh\(BC = a\sqrt 6 \). Góc giữa mặt phẳng ( AB’C) và mặt phẳng (BCC’B’) bằng 60^o . Tính thể tích V của khối lăng trụ ABC.A’B’C’?

A. \(V = \frac{{2{a^3}\sqrt 3 }}{3}\)

B. \(V = \frac{{{a^3}\sqrt 3 }}{2}\)

C. \(V = \frac{{3{a^3}\sqrt 3 }}{4}\)

D. \(V = \frac{{3{a^3}\sqrt 3 }}{2}\)

Câu 30: Cho hình lăng trụ đứng ABC.A’B’C’có đáy ABC là tam giác cân, với AB = AC = a và góc\(\widehat {BAC} = {120^o}\), cạnh bên AA’ = a. Gọi M là trung điểm của CC’ . Cosin của góc tạo bởi hai mặt phẳng ( ABC) và ( AB’M) bằng

A. \(\frac{{\sqrt {11} }}{{11}}\)

B. \(\frac{{\sqrt {33} }}{{11}}\)

C. \(\frac{{\sqrt {10} }}{{10}}\)

D. \(\frac{{\sqrt {30} }}{{10}}\)

Câu 31: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại A , AB = AC = a và có cạnh bên bằng 2a. Gọi M, N lần lượt là trung điểm BB’, CC’. Tính khoảng cách từ điểm A đến mặt phẳng (A’MN)

A. a

B. \(\frac{{2a\sqrt 3 }}{3}\)

C. \(\frac{{3a}}{2}\)

D. \(a\sqrt 3 \)

Câu 32: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân tại C , AB = 2 a , AA’ = a , góc giữa BC’ và ( ABB’A’) bằng 60° . Gọi N là trung điểm AA’ và M là trung điểm BB’ . Tính khoảng cách từ điểm M đến mặt phẳng (BC’N) .

A. \(\frac{{2a\sqrt {74} }}{{37}}\)

B. \(\frac{{a\sqrt {74} }}{{37}}\)

C. \(\frac{{2a\sqrt {37} }}{{37}}\)

D. \(\frac{{a\sqrt {37} }}{{37}}\)

Câu 33: Cho hình lăng trụ đứng ABC.A’B’C’ có AB = AC = a, góc BAC bằng 120° , AA’ = a. Gọi M , N lần lượt là trung điểm B’C’ và CC’ . Khoảng cách giữa 2 đường thẳng MN và AH là

A. \(\frac{{a\sqrt 3 }}{2}\)

B. \(\frac{{a\sqrt 3 }}{4}\)

C. \(\frac{{a\sqrt 6 }}{2}\)

D. \(\frac{{a\sqrt 6 }}{4}\)

Câu 34: Cho hình lăng trụ ABC.A₁B₁C₁ có đáy là tam giác đều cạnh a.AA₁ = 2a và vuông góc với mặt phẳng ( ABC). Gọi D là trung điểm của BB₁ , M di động trên cạnh AA₁ . Giá trị lớn nhất của diện tích \(\Delta M{C_1}D\) là

A. \(\frac{{{a^2}\sqrt {15} }}{4}\)

B. \(\frac{{{a^2}\sqrt {15} }}{6}\)

C. \(\frac{{{a^2}\sqrt 5 }}{4}\)

D. \(\frac{{{a^2}\sqrt {10} }}{4}\)

Câu 35: Cho lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a , M là điểm di chuyển trên đường thẳng A’C’; Tính khoảng cách lớn nhất giữa AM và BC’

A. \(\frac{{a\sqrt {34} }}{6}\)

B. \(\frac{{a\sqrt {17} }}{4}\)

C. \(\frac{{a\sqrt {14} }}{4}\)

D. \(\frac{{a\sqrt {21} }}{6}\)