Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Một số công thức tính bán kính mặt cầu, tài liệu bao gồm 8 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Một số công thức tính bán kính mặt cầu

Một số công thức tính bán kính mặt cầu

Nhận xét 1. Xét hình chóp S.ABC, đường tròn ngoại tiếp tam giác ABC có tâm O và bán kính R_d. Gọi R là bán kính mặt cầu ngoại tiếp hình chóp S.ABC, ta có các trường hợp sau:

(1) Nếu SA \( \bot \) (ABC) thì \(R = \sqrt {\frac{{S{A^2}}}{4} + R_d^2} \)                            (1)

(2) Nếu SA = SB = SC thì \(R = \frac{{S{A^2}}}{{2SO}}\)                                      (2)

(3) Nếu (SAB) \( \bot \) (ABC) và bán kính đường tròn ngoại tiếp \(\Delta \)SAB bằng R_b thì

\(R = \sqrt {d{{\left( {O,AB} \right)}^2} + R_b^2} \)                                                       (3)

Chứng minh. (1) và (2) đơn giản. (3) Gọi I là tâm mặt cầu ngoại tiếp hình chóp S.ABC và K là tâm đường tròn ngoại tiếp tam giác SAB. Ta có IO \( \bot \) (ABC) và IK\( \bot \) (SAB). Xét tam giác IAK, ta có

\(I{A^2} = \sqrt {I{K^2} + A{K^2}}  = \sqrt {d{{\left( {O,AB} \right)}^2} + R_B^2} \)

Để ý rằng OI // (SAB) nên IK = d(O,(SAB)) = d(O, AB).

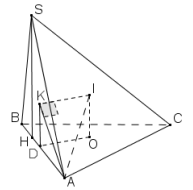
Ví dụ 1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = 2a. Cạnh bên SA vuông góc với mặt đáy và SA =\(a\sqrt 3 \). Tính bán kính của mặt cầu ngoại tiếp hình chóp S.ABC.

Giải. Để áp dụng (1), chỉ cần tính được bán kính đáy R_d. Vì đáy là tam giác vuông tại B nên \({R_d} = \frac{{BC}}{2} = \frac{{a\sqrt 5 }}{2}\). Vậy bán kính cần tìm bằng\(\sqrt {\frac{{S{A^2}}}{4} + R_d^2}  = a\sqrt 2 \).

Ví dụ 2. Cho lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng nhau và bằng 2a. Tính diện tích S của mặt cầu ngoại tiếp hình lăng trụ đã cho

Giải. Mặt cầu đã cho cũng là mặt cầu ngoại tiếp hình chóp A’.ABC, nên với A’A \( \bot \)(ABC) ta có thể áp dụng

\(R = \sqrt {\frac{{A'{A^2}}}{4} + R_d^2}  = \sqrt {{a^2} + {{\left( {\frac{{2a}}{{\sqrt 3 }}} \right)}^2}}  = \frac{{a\sqrt {21} }}{3}\).

Diện tích mặt cầu là\(4\pi {R^2} = \frac{{28\pi {a^2}}}{3}\).

Ví dụ 3. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc. Biết rằng OA = a, OB = b, OC = c, tính bán kính mặt cầu ngoại tiếp tứ diện OABC.

Giải. Ta có AO \( \bot \) (OBC) nên có có thể áp dụng (1),

\(R = \sqrt {\frac{{O{A^2}}}{4} + R_d^2}  = \frac{1}{2}\sqrt {O{A^2} + O{B^2} + O{C^2}} \)

Công thức này cho phép xây dựng một số bài toán thú vị liên quan đến tứ diện vuông. Chẳng hạn

BT 1. Cho tứ diện OABC có A, B, C thay đổi nhưng luôn thỏa mãn OA, OB, OC đôi một vuông góc và 2OA+OB +OC = 3. Giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp OABC là

A. \(\frac{{\sqrt 6 }}{4}\)

B. \(\frac{{\sqrt 2 }}{2}\)

C. \(\frac{{3\sqrt 3 }}{8}\)

D. \(\frac{3}{4}\)

BT 2. Cho ba tia Ox, Oy, Oz đôi một vuông góc với nhau. Gọi C là điểm cố định trên Oz, đặt OC = 1; các điểm AB, thay đổi trên OxOy, sao cho OA + OB = OC. Tìm giá trị bé nhất của bán kính mặt cầu ngoại tiếp tứ diện OABC.

A. \(\frac{{\sqrt 6 }}{3}\)

B. \(\sqrt 6 \)

C. \(\frac{{\sqrt 6 }}{4}\)

D. \(\frac{{\sqrt 6 }}{2}\)

Ví dụ 4. Cho hình chóp tam giác đều S.ABC có đáy ABC là tam giác đều cạnh a, \(SA = \frac{{2a}}{{\sqrt 3 }}\). Gọi D là điểm đối xứng của A qua BC. Tính bán kính của mặt cầu ngoại tiếp hình chóp S.BCD.

Giải. Gọi H là trọng tâm của tam giác ABC, ta có SH \( \bot \) (ABC).

Bán kính đường tròn ngoại tiếp tam giác BCD bằng\(AH = \frac{a}{{\sqrt 3 }}\).

Trong khi ta có DH = 2AH, thế nên H thuộc đường tròn ngoại tiếp tam giác BCD. Vậy có thể áp dụng (1),

\(R = \sqrt {\frac{{S{H^2}}}{4} + R_d^2}  = \frac{{a\sqrt {21} }}{6}\)

Như vậy, có thể ‘nới rộng’ điều kiện áp dụng của (1), đó là khi hình chiếu của đỉnh S

‘rơi’ trên đường tròn ngoại tiếp đáy.

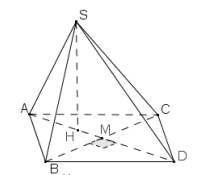
Ví dụ 5. Tính thể tích của khối cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng a.

Giải. Xét hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Vì các hình chóp S.ABCD và S.ABC có cùng mặt cầu ngoại tiếp nên với SA = SB = SC ta có thể áp dụng (2) để có \(R = \frac{{S{A^2}}}{{2SO}}\)

Ta có \(SO = \sqrt {S{A^2} - O{A^2}}  = \sqrt {{a^2} - \frac{{{a^2}}}{2}}  = \frac{a}{{\sqrt 2 }}\)

suy ra\(R = \frac{a}{{\sqrt 2 }}\).

Vậy thể tích khối cầu bằng\(\frac{4}{3}\pi {R^3} = \frac{{\pi {a^3}\sqrt 2 }}{3}\).

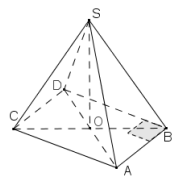
Ví dụ 6. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 1. Hình chiếu của đỉnh S lên mặt đáy trùng với tâm O của đường tròn ngoại tiếp tam giác ABC. Biết rằng bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng \(\frac{2}{3}\) . Tính thể tích khối chóp.

Giải. Vì S cách đều A, B, C nên có thể áp dụng (2). Ta có các liên hệ

\(\left\{ {\begin{array}{*{20}{c}}{S{A^2} = SO + \frac{1}{3}}\\{\frac{{S{A^2}}}{{2SO}} = \frac{2}{3}}\end{array}} \right.\)

Giải hệ này thu được SO = 1, vậy thể tích khối chóp đã cho là\(\frac{{\sqrt 3 }}{{12}}\).

Ví dụ 7. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Đường thẳng BC tạo với (SAC) một góc 30⁰ . Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC.

Giải. Áp dụng (3), ta cần tính bán kính R_b của đường tròn ngoại tiếp \(\Delta \)SAB và d(O, AB) với O là trung điểm của BC. Vì \(\Delta \)SAB đều nên có ngay \({R_b} = \frac{1}{{\sqrt 3 }}\)(cho a = 1).

Gọi H là trung điểm cạnh AB, theo giả thiết ta có SH \( \bot \) (ABC). Dễ có d(B,(SAC)) = 2d(H,(SAC)) = \(\frac{{\sqrt 3 }}{2}\) và d(B; (SAC)) = BC sin 30⁰ ⇒ BC =\(\sqrt 3 \).

Từ đây suy ra AC = \(\sqrt 2 \) và do đó d(O; AB) =\(\frac{{AC}}{2} = \frac{1}{{\sqrt 2 }}\).

Vậy bán kính cần tìm

\(R = \sqrt {R_b^2 + d{{\left( {O,AB} \right)}^2}}  = \sqrt {\frac{5}{6}} \)

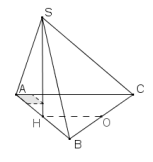
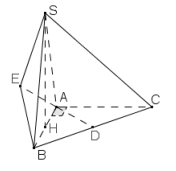
Ví dụ 8. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AC = a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi D là trung điểm của cạnh BC và E là điểm đối xứng của D qua A. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABE.

A. \(\frac{{a\sqrt {21} }}{6}\)

B. \(\frac{a}{{\sqrt 3 }}\)

C. \(\frac{{2a}}{{\sqrt 3 }}\)

D. \(\frac{a}{2}\)

Giải. Gọi H là trung điểm của cạnh AB, vì (SAB)\( \bot \) (ABC) nên ta có SH\( \bot \) (ABC). Đối với hình chóp S.ABE, ta có thể áp dụng (3),

\(R = \sqrt {R_b^2 + d{{\left( {O,\left( {AB} \right)} \right)}^2}} \)

Với O là tâm của đường tròn ngoại tiếp tam giác EAB, tuy nhiên không cần thiết xác định vị trí của O, vì ta có

\(d{\left( {O,AB} \right)^2} = R_d^2 - \frac{{A{B^2}}}{4} = \left( {\frac{{a\sqrt 5 }}{2}} \right) - \frac{a}{4} = a\)

R_b là bán kính đường tròn ngoại tiếp tam giác đều SAB, tức là\({R_b} = \frac{a}{{\sqrt 3 }}\).

Vậy bán kính mặt cầu ngoại tiếp hình chóp S.ABE là\(\frac{{2a}}{{\sqrt 3 }}\).

Như vậy trong tình huống khó xác định được vị trí của tâm O, ta có thể dùng (2) dưới dạng (2’) như sau:

\(R = \sqrt {R_b^2 + R_c^2 - \frac{{A{B^2}}}{4}} \)

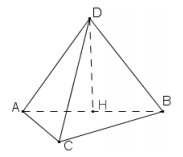
Ví dụ 9. Cho tứ diện ABCD có ABD là tam giác đều cạnh a, CD = a và (ABC)\( \bot \) (ABD). Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD theo a.

A. \(\frac{{a\sqrt 3 }}{6}\)

B. \(\frac{a}{2}\)

C. \(\frac{{2a}}{{\sqrt 3 }}\)

D. \(\frac{a}{{\sqrt 3 }}\)

Giải. Vì (ABC)\( \bot \) (ABD) nên ta có DH\( \bot \) (ABC) với H là trung điểm của cạnh AB. Vì D cách đều A, B, C nên H trùng với tâm O của đường tròn ngoại tiếp tam giác ABC, tức là d(O, AB) = 0. Như vậy trong trường hợp này, (3) trở thành \(R = {R_b} = \frac{a}{{\sqrt 3 }}\).

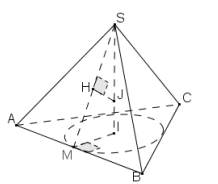
Nhận xét 2. Cho hình chóp S.ABC, đường tròn nội tiếp đáy ABC có tâm I, bán kính rd, SI\( \bot \) (ABC) và SI = h. Khi đó, bán kính r của mặt cầu nội tiếp hình chóp S.ABC thỏa mãn 0 < r < \(\frac{h}{2}\)và đồng thời

\(h{r^2} + 2r_d^2r - r_d^2h = 0\)                         (4)

Chứng minh. Gọi J là tâm mặt cầu nội tiếp hình chóp S.ABC. Kẻ IM\( \bot \)AB tại M thì ta có AB\( \bot \) (SIM). Kẻ tiếp JH\( \bot \)SM tại H, kết hợp với AB\( \bot \)JH ta được JH\( \bot \) (SAB). Vậy JH là bán kính mặt cầu nội tiếp hình chóp S.ABC. Đặt JH = JI = r vì \(\Delta SHI \sim \Delta SIM\)nên \(\frac{{SH}}{{SI}} = \frac{{JH}}{{IM}} \Leftrightarrow \frac{{\sqrt {{{\left( {h - r} \right)}^2} - {r^2}} }}{h} = \frac{r}{{{r_d}}}\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{h{r^2} + 2r_d^2r - r_d^2h = 0}\\{0 < r < \frac{h}{2}}\end{array}} \right.\)

Ví dụ 10. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,\(\widehat {ABC} = {60^0}\). Hình chiếu của S lên mặt đáy trùng với giao điểm O của AC và BD. Cho biết\(SO = \frac{a}{4}\), tính theo a bán kính mặt cầu nội tiếp hình chóp S.ABCD.

A. \(\frac{{\sqrt 3  - 1}}{4}a\)

B. \(\frac{{2 - \sqrt 3 }}{2}a\)

C. \(\frac{{2\sqrt 3  + 3}}{4}a\)

D. \(\frac{{2\sqrt 3  - 3}}{4}a\)

Giải. Vì O chính là tâm đường tròn nội tiếp hình thoi ABCD và SO\( \bot \) (ABCD) nên có thể áp dụng nhận xét 2. Vậy chỉ cần tính thêm r_d, ta có

\({r_d} = d\left( {O,AB} \right) = \frac{{a\sqrt 3 }}{4}\)

Bán kính r của mặt cầu thỏa phương trình

\(h{r^2} + 2r_d^2r - hr_d^2 = 0\)

thử các phương án chọn D.

Ví dụ 11. Cho một mặt cầu có bán kính bằng 1. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên. Hỏi thể tích nhỏ nhất của chúng bằng bao nhiêu

A. \(4\sqrt 3 \)

B. \(8\sqrt 3 \)

C. \(9\sqrt 3 \)

D. \(16\sqrt 3 \)

Giải. Đặt x, h lần lượt là độ dài cạnh đáy và chiều cao của hình chóp tam giác đều ngoại tiếp mặt cầu bán kính 1. Khi đó, bán kính đường tròn nội tiếp đáy là\(\frac{{x\sqrt 3 }}{6}\). Ta có theo (4),

\(h{.1^2} + 2{\left( {\frac{{x\sqrt 3 }}{6}} \right)^2}.1 - {\left( {\frac{{x\sqrt 3 }}{6}} \right)^2}h = 0 \Rightarrow h = \frac{{2{x^2}}}{{{x^2} - 12}}\)

Thể tích khối chóp \(V = \frac{1}{3}.\frac{{{x^2}\sqrt 3 }}{4}.\frac{{2{x^2}}}{{{x^2} - 12}}\)

Khảo sát hàm số trên \(\left( {\sqrt {12} ; + \infty } \right)\)  cho thấy\(V \ge 8\sqrt 3 \). Chọn B