Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết và bài tập về mặt tròn xoay - mặt nón trụ cầu, tài liệu bao gồm 64 trang gồm có lý thuyết, bài tập và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Lý thuyết và bài tập về mặt tròn xoay - mặt nón trụ cầu - có đáp án chi tiết

MỤC LỤC

HÌNH NÓN - KHỐI NÓN

A -LÝ THUYẾT TÓM TẮT

B – BÀI TẬP

HÌNH TRỤ - KHỐI TRỤ

A – LÝ THUYẾT TÓM TẮT

B – BÀI TẬP

MẶT CẦU – KHỐI CẦU

A – LÝ THUYẾT TÓM TẮT

B – BÀI TẬP

HÌNH NÓN - KHỐI NÓN

A – LÝ THUYẾT TÓM TẮT

1) Mặt nón tròn xoay

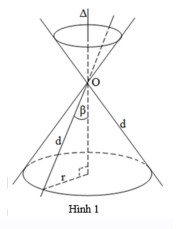
+ Trong mặt phẳng (P), cho 2 đường thẳng d, \(\Delta \) cắt nhau tại O và chúng tạo thành góc \(\beta \) với\(0 < \beta  < {90^0}\). Khi quay mp(P) xung quanh trục \(\Delta \) với góc \(\beta \) không thay đổi được gọi là mặt nón tròn xoay đỉnh O (hình 1).

+ Người ta thường gọi tắt mặt nón tròn xoay là mặt nón. Đường thẳng \(\Delta \) gọi là trục, đường thẳng d được gọi là đường sinh và góc 2\(\beta \) gọi là góc ở đỉnh.

2) Hình nón tròn xoay

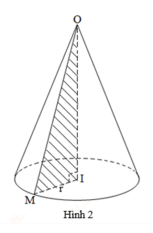
+ Cho \(\Delta \)OIM vuông tại I quay quanh cạnh góc vuông OI thì đường gấp khúc OIM tạo thành một hình, gọi là hình nón tròn xoay (gọi tắt là hình nón) (hình 2).

+ Đường thẳng OI gọi là trục, O là đỉnh, OI gọi là đường cao và OM gọi là đường sinh của hình nón.

+ Hình tròn tâm I, bán kính r = IM là đáy của hình nón.

3) Công thức diện tích và thể tích của hình nón

Cho hình nón có chiều cao là h, bán kính đáy r và đường sinh là l thì có:

+ Diện tích xung quanh: \({S_{xq}} = \pi .r.l\)

+ Diện tích đáy (hình tròn): \({S_{tr}} = \pi .{r^2}\)

+ Diện tích toàn phần hình tròn: S = Str + Sxq

+ Thể tích khối nón: Vnón =\(\frac{1}{3}Str.h = \frac{1}{3}\pi .{r^2}.h\).

4) Tính chất:

Nếu cắt mặt nón tròn xoay bởi mặt phẳng đi qua đỉnh thì có các trường hợp sau xảy ra:

+ Mặt phẳng cắt mặt nón theo 2 đường sinh =>Thiết diện là tam giác cân.

+ Mặt phẳng tiếp xúc với mặt nón theo một đường sinh. Trong trường hợp này, người ta gọi đó là mặt phẳng tiếp diện của mặt nón.

Nếu cắt mặt nón tròn xoay bởi mặt phẳng không đi qua đỉnh thì có các trường hợp sau xảy ra:

+ Nếu mặt phẳng cắt vuông góc với trục hình nón =>giao tuyến là một đường tròn.

+ Nếu mặt phẳng cắt song song với 2 đường sinh hình nón =>giao tuyến là 2 nhánh của 1 hypebol.

+ Nếu mặt phẳng cắt song song với 1 đường sinh hình nón =>giao tuyến là 1 đường parabol.

B – BÀI TẬP

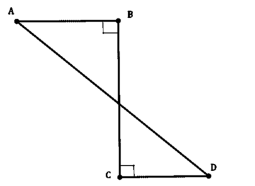
Câu 1: Hình ABCD khi quay quanh BC thì tạo ra:

 A. Một hình trụ

B. Một hình nón

C. Một hình nón cụt

D. Hai hình nón

Hướng dẫn giải: Gọi O là giao điểm của BC và AD. Khi quay hình ABCD quanh BC tức là tam giác vuông OBA quanh OB và tam giác vuông OCD quanh OC. Mỗi hình quay sẽ tạo ra một hình nón nên hình tạo ra sẽ tạo ra 2 hình nón.

Chọn đáp án D.

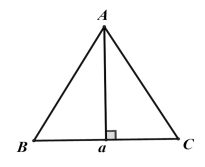
Câu 2: Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Diện tích xung quanh của hình nón đó là :

A. \(\pi {a^2}\)

B. \(2\pi {a^2}\)

C. \(\frac{1}{2}\pi {a^2}\)

D. \(\frac{3}{4}\pi {a^2}\)

Hướng dẫn giải:

\(r = \frac{a}{2};l = a;{S_{xq}} = \pi rl = \frac{{\pi {a^2}}}{2}\)

Chọn đáp án C.

Câu 3: Một hình nón có đường cao h = 20 cm , bán kính đáy r = 25 cm . Tính diện tích xung quanh của hình nón đó:

A. \(5\pi \sqrt {41} \)

B. \(25\pi \sqrt {41} \)

C. \(75\pi \sqrt {41} \)

D. \(125\pi \sqrt {41} \)

Hướng dẫn giải:

Đường sinh của hình nón: \(l = \sqrt {{h^2} + {r^2}}  = 5\sqrt {41} cm\)

Diện tích xung quanh: \({S_{xq}} = \pi rl = 125\pi \sqrt {41} c{m^2}\)

Chọn đáp án D.

Câu 4: Cắt khối nón bởi một mặt phẳng qua trục tạo thành một tam giác ABC đều có cạnh bằng a, biết B, C thuộc đường tròn đáy. Thể tích của khối nón là:

A. \({a^3}\pi \sqrt 3 \)

B. \(\frac{{2\sqrt 3 \pi {a^3}}}{9}\)

C. \(\frac{{{a^3}\pi \sqrt 3 }}{{24}}\)

D. \(\frac{{3{a^3}\pi }}{8}\)

Hướng dẫn giải:

Bán kính đáy khối nón là \(\frac{a}{2}\), chiều cao khối nón là\(\frac{{a\sqrt 3 }}{2}\), suy ra

\(V = \frac{1}{3}\pi {\left( {\frac{a}{2}} \right)^2}.\frac{{a\sqrt 3 }}{2} = \frac{{\pi {a^3}\sqrt 3 }}{{24}}\)

Chọn đáp án C.

Câu 5: Gọi S là diện tích xung quanh của hình nón tròn xoay được sinh ra bởi đoạn thẳng AC’ của hình lập phương ABCD.A’B’C’D’ có cạnh b khi quay xung quang trục AA’. Diện tích S là:

A. \(\pi {b^2}\)

B. \(\pi {b^2}\sqrt 2 \)

C. \(\pi {b^2}\sqrt 3 \)

D. \(\pi {b^2}\sqrt 6 \)

Hướng dẫn giải:

\(S = \pi rl\) với \(r = b\sqrt 2 ;l = b\sqrt 3 \)vậy \(S = \pi {b^2}\sqrt 6 \)

Chọn đáp án D.

Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy\(SC = a\sqrt 6 \). Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:

A. \(\frac{{4\pi {a^3}}}{3}\)

B. \(\frac{{\pi {a^3}\sqrt 2 }}{3}\)

C. \(\frac{{\pi {a^3}\sqrt 3 }}{3}\)

D. \(\frac{{\pi {a^3}\sqrt 3 }}{6}\)

Hướng dẫn giải:

Ta có ngay \(AC = a\sqrt 2  \Rightarrow SA = \sqrt {S{C^2} - A{C^2}}  = \sqrt {6{a^2} - 2{a^2}}  = 2a\)

Hình nón tròn xoay được tạo thành là một hình nón có thể tích là:

\(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi A{C^2}.SA = \frac{1}{3}\pi .2{a^2}.2a = \frac{{4\pi {a^3}}}{3}\)

Chọn đáp án A.

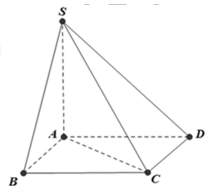
Câu 7: Một hình nón có đường sinh bằng a và góc ở đỉnh bằng 90⁰ . Cắt hình nón bằng mặt phẳng (P) đi qua đỉnh sao cho góc giữa (P) và mặt đáy hình nón bằng 60⁰ . Khi đó diện tích thiết diện là :

A. \(\frac{{\pi \sqrt 2 {a^2}}}{3}\)

B. \(\frac{{\pi \sqrt 3 }}{2}{a^2}\)

C. \(\frac{{2\pi }}{3}{a^2}\)

D. \(\frac{{3\pi }}{2}{a^2}\)

Hướng dẫn giải:

Gọi S là đỉnh hình nón,O là tâm đường tròn đáy; I là trung điểm AB , Góc tạo bởi mp thiết diện và đáy là góc SIO.

Suy luận được OA = OS = \(\frac{{a\sqrt 2 }}{2};SI = \frac{{a\sqrt 2 }}{{\sqrt 3 }};OI = \frac{{a\sqrt 6 }}{6};AI = \frac{a}{{\sqrt 3 }};AB = \frac{{2a}}{{\sqrt 3 }}\)

\({S_{td}} = \pi \frac{{\sqrt 2 {a^2}}}{3}\)

Chọn đáp án A.

Câu 8: Cho tứ diện đều ABCD. Khi quay tứ diện đó quanh trục AB có bao nhiêu hình nón khác nhau được tạo thành ?

A. Một

B. Hai

C. Ba

D. Không có hình nón nào

Hướng dẫn giải:

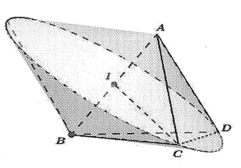
Khi quay ta được hình như bên cạnh, hình này được tạo thành từ hai hình nón.

Chọn đáp án B.

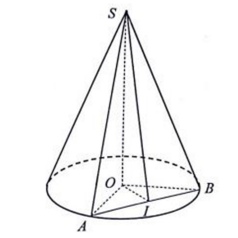
Câu 9: Cho hình nón có chiều cao h và góc ở đỉnh bằng 90⁰ . Thể tích của khối nón xác định bởi hình nón trên:

A. \(\frac{{\pi {h^3}}}{3}\)

B. \(\frac{{\sqrt 6 \pi {h^3}}}{3}\)

C. \(\frac{{2\pi {h^3}}}{3}\)

D. \(2\pi {h^3}\)

Hướng dẫn giải: Do góc ở đỉnh của hình nón bằng 90⁰ nên thiết diện qua trục hình nón là tam giác vuông cân. Suy ra bán kính đáy của hình nón là R = h

Thể tích khối nón là : \(V = \frac{1}{3}\pi {R^2}h = \frac{{\pi {h^3}}}{3}\)

Chọn đáp án A.

Câu 10: Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng 2 và  SAO = 30⁰ ; 0 SAB = 60⁰ . Tính diện tích xung quanh hình nón ?

A. \(4\pi \sqrt 3 \)

B. \(\frac{{3\pi \sqrt 2 }}{4}\)

C. \(2\pi \sqrt 3 \)

D. \(3\pi \sqrt 2 \)

Hướng dẫn giải: Gọi I là trung điểm của AB thì OI \( \bot \) AB, SI \( \bot \) AB, OI =  2

Lại có \(\left\{ {\begin{array}{*{20}{c}}{AO = SA.\cos SAO = SA.\frac{{\sqrt 3 }}{2}}\\{AI = SA.\cos SAI = \frac{{SA}}{2}}\end{array}} \right.\)

Từ đó ta có \(\frac{{AI}}{{AO}} = \frac{1}{{\sqrt 3 }}\)

Mặt khác \(\frac{{AI}}{{AO}} = \cos IAO \Rightarrow \sin IAO = \frac{{\sqrt 6 }}{3} = \frac{2}{{OA}} \Rightarrow OA = \sqrt 6 \)

Mà \(SA = \frac{{OA}}{{\cos 30}} = \sqrt 6 .\frac{2}{{\sqrt 3 }} = 2\sqrt 2 \)

Diện tích xung quanh cần tính là: \({S_{xq}} = \pi .OA.SA = 4\pi \sqrt 3 \)

Chọn đáp án A.

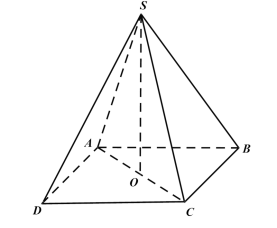
Câu 11: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc\(\angle SAB = {60^0}\). Thể tích của hình nón đỉnh S đáy là đường tròn ngoại tiếp ABCD là:

A. \(\frac{{\pi {a^3}\sqrt 3 }}{{12}}\)

B. \(\frac{{\pi {a^3}\sqrt 2 }}{{12}}\)

C. \(\frac{{\pi {a^3}\sqrt 2 }}{6}\)

D. \(\frac{{\pi {a^3}\sqrt 3 }}{6}\)

Hướng dẫn giải:

Tam giác SAB đều => SA = a;

\(SO = \sqrt {S{A^2} - A{O^2}}  = \sqrt {{a^2} - \frac{{2{a^2}}}{4}}  = \frac{{a\sqrt 2 }}{2}\)

\(R = AO = \frac{{a\sqrt 2 }}{2}\)

\( \Rightarrow V = \frac{1}{3}\pi {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2}.\frac{{a\sqrt 2 }}{2} = \pi .\frac{{{a^2}\sqrt 2 }}{{12}}\)

Chọn đáp án B.

Câu 12: Cho hình lập phương ABCD. A’B’C’D’ có cạnh bằng a. Một hình nón có đỉnh là tâm của hình vuông ABCD và có đường tròn đáy ngoại tiếp hình vuông A’B’C’D’. Diện tích xung quanh của hình nón đó là:

A. \(\frac{{\pi {a^2}\sqrt 3 }}{3}\)

B. \(\frac{{\pi {a^2}\sqrt 2 }}{2}\)

C. \(\frac{{\pi {a^2}\sqrt 5 }}{4}\)

D. \(\frac{{\pi {a^2}\sqrt 6 }}{2}\)

Hướng dẫn giải:

Hướng dẫn: Độ dài đường sinh bằng:

 \(\sqrt {{a^2} + {{\left( {\frac{1}{2}a} \right)}^2}}  = \frac{{a\sqrt 5 }}{2}\)

Diện tích xung quanh hình nón bằng:

\(\pi rl = \pi \frac{a}{2}\frac{{a\sqrt 5 }}{2} = \frac{{\pi {a^2}\sqrt 5 }}{4}\)

Chọn đáp án C.

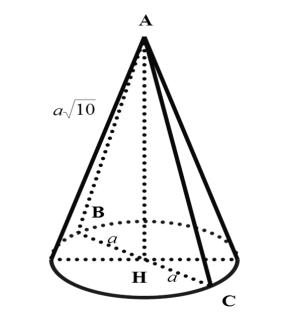
Câu 13: Trong không gian, cho tam giác ABC cân tại A, AB =\(a\sqrt {10} \), BC = 2a . Gọi H là trung điểm của BC. Tính thể tích V của hình nón nhận được khi quay tam giác ABC xung quanh trục AH.

A. \(V = 2\pi {a^3}\)

B. \(V = 3\pi {a^3}\)

C. \(V = 9\pi {a^3}\)

D. \(V = \pi {a^3}\)

Hướng dẫn giải:

+ Đường sinh \(l = AB = a\sqrt {10} \)

+ Bán kính đáy Þ đường cao $h=\sqrt{l^2-r^2}=3a$

+ Thể tíc\(r = \frac{{BC}}{2} = a\)h của hình nón tạo thành \(V = \frac{1}{3}\pi h{r^2} = \pi {a^3}\)

Chọn đáp án D.

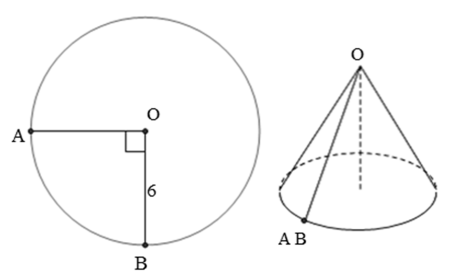
Câu 14: Cho hình tròn có bán kính là 6. Cắt bỏ \(\frac{1}{4}\) hình tròn giữa 2 bán kính OA, OB, rồi ghép 2 bán kính đó lại sao cho thành một hình nón (như hình vẽ). Thể tích khối nón tương ứng đó là :

A. \(\frac{{81\pi \sqrt 7 }}{8}\)

B. \(\frac{{9\pi \sqrt 7 }}{8}\)

C. \(\frac{{81\pi \sqrt 7 }}{4}\)

D. \(\frac{{9\pi \sqrt 7 }}{2}\)

Hướng dẫn giải:

\(r = \frac{{\frac{3}{4}.12\pi }}{{2\pi }} = \frac{9}{2};h = \sqrt {{l^2} - {r^2}}  = \frac{{3\sqrt 7 }}{2};V = \frac{1}{3}\pi {r^2}.h = \frac{{81\pi \sqrt 7 }}{8}\)

 Chọn đáp án A.

a