Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết và bài tập về mặt nón, tài liệu bao gồm 31 trang lý thuyết, bài tập và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Lý thuyết và bài tập về mặt nón có đáp án chi tiết

MỤC LỤC

A. KIẾN THỨC CẦN NHỚ

B. BÀI TẬP MẪU

C. BÀI TẬP TỰ LUYỆN

D. BÀI TẬP TRẮC NGHIỆM

1. Tính diện tích, thể tích mặt nón đơn thuần

2. Quay tam giác

3. Mặt nón ngoại tiếp khối đa diện

MẶT NÓN

A. KIẾN THỨC CẦN NHỚ

1. Mặt nón tròn xoay

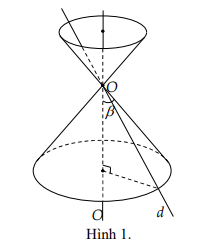
Trong mặt phẳng (P) , cho hai đường thẳng d và \(\Delta \) cắt nhau tại O và chúng tạo thành góc \(\beta \) với\({0^ \circ } < \beta  < {90^ \circ }\). Khi quay (P) xung quanh trục \(\Delta \) với góc \(\beta \) không thay đổi được gọi là mặt nón tròn xoay (gọi tắt là mặt nón) đỉnh O (hình 1). Đường thẳng \(\Delta \)  gọi là trục, đường thẳng d được gọi là đường sinh và góc 2\(\beta \) gọi là góc ở đỉnh.

2. Hình nón tròn xoay

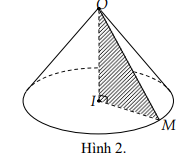
Cho \(\Delta \) OIM vuông tại I quay quanh cạnh góc vuông OI thì đường gấp khúc OIM tạo thành một hình, gọi là hình nón tròn xoay (gọi tắt là hình nón) (hình 2).

-  Đường thẳng OI gọi là trục, O là đỉnh, OI gọi là đường cao và OM gọi là đường sinh của hình nón.

- Hình tròn tâm I , bán kính r = IM là đáy của hình nón.

-  Phần mặt tròn xoay sinh bởi các điểm trên cạnh OM khi quay quanh OI gọi là mặt xung quanh của hình nón.

Khối nón tròn xoay (gọi tắt là khối nón) là phần không gian được giới hạn bởi một hình nón tròn xoay, kể cả hình nón đó.

 3. Một số tính chất

a) Nếu cắt hình nón bởi mặt phẳng (P) đi qua đỉnh thì có các trường hợp sau:

· (P) cắt hình nón theo hai đường sinh Þgiao tuyến là tam giác cân.

· (P) tiếp xúc với mặt nón theo một đường sinh ((P) là mặt phẳng tiếp diện của hình nón).

b) Nếu cắt hình nón bởi mặt phẳng (P) không đi qua đỉnh thì có các trường hợp sau:

· Nếu (P) vuông góc với trục hình nón Þ giao tuyến là một đường tròn.

· Nếu (P) song song với 2 đường sinh hình nón Þ giao tuyến là một nhánh của hypebol.

· Nếu (P) song song với 1 đường sinh hình nón Þ giao tuyến là một đường parabol.

4. Công thức diện tích và thể tích của hình nón

Cho hình nón có chiều cao là h , bán kính đáy r và đường sinh là l thì có:

- Diện tích xung quanh: \({S_{xq}} = \pi rl\)

- Diện tích toàn phần hình nón: \({S_{tp = }}{S_{xq}} + {S_{day}} = \pi rl + \pi {r^2}\)

- Thể tích khối nón: V_nón = \(\frac{1}{3}\)S_đáy . h = \(\frac{1}{3}\pi {r^2}h\)

B. BÀI TẬP MẪU

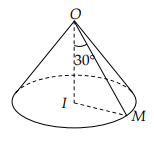
Ví dụ 1: Cho tam giác vuông OIM quanh cạnh góc vuông OI tạo thành một hình nón tròn xoay. Biết góc \(\widehat {IOM} = {30^0}\)và cạnh IM = a . Tính diện tích xung quanh của hình nón tròn xoay và thể tích của khối nón tròn xoay được tạo nên bởi hình nón tròn xoay trên.

Giải: Ta có: r = IM =a

\(\begin{array}{l}l = OM = \frac{{IM}}{{\sin \widehat {IOM}}} = 2a,\\h = OI = \sqrt {O{M^2} - {\mathop{\rm I}\nolimits} {M^2}}  = a\sqrt 3 \end{array}\)

Diện tích xung quanh của hình nón:

 \({S_{xq}} = \pi rl = \pi a.2a = 2\pi {a^2}\)

Thể tích của khối nón:

\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {a^2}a\sqrt 3  = \frac{{\pi {a^3}\sqrt 3 }}{3}\)

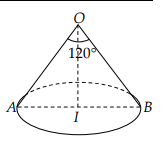
Ví dụ 2: Một hình nón có đường kính đáy là \(2a\sqrt 3 \), góc ở đỉnh là\({120^0}\). Tính diện tích toàn phần của hình nón và thể tích của khối nón trên.

Giải: Ta có \(r = IA = a\sqrt 3 ,\widehat {IOA} = {60^0}\)nên

\(\begin{array}{l}l = OA = \frac{{IA}}{{\sin {{60}^0}}} = \frac{{a\sqrt 3 }}{{\frac{{\sqrt 3 }}{2}}} = 2a,\\h = OI = \sqrt {O{A^2} - I{A^2}}  = \sqrt {4{a^2} - 3{a^2}}  = a\end{array}\)

Diện tích xung quanh của hình nón:

 \({S_{xq}} = \pi rl =  = \pi a\sqrt 3 .2a = 2\pi {a^2}\sqrt 3 \)

Diện tích đáy của hình nón: S_đáy = \(\pi {r^2} = 3\pi {a^2}\)

Diện tích toàn phần của hình nón:

S_tp = S_xq + S_đáy = \(2\pi {a^2}\sqrt 3  + 3\pi {a^2} = \left( {2\sqrt 3  + 3} \right)\pi {a^2}\)

Thể tích của khối nón:

 V = \(\frac{1}{3}\)S_đáy . h = \(\frac{1}{3}3\pi {a^2}.a = \pi {a^3}\)

Ví dụ 3: Cho hình nón có chiều cao h = 20 cm, bán kính đáy r = 25 cm. Mặt phẳng \(\left( \alpha  \right)\) đi qua đỉnh cắt hai đường sinh của hình nón. Biết khoảng cách từ tâm của đáy đến mặt phẳng \(\left( \alpha  \right)\) là 12 cm. Tính diện tích thiết diện đó.

Giải:

Ta có \(\left( \alpha  \right)\) cắt hình nón theo thiết diện là tam giác cân OAB với A B, là hai điểm nằm trên đường tròn đáy.

Gọi H là trung điểm AB khi đó IH ^ AB  .

 Mà OI ^ AB suy ra AB ^ (OIH)   (1).

Kẻ IK ^ OH , K nằm trên OH

Từ (1) suy ra IK ^ AB  . Do đó IK ^ (OAB). Theo giả thiết IK = 12 cm.

Tam giác OIH vuông tại I nên

\(\begin{array}{l}\frac{1}{{I{K^2}}} = \frac{1}{{I{H^2}}} + \frac{1}{{O{I^2}}}\\ \Rightarrow IH = \frac{{OI.IK}}{{\sqrt {O{I^2} - I{K^2}} }} = \frac{{20.12}}{{\sqrt {{{20}^2} - {{12}^2}} }} = 15cm\end{array}\)

\(OH = \sqrt {O{I^2} + I{H^2}}  = \sqrt {{{20}^2} + {{15}^2}}  = 25cm\)

\(\begin{array}{l}AH = \sqrt {I{A^2} - I{H^2}}  = \sqrt {{{20}^2} - {{15}^2}}  = 20cm\\ \Rightarrow AB = 40cm\end{array}\)

Diện tích thiết diện:

\(s = \frac{1}{2}OH.AB = \frac{1}{2}.25.40 = 500c{m^2}\)

C. BÀI TẬP TỰ LUYỆN Bài 1.

Cho hình nón đỉnh S có thiết diện đi qua trục là tam giác vuông cân SAB có cạnh huyền bằng \(a\sqrt 2 \). Tính diện tích toàn phần của hình nón và thể tích của khối nón tương ứng.

Đáp án: \({S_{tp}} = \frac{{\pi {a^2}\left( {1 + \sqrt 2 } \right)}}{2},V = \frac{{\pi {a^3}\sqrt 2 }}{{12}}\)

Bài 2. Cho hình nón tròn xoay có đỉnh là S có O là tâm của đường tròn đáy, đường sinh bằng \(a\sqrt 2 \)và góc giữa đường sinh và mặt phẳng đáy bằng 60⁰ . Tính diện tích xung quanh S_xq của hình nón và thể tích của khối nón tương ứng.

Đáp án: \({S_{xq}} = \pi {a^2};V = \frac{{\pi {a^3}\sqrt 6 }}{{12}}\)

Bài 3. Cho hình nón tròn xoay có thiết diện qua trục là một tam giác vuông cân có diện tích bằng 2a². Tính diện tích xung quanh của hình nón và thể tích của khối nón tướng ứng.

Đáp án: \({S_{xq}} = 2\pi {a^2}\sqrt 2 ;V = \frac{{2\sqrt 2 \pi {a^3}}}{3}\)

Bài 4. Cho hình lăng trụ tứ giác đều ABCD. A’B’C’D’ có cạnh đáy bằng a , chiều cao 2a . Biết rằng O’ là tâm của A’B’C’D’ và (C) là đường tròn nội tiếp đáy ABCD . Tính diện tích xung quanh của hình nón có đỉnh O’ và đáy (C).

Đáp án: \({S_{xq}} = \frac{{3\pi {a^2}}}{2}\)

Bài 5. Cho hình nón đỉnh O , chiều cao là h . Một khối nón khác có đỉnh là tâm của đáy và có đáy là là một thiết diện song song với đáy của hình nón đỉnh O đã cho (hình vẽ). Tính chiều cao x của khối nón này để thể tích của nó lớn nhất, biết 0 < x < h .

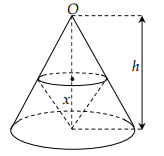
Đáp án: \(x = \frac{h}{3}\)

D. BÀI TẬP TRẮC NGHIỆM

1. Tính diện tích, thể tích mặt nón đơn thuần.

Câu 1: [2H2-1] (Chuyên Thái Bình, lần 3 năm 2017) Cho hình nón có bán kính đáy là 4a , chiều cao là 3a . Diện tích xung quanh hình nón bằng

A.\(24\pi {a^2}\).

B.\(20\pi {a^2}\).

C.\(40\pi {a^2}\).

D.\(12\pi {a^2}\).

 Hướng dẫn giải:

Chọn B.

\({S_{xq}} = \pi rl;{l^2} = {\left( {3a} \right)^2} + {\left( {4a} \right)^2} = {\left( {5a} \right)^2} \Rightarrow l = 5a \Rightarrow {S_{xq}} = 20\pi {a^2}\)

Câu 2: [2H2-2] (Chuyên Nguyễn Quang Diệu, lần 1 năm 2017) Một hình nón có đường sinh bằng đường kính đáy. Diện tích đáy của hình nón bằng \(9\pi \) . Tính đường cao h của hình nón.

A. \(h = 3\sqrt 3 \)

B. \(h = \sqrt 3 \)

C. \(h = \frac{{\sqrt 3 }}{2}\)

D. \(h = \frac{{\sqrt 3 }}{3}\)

Hướng dẫn giải:

Chọn A.

Ta có \(l = 2R\)và \(S = 9\pi  \Rightarrow \pi {R^2} = 9\pi  \Rightarrow R = 3\)

\( \Rightarrow h = AO = \sqrt {{6^2} - {3^3}}  = 3\sqrt 3 \)

Câu 3: [2H2-2] (THPT Lê Hồng Phong, năm 2017): Một hình nón có thiết diện qua trục là tam giác đều cạnh a. Thể tích khối nón là

A. \(\frac{{{a^3}\sqrt 3 \pi }}{{12}}\)

B. \(\frac{{{a^3}\sqrt 3 \pi }}{{24}}\)

C. \(\frac{{{a^3}\sqrt 2 \pi }}{{24}}\)

D. \(\frac{{{a^3}\sqrt 2 \pi }}{{12}}\)

Hướng dẫn giải:

Chọn B. Ta có tam giác SAB đều cạnh a , \(SO = \frac{{a\sqrt 3 }}{2},r = OB = \frac{a}{2}\)

Vậy thể tích khối nón là

\(V = \frac{1}{3}\pi {r^2}.SO = \frac{{\pi {a^2}}}{{12}}.\frac{{a\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 \pi }}{{24}}\)

Câu 4: [2H2-2] (Chuyên ĐHSP Hà Nội, năm 2017): Cho hình nón có chiều cao bằng 3cm , góc giữa trục và đường sinh bằng 60° . Thể tích của khối nón là

A. \(9\pi c{m^3}\)

B. \(3\pi c{m^3}\).

C. \(18\pi c{m^3}\)

D. \(27\pi c{m^3}\)