Tailieumoi.vn xin giới thiệu Bài tập Toán 5 Chương 1 Bài 9: Hỗn số (tiếp). Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 5. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 9: Hỗn số (tiếp). Mời các bạn đón xem:

Bài tập Toán 5 Chương 1 Bài 9: Hỗn số (tiếp)

A. Bài tập Hỗn số (tiếp)

I. Bài tập trắc nghiệm

Khoanh tròn vào chữ cái trước câu trả lời đúng:

Câu 1: Phân số thích hợp chỉ phần tô đậm của hình sau là:

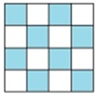
A. $\frac{3}{2}$

B. $\frac{6}{16}$

C. $\frac{1}{2}$

D. $\frac{9}{16}$

Câu 2: Viết thương $47:28$dưới dạng phân số ta được:

A. $\frac{47}{10}$và $\frac{28}{10}$

B. $\frac{47}{28}$

C. $\frac{28}{47}$

D. $1\frac{47}{28}$

Câu 3: Rút gọn phân số sau: $\frac{21}{30}$

A. $\frac{7}{6}$

B. $\frac{3}{5}$

C. Không rút gọn được

D. $\frac{7}{10}$

Câu 4: Trong các phân số sau, phân số nào là phân số thập phân:

$\frac{10}{7};\frac{4}{10};\frac{100}{51};\frac{65}{1000};\frac{4}{3000}$

A. $\frac{10}{7};\frac{100}{51}$

B. $\frac{4}{10}$

C. $\frac{65}{1000};\frac{4}{3000}$

D. $\frac{4}{10};\frac{65}{1000}$

Câu 5: Chuyển phân số sau thành phân số thập phân: $\frac{11}{25}=\dots$

A. $\frac{44}{10}$

B. $\frac{11}{10}$

C. $\frac{11}{1000}$

D. $\frac{44}{100}$

Câu 6: Hỗn số thích hợp biểu diễn số phần hình tròn được tô màu điền vào chỗ chấm là :

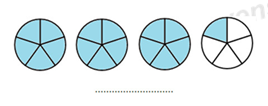
A. $2\frac{6}{12}$

B. $3\frac{1}{5}$

C. $4\frac{1}{5}$

D. $3\frac{2}{5}$

Câu 7: Tính: $3\frac{1}{2}+2\frac{2}{5}=\dots$

A. $\frac{37}{10}$

B. $\frac{52}{5}$

C. $\frac{59}{10}$

D. $\frac{42}{5}$

Câu 8: Mẹ làm 20 chiếc bánh rán rất ngon, trong đó có $\frac{2}{5}$số bánh rán là bánh ngọt, $\frac{1}{4}$số bánh rán là bánh mặn, số bánh rán còn lại là bánh vừng. Hỏi mẹ đã làm bao nhiêu chiếc bánh vừng?

A. 7

B. 8

C. 6

D. 10

II. Bài tập tự luận

Câu 1. Tính:

$$\begin{gathered} \frac{1}{3}+\frac{1}{4}=\dots \\ \frac{6}{5}-\frac{6}{10}=\dots \\ \frac{2}{5}\times \frac{3}{8}=\dots \\ \frac{9}{11}:\frac{21}{15}=\dots \end{gathered}$$

Câu 2. Tính:

$$\begin{gathered} \frac{5}{11}:\frac{5}{3}+\frac{7}{55}=\dots \\ 7-\frac{5}{6}\times 5=\dots \end{gathered}$$

Câu 3: Phương, Hòa, Dương cùng hái dâu tây. Phương hái được 1 hộp và $\frac{1}{2}$hộp, Hòa hái được 1 hộp và $\frac{3}{4}$hộp, Dương hái được 1 hộp và $\frac{3}{4}$hộp.

a) Viết hỗn số biểu diễn số hộp dâu tây mà mỗi bạn hái được:

b) Tính số hộp dâu tây cả ba bạn hái được:

c) Nếu đem tất cả số dâu tây hái được chia đều cho 3 bạn thì mỗi bạn được mấy phần hộp dâu tây?

Câu 4. Chuyển hỗn số thành phân số rồi thực hiện phép tính:

a) $3\frac{1}{2}+2\frac{2}{5}=\dots$

b) $5\frac{3}{8}-1\frac{2}{3}=\dots$

c) $6\frac{3}{4}\times 3\frac{7}{13}=\dots$

d) $9\frac{5}{6}:8\frac{1}{7}=\dots$

Câu 5. So sánh các hỗn số:

a) $7\frac{3}{7}\dots 6\frac{3}{7}$

b) $3\frac{2}{3}\dots 3\frac{4}{5}$

c) $7\frac{5}{6}\dots 8\frac{5}{6}$

d) $7\frac{4}{12}\dots 7\frac{1}{3}$

III. Bài tập vận dụng

Câu 1: Chuyển các phân số sau thành hỗn số rồi thực hiện phép tính:

a,	b,	c,
d,	e,	f,

Câu 2: Tìm X, biết:

a,

b,

c,

Câu 3: Chuyển các phân số sau thành hỗn số (theo mẫu)

Mẫu:  Có = 2 (dư 3). Vậy 

a,

b,

c,

d,

e,

Câu 4:

a) Đọc các phân số sau:

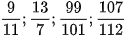
b) Viết các phân số sau:

– Năm phần mười ba

– Hai mươi bảy phần bốn mươi mốt

– Một trăm linh sáu phần một trăm bảy mươi chín.

Đáp án:

Phân số 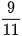 đọc là chín phần mười một.

Còn lại, bạn đọc tự làm.

Phân số 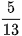 đọc là năm phần mười ba.

Còn lại, bạn đọc tự làm.

Câu 5:

a) Viết thương các phép chia sau dưới dạng phân số

b) Cho các phân số sau:

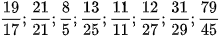
Hãy viết các phân số nhỏ hơn 1 bên trái, các phân số bằng 1 ở giữa và các phân số lớn hơn 1 bên tay phải. Giữa mỗi phần để một khoảng cách rộng hơn khoảng cách hai phân số thường để dễ phân biệt.

Đáp án:

a) 8 : 9 viết là 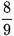; 24 : 6 viết là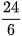 

Còn lại, bạn đọc tự làm.

b)

Câu 6:

a) Hãy so sánh mỗi cặp phân số sau bằng 2 cách:

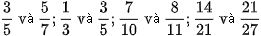
b) Hãy so sánh mỗi cặp phân số sau bằng 3 cách:

Đáp án:

a)

Cách 1: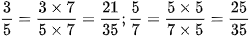 

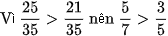
Cách 2: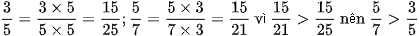 

Còn lại, bạn đọc tự làm.

b)

Cách 1: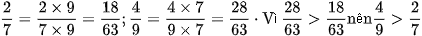 

Cách 2: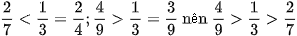 

Còn lại, bạn đọc tự làm.

B. Lý thuyết Hỗn số (tiếp)

1. Phép cộng và phép trừ hỗn số

* Để thực hiện phép cộng và phép trừ hỗn số, ta có hai cách làm sau:

Cách 1: Chuyển hỗn số về phân số

+ Muốn cộng (hoặc trừ) hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi cộng (hoặc) trừ hai phân số vừa chuyển đổi.

Ví dụ: Thực hiện phép tính:

a) $4\frac{1}{5}+1\frac{6}{15}$

b) $5\frac{1}{2}-3\frac{1}{4}$

Lời giải:

a) $4\frac{1}{5}+1\frac{6}{15}$

$$\begin{gathered} =\frac{21}{5}+\frac{21}{15} \\ =\frac{63}{15}+\frac{21}{15}=\frac{84}{15} \end{gathered}$$

b) $5\frac{1}{2}-3\frac{1}{4}$

$$\begin{gathered} =\frac{11}{2}-\frac{13}{4} \\ =\frac{22}{4}-\frac{13}{4}=\frac{9}{4} \end{gathered}$$

Cách 2: Tách hỗn số thành phần nguyên và phần phân số, sau đó thực hiện phép cộng (trừ) phần nguyên và phép cộng (trừ) phần phân số.

Ví dụ: Thực hiện phép tính:

a) $1\frac{1}{6}+2\frac{7}{12}$

b) $5\frac{3}{4}-2\frac{1}{8}$

Lời giải:

a) $1\frac{1}{6}+2\frac{7}{12}$

$$\begin{gathered} =\left(1+2\right)+\left(\frac{1}{6}+\frac{7}{12}\right) \\ =3+\frac{9}{12}=3+\frac{3}{4}=3\frac{3}{4} \end{gathered}$$

b) $5\frac{3}{4}-2\frac{1}{8}$

$$\begin{gathered} =\left(5-2\right)+\left(\frac{3}{4}-\frac{1}{8}\right) \\ =3+\frac{5}{8}=3\frac{5}{8} \end{gathered}$$

2. Phép nhân và phép chia hỗn số

+ Để thực hiện nhân (hoặc chia) hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi nhân (hoặc chia) hai phân số vừa chuyển đổi.

Ví dụ: Thực hiện phép tính:

a) $4\frac{7}{8}\times 1\frac{3}{13}$

b) $4\frac{2}{5}:1\frac{7}{15}$

Lời giải:

a) $4\frac{7}{8}\times 1\frac{3}{13}$

$$\begin{gathered} =\frac{39}{8}\times \frac{16}{13}=\frac{39\times 16}{8\times 13} \\ =\frac{3\times 2}{1\times 1}=6 \end{gathered}$$

b) $4\frac{2}{5}:1\frac{7}{15}$

$$\begin{gathered} =\frac{22}{5}:\frac{22}{15} \\ =\frac{22}{5}\times \frac{15}{22}=3 \end{gathered}$$

3. So sánh hỗn số

* Để thực hiện so sánh hỗn số, ta có hai cách dưới đây:

Cách 1: Chuyển hỗn số về phân số: để so sánh hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi so sánh hai phân số vừa chuyển đổi.

Ví dụ: So sánh hai hỗn số: $5\frac{1}{4}$ và $2\frac{2}{3}$

Lời giải:

Ta có: $5\frac{1}{4}=\frac{21}{4}$ và $2\frac{2}{3}=\frac{8}{3}$

Quy đồng mẫu số hai phân số, ta có:

$$\begin{gathered} \frac{21}{4}=\frac{21\times 3}{4\times 3}=\frac{63}{12} \\ \frac{8}{3}=\frac{8\times 4}{3\times 4}=\frac{32}{12} \end{gathered}$$

Vì $\frac{63}{12}>\frac{32}{12}$ nên $5\frac{1}{4}>2\frac{2}{3}$

Cách 2: So sánh phần nguyên và phần phân số. Khi so sánh hai hỗn số:

- Hỗn số nào có phần nguyên lớn hơn thì hỗn số đó lớn hơn và ngược lại hỗn số nào có phần nguyên nhỏ hơn thì hỗn số đó nhỏ hơn

- Nếu hai phần nguyên bằng nhau thì ta so sánh phần phân số, hỗn số nào có phần phân số lớn hơn thì hỗn số đó lớn hơn.

Ví dụ: So sánh các hỗn số sau:

a) $2\frac{1}{4}$ và $3\frac{5}{6}$

b) $4\frac{5}{12}$ và $4\frac{5}{8}$

Lời giải:

a) $2\frac{1}{4}$ và $3\frac{5}{6}$

Hỗn số $2\frac{1}{4}$ có phần nguyên bằng 2 và hỗn số $3\frac{5}{6}$ có phần nguyên bằng 3

Vì 2 < 3 nên $2\frac{1}{4}<3\frac{5}{6}$.

b) $4\frac{5}{12}$ và $4\frac{5}{8}$

Hai hỗn số có cùng phần nguyên nên ta so sánh phần phân số của hai hỗn số

Vì $\frac{5}{12}<\frac{5}{8}$ nên $4\frac{5}{12}<4\frac{5}{8}$