Với tóm tắt lý thuyết Toán lớp 5 Hỗn số (tiếp theo) hay, chi tiết cùng với 10 bài tập chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 5.
Lý thuyết Hỗn số (tiếp theo) lớp 5 hay, chi tiết
A. Lý thuyết Hỗn số
1. Phép cộng và phép trừ hỗn số
* Để thực hiện phép cộng và phép trừ hỗn số, ta có hai cách làm sau:
Cách 1: Chuyển hỗn số về phân số
+ Muốn cộng (hoặc trừ) hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi cộng (hoặc) trừ hai phân số vừa chuyển đổi.
Ví dụ: Thực hiện phép tính:
|
a) |
b) |
Lời giải:
a) 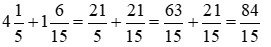
b) 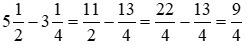
Cách 2: Tách hỗn số thành phần nguyên và phần phân số, sau đó thực hiện phép cộng (trừ) phần nguyên và phép cộng (trừ) phần phân số.
Ví dụ: Thực hiện phép tính:
|
a) |
b) |
Lời giải:
a) 
b) 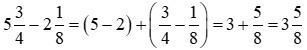
2. Phép nhân và phép chia hỗn số
+ Để thực hiện nhân (hoặc chia) hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi nhân (hoặc chia) hai phân số vừa chuyển đổi.
Ví dụ: Thực hiện phép tính:
|
a) |
b) |
Lời giải:
a) 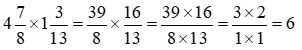
b) 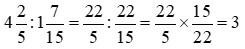
3. So sánh hỗn số
* Để thực hiện so sánh hỗn số, ta có hai cách dưới đây:
Cách 1: Chuyển hỗn số về phân số: để so sánh hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi so sánh hai phân số vừa chuyển đổi.
Ví dụ: So sánh hai hỗn số: 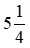 và
và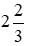
Lời giải:
Ta có: 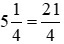 và
và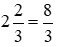
Quy đồng mẫu số hai phân số, ta có:
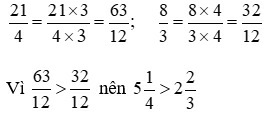
Cách 2: So sánh phần nguyên và phần phân số. Khi so sánh hai hỗn số:
- Hỗn số nào có phần nguyên lớn hơn thì hỗn số đó lớn hơn và ngược lại hỗn số nào có phần nguyên nhỏ hơn thì hỗn số đó nhỏ hơn
- Nếu hai phần nguyên bằng nhau thì ta so sánh phần phân số, hỗn số nào có phần phân số lớn hơn thì hỗn số đó lớn hơn.
Ví dụ: So sánh các hỗn số sau:
|
a) |
b) |
Lời giải:
a) 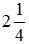 và
và 
Hỗn số 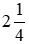 có phần nguyên bằng 2 và hỗn số
có phần nguyên bằng 2 và hỗn số 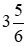 có phần nguyên bằng 3
có phần nguyên bằng 3
Vì 2 < 3 nên 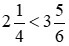
b) 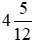 và
và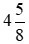
Hai hỗn số có cùng phần nguyên nên ta so sánh phần phân số của hai hỗn số
Vì 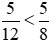 nên
nên 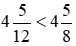
B. Bài tập Hỗn số
Câu 1: Phần phân số của hỗn số 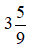
Phần phân số của hỗn số
Câu 2: Phân số 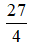
Ta có: 27 : 4 = 6 dư 3.
Câu 3: Chuyển hỗn số 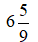
Câu 4: Chuyển hỗn số 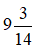
Câu 5: Chuyển hỗn số 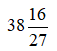
Câu 6: Hỗn số gồm bao nhiêu thành phần?
A. Một thành phần, đó là phần nguyên
B. Một thành phần, đó là phần phân số
C. Hai thành phần, đó là phần nguyên và phần phân số.
Hỗn số có hai thành phần là phần nguyên và phần phân số.
Câu 7: Chọn hỗn số trong các đáp án sau:
Hỗn số có hai thành phần là phần nguyên và phần phân số. Vậy hỗn số là 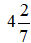
Câu 8: Chọn số thích hợp điền vào chỗ chấm:
Phần nguyên của hỗn số 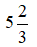
A. 5
B. 3
C. 4
D. 2
E. 1
Phần nguyên của hỗn số 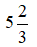
Vậy số thích hợp đặt vào ô trống là 5.
Câu 9: Hỗn số “mười ba và hai mươi lăm phần ba mươi tám” được viết là:
Hỗn số “mười ba và hai mươi lăm phần ba mươi tám” được viết là 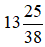
Câu 10: Chọn số thích hợp đặt vào ô trống:
Khi chuyển phân số 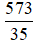
A. 17
B. 18
C. 16
D. 15
E. 14