50 Bài tập Tính chất cơ bản của phân số (có đáp án)- Toán 5

Trần Thị Hồng Ngày: 08-03-2024 Lớp 5

Tải xuống 3 1.5 K 22

Tailieumoi.vn xin giới thiệu Bài tập Toán 5 Chương 1 Bài 2: Ôn tập Tính chất cơ bản của phân số. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 5. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 2: Ôn tập Tính chất cơ bản của phân số. Mời các bạn đón xem:

Bài tập Toán 5 Chương 1 Bài 2: Ôn tập Tính chất cơ bản của phân số

A. Bài tập Tính chất cơ bản của phân số

I. Bài tập trắc nghiệm

Câu 1: Khoanh vào chữ cái đặt trước kết quả đúng:

Phân số chỉ phần được tô màu trong hình vẽ là:

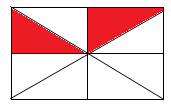
Tài liệu VietJack

A. $\frac{1}{4}$

B. $\frac{1}{2}$

C. $\frac{1}{8}$

D. $\frac{1}{6}$

Câu 2: Số thích hợp được điền vào chỗ chấm $983 : 389 = \frac{.....}{389}$ là:

A. 389

B. 983

C. 938

D. 398

Câu 3: Phân số $\frac{18}{25}$ được đọc là:

A. Mười tám phần hai mươi năm

B. Hai mươi lăm phần mười tám

C. Hai lăm phần mười tám

D. Mười tám phần hai mươi lăm

Câu 4: Phép tính nào đúng tương ứng với phân số $\frac{4}{7} = ?$

A. $4 : 7$

B. $7 : 4$

C. $4 \times 7$

D. $4 + 7$

Câu 5: Phân số biểu diễn số tự nhiên 2018 là:

A. $\frac{2018}{2}$

B. $\frac{1}{2018}$

C. $\frac{2018}{1}$

D. $\frac{2018}{0}$

Câu 6: Trong các đáp án sau, đáp án nào viết sai?

A. $0 = \frac{0}{21}$

B. $0 = \frac{0}{1}$

C. $0 = \frac{0}{2018}$

D. $0 = \frac{2018}{0}$

Câu 7: Chọn đáp án đúng trong các đáp án sau:

A. $1 = \frac{19}{9}$

B. $1 = \frac{20}{10}$

C. $1 = \frac{0}{1}$

D. $1 = \frac{15}{15}$

Câu 8: Phân số “Hai mươi chín phần bốn mươi hai” được viết là:

A. $\frac{29}{42}$

B. $\frac{42}{29}$

C. $\frac{92}{24}$

D. $\frac{29}{24}$

II. Bài tập tự luận

Câu 1:

a) Đọc các phân số sau :

$\frac{5}{18}$ : ………………………………………………………………………

$\frac{17}{45}$ : ………………………………………………………………………

$\frac{15}{7}$ : ………………………………………………………………………

b) Viết các phân số sau :

Bốn phần năm : …………………………………………………………

Ba mươi lăm phần bốn mươi tám : ……………………………………..

Bảy mươi tám phần hai trăm linh ba : ………………………………….

Câu 2: Viết số thích hợp vào chỗ chấm :

a) $\frac{5}{9} = \frac{.....}{36}$ $\frac{24}{60} = \frac{2}{.....}$

b) $\frac{7}{.....} = \frac{28}{44}$ $\frac{50}{150} = \frac{1}{.....}$

Câu 3: Quy đồng mẫu số các phân số sau:

a) $\frac{5}{6}$ và $\frac{3}{8}$

b) $\frac{5}{7}$ và $\frac{4}{9}$

c) $\frac{3}{8}$ và $\frac{7}{24}$

d) $\frac{3}{4}$ và $\frac{7}{6}$

Câu 4:

a) Viết các phân số sau theo thứ tự từ bé đến lớn : $\frac{3}{5}$ ; $\frac{4}{7}$ ; $\frac{2}{3}$

b) Viết các phân số sau theo thứ tự từ lớn đến bé: $\frac{1}{2}$ ; $\frac{4}{5}$ ; $\frac{5}{7}$

Câu 5: Chỉ ra các cặp phân số bằng nhau trong các phân số sau:

$\frac{36}{54}$ ; $\frac{5}{7}$ ; $\frac{27}{45}$ ; $\frac{6}{8}$ ; $\frac{35}{49}$ ; $\frac{3}{5}$ ; $\frac{27}{36}$ ; $\frac{2}{3}$

III. Bài tập vận dụng

Câu 1: Nêu tính chất cơ bản của phân số

Câu 2: Rút gọn các phân số sau: $\frac{5}{{15}};\frac{4}{{24}};\frac{9}{3};\frac{{10}}{{12}};\frac{8}{{16}}$

Câu 3: Quy đồng mẫu số các phân số dưới đây:

$\frac{1}{3}$ và $\frac{5}{7}$

$\frac{7}{{10}}$ và $\frac{9}{2}$

$\frac{5}{1}$ và $\frac{6}{9}$

$\frac{4}{{11}}$ và $\frac{9}{{22}}$

Câu 4: Tìm các phân số bằng nhau trong các phân số dưới đây:

$\frac{4}{3};\frac{7}{{12}};\frac{5}{6};\frac{{25}}{{30}};\frac{{21}}{{36}};\frac{{12}}{9};\frac{{100}}{{120}};\frac{{40}}{{30}}$

B. Lý thuyết Tính chất cơ bản của phân số

1. Tính chất cơ bản của phân số

- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

- Nếu chia hết cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

Ví dụ: $\frac{3}{4} = \frac{3 \times 2}{4 \times 2} = \frac{6}{8}; \frac{12}{20} = \frac{12 : 4}{20 : 4} = \frac{3}{5}$

3. Ứng dụng tính chất cơ bản của phân số

Dạng 1: Rút gọn phân số

Bước 1: Xét xem cả tử số và mẫu số của phân số đó cùng chia hết cho số tự nhiên nào lớn hơn 1

Bước 2: Chia cả tử số và mẫu số của phân số đó cho số vừa tìm được

Bước 3: Cứ làm thế cho đến khi tìm được phân số tối giản

Chú ý:

Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho số nào lớn hơn 1

Ví dụ: $\frac{9}{15} = \frac{9 : 3}{15 : 3} = \frac{3}{5}$

Dạng 2: Quy đồng mẫu số các phân số

a) Trường hợp mẫu số chung bằng tích của hai mẫu số của hai phân số đã cho

Bước 1: Lấy cả tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai

Bước 2: Lấy cả tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất

Ví dụ: Quy đồng hai phân số $\frac{3}{4}$ và $\frac{7}{3}$

MSC: 12

$\begin{array}{l} \frac{3}{4} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12} \\ \frac{7}{3} = \frac{7 \times 4}{3 \times 4} = \frac{28}{12} \end{array}$

b) Mẫu số của một trong các phân số chia hết cho mẫu số của các phân số còn lại

Bước 1: Lấy mẫu số chung là mẫu số mà chia hết cho mẫu số của các phân số còn lại

Bước 2: Tìm thừa số phụ

Bước 3: Nhân cả tử số và mẫu số của các phân số còn lại với thừa số phụ tương ứng

Bước 4: Giữ nguyên phân số có mẫu số chia hết cho mẫu số của các phân số còn lại

Ví dụ: Quy đồng mẫu số hai phân số $\frac{15}{16}$ và $\frac{3}{8}$ .

MSC = 16

$\begin{array}{l} \frac{15}{16} = \frac{15}{16} \\ \frac{3}{8} = \frac{3 \times 2}{8 \times 2} = \frac{6}{16} \end{array}$

Tài liệu có 3 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm

Tài Liệu Xem Nhiều

pdf 50 Bài tập Hỗn số (có đáp án)- Toán 5
2 51.4 K 1.1 K
pdf Một lớp học có 18 nữ và 12 nam. Hỏi số học sinh nam chiếm bao nhiêu phần trăm số học sinh cả lớp
1 40.2 K 3
pdf Bộ 40 Đề thi Toán lớp 5 Học kì 2 năm 2024 có đáp án
19 40 K 726
pdf Tìm tỉ số phần trăm của: 25 và 40
1 28.4 K 4
pdf 24 bài toán chuyển động môn Toán lớp 5
6 26.4 K 541