Tailieumoi.vn xin giới thiệu Bài tập Toán 5 Chương 1 Bài 6: Ôn tập: Phép cộng và phép trừ hai phân sốố. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 5. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 6: Ôn tập: Phép cộng và phép trừ hai phân số. Mời các bạn đón xem:

Bài tập Toán 5 Chương 1 Bài 6: Ôn tập phép cộng, phép trừ hai phân số

A. Bài tập Ôn tập: Phép cộng và phép trừ hai phân số

I. Bài tập trắc nghiệm

Câu 1: Kết quả của phép tính $\frac{1}{7}+\frac{2}{7}$ là:

A. $\frac{3}{7}$

B. $\frac{3}{14}$

C. $\frac{2}{49}$

D. $\frac{3}{49}$

Câu 2: Kết quả của phép tính $\frac{8}{15}-\frac{4}{15}$ là:

A. $\frac{4}{0}$

B. $4$

C. $\frac{4}{5}$

D. $\frac{4}{15}$

Câu 3: Kết quả của phép tính $\frac{2}{3}+\frac{1}{5}$ là:

A. $\frac{3}{8}$

B. $\frac{1}{4}$

C. $\frac{13}{15}$

D. $\frac{2}{15}$

Câu 4: Tính rồi rút gọn: $\frac{17}{20}-\frac{1}{4}$

A. $1$

B. $\frac{12}{20}$

C. $\frac{3}{4}$

D. $\frac{3}{5}$

Câu 5: Thực hiện phép tính: $\frac{9}{25}+2$

A. $\frac{18}{25}$

B. $\frac{59}{25}$

C. $\frac{9}{27}$

D. $\frac{11}{25}$

Câu 6: Thực hiện phép tính: $3-\frac{5}{14}$

A. $\frac{5}{7}$

B. $\frac{77}{42}$

C. $\frac{37}{14}$

D. $\frac{47}{14}$

Câu 7: Thực hiện phép tính: $\frac{5}{3}-\frac{1}{8}+\frac{3}{4}$

A.$\frac{55}{24}$

B. $\frac{19}{24}$

C. $\frac{5}{8}$

D. $\frac{7}{8}$

Câu 8: Một hình chữ nhật có chiều dài $\frac{4}{5}\mathrm{m}$, chiều rộng kém chiều dài $\frac{1}{2}\mathrm{m}$. Vậy nửa chu vi hình chữ nhật đó là:

A. $\frac{3}{10}\mathrm{m}$

B. $\frac{11}{10}\mathrm{m}$

C. $\frac{11}{5}\mathrm{m}$

D. $\frac{21}{10}\mathrm{m}$

II. Bài tập tự luận

Câu 1: Thực hiện các phép tính sau (rút gọn kết quả nếu có thể):

$\begin{array}{l}\mathrm{a})\frac{5}{9}+\frac{2}{9}\\ \mathrm{b})\frac{3}{5}+\frac{3}{7}\\ \mathrm{c})\frac{7}{15}-\frac{2}{5}\\ \mathrm{d})6-\frac{5}{7}\\ \mathrm{e})\frac{2}{3}-\frac{1}{12}+\frac{3}{4}\\ \mathrm{f})\frac{11}{3}-2-\frac{1}{5}\end{array}$

Câu 2: Tìm x biết:

$\begin{array}{l} \mathrm{a})\frac{4}{7}+\mathrm{x}=\frac{5}{8}\\ \mathrm{b})\mathrm{x}-\frac{2}{9}=\frac{28}{45}\\ \mathrm{c})\mathrm{x}-\frac{1}{5}=\frac{11}{12}-\frac{2}{3}\\ \mathrm{d})\frac{2}{5}+\mathrm{x}=2-\frac{3}{4}\end{array}$

Câu 3: Điền dấu thích hợp vào chỗ chấm:

$$\begin{gathered} \mathrm{a})\frac{3}{4}-\frac{1}{2}\cdot \cdot \cdot \frac{1}{6} \\ \mathrm{b})\frac{3}{8}+\frac{2}{5}\cdot \cdot \cdot \frac{1}{4}+\frac{9}{20} \\ \mathrm{c})\frac{5}{4}+\frac{1}{2}-1\cdot \cdot \cdot \frac{3}{4}-\frac{2}{15}+\frac{9}{30}\hspace{0.17em} \end{gathered}$$

Câu 4: Một vòi nước giờ thứ nhất chảy được $\frac{1}{3}$ bể nước, giờ thứ hai chảy được nhiều hơn giờ thứ nhất $\frac{1}{8}$ bể nước . Tính số phần bể chưa có nước  sau hai giờ vòi nước đó chảy vào bể.

Câu 5: Tính bằng cách thuận tiện:

$\frac{1}{10}+\frac{4}{20}+\frac{9}{30}+\frac{16}{40}+\frac{25}{50}+\frac{36}{60}+\frac{49}{70}+\frac{64}{80}+\frac{81}{90}$

Câu 6: Giá trị của x thỏa mãn  là:

Có 

Câu 8: Một cửa hàng buổi sáng bán được  tổng số mét vải, buổi chiều bán được nhiều hơn buổi sáng  tổng số mét vải. Hỏi số mét vải còn lại chiếm bao nhiêu phần tổng số mét vải của cửa hàng đó?

III. Bài tập vận dụng

Câu 1: Tính:

Câu 2: Tính bằng cách thuận tiện nhất:

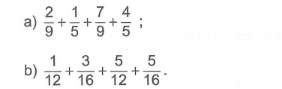
Câu 3: Khoanh vào chữ đặt trước câu trả lời đúng:

Cho:

Số thích hợp để viết vào ô trống là:

A. 1

B. 2

C. 3

D. 4

Câu 4: Khoanh vào chữ đặt trước câu trả lời đúng:

Câu 5: Một chai đựng nước mắm cân nặng 5/6 kg. Vỏ chai cân nặng 1/4 kg.

Hỏi:

Lượng nước trong chai cân nặng bao nhiêu ki-lô-gam?

Câu 6: Bạn Hà ngày đầu đọc được 2/3 quyển sách, ngày thứ hai đọc được 1/3 quyển sách.

Hỏi:

Còn bao nhiêu phần quyển sách bạn Hà chưa đọc?

B. Lý thuyết Ôn tập: Phép cộng và phép trừ hai phân số

1. Cộng, trừ các phân số cùng mẫu số

Quy tắc: Muốn cộng (hoặc trừ) hai phân số cùng mẫu số ta cộng (hoặc trừ) hai tử số với nhau và giữ nguyên mẫu số.

Ví dụ 1:

$$\begin{gathered} \frac{2}{9}+\frac{5}{9}=\frac{2+5}{9}=\frac{7}{9} \\ \frac{13}{15}-\frac{7}{15}=\frac{13-7}{15}=\frac{6}{15}=\frac{2}{5} \end{gathered}$$

Lưu ý: Sau khi làm phép tính cộng (hoặc trừ) hai phân số, nếu thu được phân số chưa tối giản thì ta phải rút gọn thành phân số tối giản.

2. Cộng, trừ các phân số khác mẫu số

Quy tắc: Muốn cộng (hoặc trừ) hai phân số khác mẫu số ta quy đồng mẫu số hai phân số đó rồi cộng (hoặc trừ) hai phân số đã quy đồng.

Ví dụ 1:

$\begin{array}{l}\frac{2}{3}+\frac{3}{4}=\frac{8}{12}+\frac{9}{12}=\frac{8+9}{12}=\frac{17}{12}\\ \frac{5}{6}-\frac{3}{5}=\frac{25}{30}-\frac{18}{30}=\frac{25-18}{30}=\frac{7}{30}\end{array}$

3. Tính chất của phép cộng phân số

+) Tính chất giao hoán: Khi đổi chỗ các phân số trong một tổng thì tổng của chúng không thay đổi.

+ Tính chất kết hợp: Khi cộng một tổng hai phân số với phân số thứ ba thì ta có thể cộng phân số thứ nhất với tổng của hai phân số còn lại.

+ Cộng với số 0: Phân số nào cộng với 0 cũng bằng chính phân số đó.

Lưu ý: ta thường áp dụng các tính chất của phép cộng phân số trong các bài tính nhanh.

4. Một số dạng bài tập

a) Tính giá trị các biểu thức:

Phương pháp giải: Áp dụng các quy tắc tính giá trị biểu thức như ưu tiên tính trong ngoặc trước, nhân, chia trước, cộng trừ sau …

Ví dụ: Tính giá trị biểu thức: $\frac{3}{4}-\frac{1}{7}+\frac{5}{6}$

Phương pháp: Biểu thức này chỉ chứa phép cộng và phép trừ nên ta tính lần lượt từ trái qua phải.

Cách giải: 

$$\begin{gathered} \frac{3}{4}-\frac{1}{7}+\frac{5}{6} \\ =\frac{21}{28}-\frac{4}{28}+\frac{5}{6} \\ =\frac{17}{28}+\frac{5}{6}=\frac{51}{84}+\frac{70}{84} \\ =\frac{121}{84} \end{gathered}$$

b) Tìm x

Phương pháp giải: Xác định xem x đóng vai trò số hạng chưa biết, số trừ hay số bị trừ, từ đó tìm được x.

Ví dụ: Tìm x biết:

a)$x+\frac{3}{5}=\frac{9}{10}$

b) $4-x=\frac{5}{6}$

Giải

a) 

$\begin{array}{l}x+\frac{3}{5}=\frac{9}{10}\\ x=\frac{9}{10}-\frac{3}{5}\\ x=\frac{3}{10}\end{array}$

b) 

$\begin{array}{l}4-x=\frac{5}{6}\\ x=4-\frac{5}{6}\\ x=\frac{24}{6}-\frac{5}{6}\\ x=\frac{19}{6}\end{array}$

c) Tính nhanh

Phương pháp giải: áp dụng các tính chất của phép cộng phân số để tính tổng hoặc hiệu của các phân số một cách dễ dàng hơn.

Ví dụ: Tính nhanh: $\frac{5}{9}+\frac{13}{15}+\frac{4}{9}+\frac{2}{15}$

Bài giải 

$$\begin{gathered} \frac{5}{9}+\frac{13}{15}+\frac{4}{9}+\frac{2}{15} \\ =\left(\frac{5}{9}+\frac{4}{9}\right)+\left(\frac{13}{15}+\frac{2}{15}\right) \\ =\frac{9}{9}+\frac{15}{15}=1+1=2 \end{gathered}$$

d) Toán có lời văn

Ví dụ: Một hình chữ nhật có chiều dài là 14/5 cm, chiều rộng là 4/3 cm. Tính nửa chu vi hình chữ nhật đó.

Cách giải: 

Nửa chu vi hình chữ nhật đó là:         

$\frac{14}{5}+\frac{4}{3}=\frac{62}{15}\left(cm\right)$

Đáp số: $\frac{62}{15}\left(cm\right)$