Tailieumoi.vn xin giới thiệu Bài tập Toán 11 Chương 3 Bài 2: Dãy số. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 2: Dãy số. Mời các bạn đón xem:
Bài tập Toán 11 Chương 3 Bài 2: Dãy số
A. Bài tập Dãy số
I. Bài tập trắc nghiệm
Bài 1: Chứng minh bằng phương pháp quy nạp n3 + 11n chia hết cho 6.
Bài 2: Tìm công thức tính số hạng tổng quát un theo n của dãy số sau
A. un = n2 - 3n + 10
B. un = 2n
C. un = 2n
D. un = n + 2
Vậy (*) đúng với n = k + 1. Kết luận (*) đúng với mọi số nguyên dương n.
Chọn đáp án B
Bài 3: Xét tính tăng giảm của dãy số (un) biết:
A. Dãy số giảm.
B. Dãy số không tăng không giảm
C. Dãy số không đổi.
D. Dãy số tăng
Chọn đáp án D
Bài 4: Cho dãy số . Tìm mệnh đề đúng?
A. Dãy số tăng và bị chặn.
B. Dãy số giảm và bị chặn.
C. Dãy số tăng và bị chặn dưới
D. Dãy số giảm và bị chặn trên.
Chọn đáp án A
Bài 5: Xét tính bị chặn của dãy số (un) biết:
A. Dãy số bị chặn trên
B. Dãy số bị chặn dưới.
C. Dãy số bị chặn
D. Tất cả sai.
Chọn đáp án C
Bài 6: Cho dãy số (un) xác định bởi 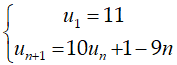
A. un = 100 + 2n
B.un = 10n + n
C. un = 100n – n2
D. Đáp án khác
Chọn đáp án B
Bài 7: Xét tính tăng giảm của dãy số (un) với
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng, không giảm
D. Dãy số không đổi.
Chọn đáp án A
Bài 8: Cho dãy số (un) biết . Mệnh đề nào sau đây đúng?
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng, không giảm
D. Dãy số là dãy hữu hạn
Chọn đáp án A
Bài 9: Cho dãy số (un) biết . Mệnh đề nào sau đây đúng ?
A. Dãy số bị chặn dưới.
B. Dãy số bị chặn trên.
C. Dãy số bị chặn.
D. Không bị chặn
Chọn đáp án C
Bài 10: Xét tính tăng, giảm và bị chặn của dãy số (un), biết:
A. Dãy số tăng, bị chặn
B. Dãy số giảm, bị chặn
C. Dãy số không tăng không giảm, không bị chặn
D. Cả A, B, C đều sai
Chọn đáp án A
Bài 11: Cho dãy số (un) được xác định như sau: . Tìm số hạng u11.
A. .
B. u11 = 4.
C. .
D. u11 = 5.
Lời giải:
Ta có:
Chọn đáp án D
Bài 12: Cho dãy số (un) được xác định như sau: . Tìm số hạng u8.
A. u8 = 3050.
B. u8 = 5003.
C. u8 = 3500.
D. u8 = 3005.
Lời giải:
Ta có:
u3 = 2u2 + 3u1 + 5 = 12
u4 = 2u3 + 3u2 + 5 = 35
u5 = 2u4 + 3u3 + 5 = 111
u6 = 2u5 + 3u4 + 5 = 332
u7 = 2u6 + 3u5 + 5 = 1002
u8 = 2u7 + 3u6 + 5 = 3005
Chọn đáp án D
II. Bài tập tự luận có lời giải
Bài 1: Chứng minh rằng với mọi số nguyên n, ta có:
Vậy (1) đúng với n = k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.
Bài 2: Với mỗi số nguyên dương n, gọi un = 9n - 1. Chứng minh rằng với mọi số nguyên dương n thì un luôn chia hết cho 8.
* Ta có u1 = 9.1 - 1 = 8 chia hết cho 8 (đúng với n = 1).
* Giả sử uk = 9k - 1 chia hết cho 8.
Ta cần chứng minh uk + 1 = 9k + 1 - 1 chia hết cho 8.
Thật vậy, ta có:
uk + 1 = 9k + 1 - 1 = 9.9k - 1 = 9(9k - 1) + 8 = 9uk + 8.
Vì 9uk và 8 đều chia hết cho 8, nên uk + 1 cũng chia hết cho 8.
Vậy với mọi số nguyên dương n thì un chia hết cho 8.
Bài 3: Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta luôn có: 2n + 1 > 2n + 3 (*)
* Với n = 2 ta có 2.2+1 > 2.2 + 3 ⇔ 8 > 7 (đúng).
Vậy (*) đúng với n = 2 .
* Giả sử với n = k, k ≥ 2 thì (*) đúng, có nghĩa ta có: 2k + 1 > 2k + 3 (1).
* Ta phải chứng minh (*) đúng với n = k + 1, có nghĩa ta phải chứng minh:
2k + 2 > 2(k + 1) + 3
Thật vậy, nhân hai vế của (1) với 2 ta được:
2.2k + 1 > 2(2k + 3) ⇔ 2k + 2 > 4k + 6 > 2k + 5.
(vì 4k + 6 > 4k + 5 > 2k + 5)
Hay 2k + 2 > 2(k + 1)+ 3
Vậy (*) đúng với n = k + 1.
Do đó theo nguyên lí quy nạp, (*) đúng với mọi số nguyên dương n ≥ 3 .
Bài 4: Tìm công thức tính số hạng tổng quát un theo n của dãy số sau
Bài 5: Xét tính tăng giảm của dãy số (un) biết:
Chọn đáp án B
Bài 6: Xét tính tăng hay giảm và bị chặn của dãy số :
Lời giải:
Chọn đáp án C
Bài 7: Cho dãy số (un) có số hạng tổng quát . Số là số hạng thứ mấy?
Lời giải:
Bài 8: Chứng minh bằng quy nạp:
Vậy (1) đúng khi n= k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.
Bài 9:
Chứng minh rằng với n ∈ N*, ta có các đẳng thức:
a. (1)
b. (2)
c. (3)
Lời giải:
a. Với n = 1, ta có:
VT = 3 – 1 = 2
VP =
Vậy VT = VP (1) đúng với n = 1
Giả thiết (1) đúng với n = k ≥ 1 nghĩa là:
(1a)
Ta chứng minh (1a) đúng với n = k + 1 nghĩa là chứng minh:
(1) đúng với n = k +1, vậy (1a) đúng với
b.
Với n = 1 thì
Vậy (2) đúng với n = 1
Giả sử đẳng thức đúng với n = k, tức là:
Khi đó ta chứng minh (2) đúng với n = k +1
Ta có :
(2) đúng với n = k + 1. Vậy nó đúng với mọi n ∈ N*
c. (3)
Khi n = 1 vế trái bằng 1
Vậy (3) đúng với n = 1
Giả sử đẳng thức (3) đúng với n = k nghĩa là:
(3a)
Ta phải chứng minh (3a) đúng khi n = k + 1
+ Ta cộng 2 vế của (3) cho (k + 1)2
Vậy đẳng thức đúng với n = k + 1. Do đó, đẳng thức đúng với mọi n ∈ N*
Bài 10 Chứng minh rằng với n ∈ N*
a. n3 + 3n2 + 5n chia hết cho 3.
b. chia hết cho 9
c. n3 + 11n chia hết cho 6.
Lời giải:
Đặt An =
+ Ta có: với n = 1
chia hết 3
+ Giả sử với n = k ≥ 1 ta có:
chia hết 3 (giả thiết quy nạp)
+ Ta chứng minh chia hết 3
Thật vậy, ta có:
Theo giả thiết quy nạp chia hết 3, hơn nữa 9(k + 1) chia hết 3
Nên = n3 + 3n2 + 5n chia hết cho 3 với mọi ∀n ∈ N*
b. 4n + 15n – 1 chia hết cho 9
Đặt
với n = 1 => = 4 + 15 – 1 = 18 chia hết 9
+ Giả sử với n = k ≥ 1 ta có:
chia hết 9 (giả thiết quy nạp)
+ Ta chứng minh: chia hết 9
Thật vậy, ta có:
Ak+1 = (4k+1 + 15(k + 1) – 1) = 4k.41 + 15k + 15 – 1
= (4k + 15k – 1) + (3.4k + 15) = Ak + 3(4k + 5)
Theo giả thiết quy nạp chia hết 9, hơn nữa:
3(4k + 5) chia hết 9 ( chứng minh tương tự) ∀k ≥ 1 nên chia hết 9
Vậy An = 4n + 15n – 1 chia hết cho 9 ∀n ∈ N*
c. n3 + 11n chia hết cho 6.
Đặt Un = n3 + 11n
+ Với n = 1 => U1 = 12 chia hết 6
+ Giả sử với n = k ≥ 1 ta có:
chia hết 6 (giả thiết quy nạp)
Ta chứng minh: Uk+1 chia hết 6
Thật vậy ta có:
Uk+1 = (k + 1)3 + 11(k +1) =
+ Theo giả thiết quy nạp thì:
chia hết 6, hơn nữa
chia hết 6 ∀k ≥ 1 (2 số liên tiếp nhân với nhau chia hết cho 2)
Do đó: Uk+1 chia hết 6
Vậy: Un = n3 + 11n chia hết cho 6 ∀n ∈ N*
Bài 11: Cho dãy số (un) được xác định bởi . Viết năm số hạng đầu của dãy.
Lời giải:
Ta có năm số hạng đầu của dãy
Vậy năm số hạng đầu của dãy là: .
III. Bài tập vận dụng
Bài 1 Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta có các bất đẳng thức:
a. 3n > 3n + 1
b. 2n+1 > 2n + 3
Bài 2 Cho tổng với
a. Tính S1, S2, S3
b. Dự đoán công thức tính tổng Sn và chứng minh bằng quy nạp.
Bài 3 Chứng minh rằng số đường chéo của một đa giác lồi n cạnh là
Bài 4 Chứng minh rằng với n Є N*, ta có đẳng thức:
a) 2 + 5+ 8+.... + 3n - 1 = ;
b) ;
c) 12 + 22 + 32 +….+ n2 = .
Bài 5 Chứng minh rằng với n ε N* ta luôn có:
a) n3 + 3n2 + 5n chia hết cho 3;
b) 4n + 15n - 1 chia hết cho 9;
c) n3 + 11n chia hết cho 6.
Bài 6 Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta có các bất đẳng thức:
a) 3n > 3n + 1;
b) 2n + 1 > 2n + 3
Bài 7

a) Tính S1, S2, S3.
b) Dự đoán công thức tính tổng Sn và chứng minh bằng quy nạp.
Bài 8 Tìm công thức tính số hạng tổng quát un theo n của dãy số sau
Bài 9 Xét tính tăng giảm của dãy số (un) biết:
Bài 10 Cho dãy số 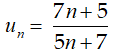
B. Lý thuyết Dãy số
I. Định nghĩa.
1. Định nghĩa dãy số.
Mỗi hàm số u xác định trên tập các số nguyên dương được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu:
Người ta thường viết dãy số dưới dạng khai triển: u1, u2, u3,…,un,..,
Trong đó, un = u(n) hoặc viết tắt là (un), và gọi u1 là số hạng đầu, un là số hạng thứ n và là số hạng tổng quát của dãy số.
- Ví dụ 1:
a) Dãy các số tự nhiên chẵn: 2; 4; 6; 8; …có số hạng đầu u1 = 2, số hạng tổng quát là un = 2n.
b) Dãy các số tự nhiên chia hết cho 5 là 5; 10; 15; 20; … có số hạng đầu u1 = 5, số hạng tổng quát là un = 5n.
2. Định nghĩa dãy số hữu hạn.
- Mỗi hàm số u xác định trên tập M = {1, 2, 3,.., m} với được gọi là một dãy số hữu hạn.
- Dạng khai triển của nó là u1, u2, u3,…, um, trong đó u1 là số hạng đầu, um là số hạng cuối.
- Ví dụ 2.
a) 4, 7, 10, 13, 16, 19 là dãy số hữu hạn có u1 = 4; u6 = 19.
b) là dãy số hữu hạn có u1 = 4; u6 = .
II. Cách cho một dãy số.
1. Dãy số cho bằng công thức của số hạng tổng quát
- Ví dụ 3.
a) Cho dãy số (un) với un = n2. (1)
Từ công thức (1), ta có thể xác định được bất kì một số hạng nào của dãy số. Chẳng hạn, u10 = 102 = 100.
Nếu viết dãy số này dưới dạng khai triển ta được:
1, 4, 9, 16, 25, 36,…, n2,….
b) Dãy số (un) với có dạng khai triển là:
2. Dãy số cho bằng phương pháp mô tả
Ví dụ 4. Số là số thập phân vô hạn không tuần hoàn
Nếu lập dãy số (un) với un là giá trị gần đúng thiếu của số với sai số tuyệt đối 10-n thì:
u1 = 1,4 ; u2 = 1,41; u3 = 1,414; u4 = 1,4142,….
Đó là dãy số được cho bằng phương pháp mô tả, trong đó chỉ ra cách viết các số hạng liên tiếp của dãy.
3. Dãy số cho bằng phương pháp truy hồi
Cho một dãy số bằng phương pháp truy hồi, tức là:
a) Cho số hạng đầu (hay vài số hạng đầu).
b) Cho hệ thức truy hồi, tức là hệ thức biểu thị số hạng thứ n qua số hạng (hay vài số hạng) đứng trước nó.
- Ví dụ 5. Dãy số (un) được xác định như sau:
Dãy số như trên là dãy số cho bằng phương pháp truy hồi.
III. Biểu diễn hình học của dãy số.
Vì dãy số là một hàm số trên nên ta có thể biểu diễn dãy số bằng đồ thị. Khi đó trong mặt phẳng tọa độ, dãy số được biểu diễn bằng các điểm có tọa độ (n ; un).
Ví dụ 6: Dãy số (un) với có biểu diễn hình học như sau:
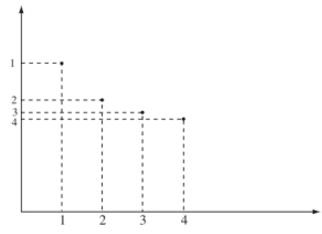
IV. Dãy số tăng, dãy số giảm và dãy số bị chặn
1. Dãy số tăng, dãy số giảm.
- Định nghĩa 1:
Dãy số (un) được gọi là dãy số tăng nếu ta có un +1 > un với mọi .
Dãy số (un) được gọi là dãy số giảm nếu ta có un +1 < un với mọi .
- Ví dụ 7. Dãy số (un) với un = 2 – 2n là dãy số giảm.
Thật vậy, với mọi xét hiệu un +1 – un. Ta có:
un +1 – un = 2 – 2(n + 1) – (2 – 2n) = – 2 < 0
Do un +1 – un < 0 nên un +1 < un với mọi
Vậy dãy số đã cho là dãy số giảm.
- Chú ý:
Không phải mọi dãy số đều tăng hoặc giảm. Chẳng hạn dãy số (un) với un = (– 1)n tức là dãy: – 1, 1, – 1, 1, – 1, 1, – 1…không tăng cũng không giảm.
2. Dãy số bị chặn.
- Dãy số (un) được gọi là bị chặn trên nếu tồn tại một số M sao cho:
- Dãy số (un) được gọi là bị chặn dưới nếu tồn tại một số m sao cho:
- Dãy số (un) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m; M sao cho:
- Ví dụ 8. Dãy số (un) với bị chặn vì 0 < un ≤ 1.a