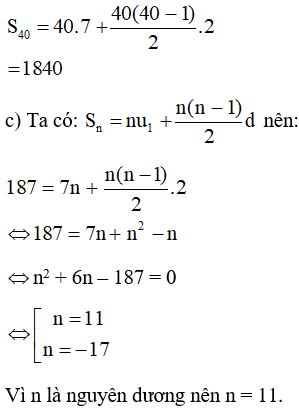Tailieumoi.vn xin giới thiệu Bài tập Toán 11 Chương 3 Bài 3: Cấp số cộng. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 3: Cấp số cộng. Mời các bạn đón xem:
Bài tập Toán 11 Chương 3 Bài 3: Cấp số cộng
A. Bài tập Cấp số cộng
I. Bài tập trắc nghiệm
Bài 1: Cho hai cấp số cộng (un): 4, 7, 10, 13, 16, ...và (vn):1, 6, 11, 16, 21, ...Hỏi trong 100 số hạng đầu tiên của mỗi cấp số cộng , có bao nhiêu số hạng chung?
A.10
B. 20
C. 30
D. 40
Ứng với 20 giá trị của t cho 20 giá trị của n và 20 giá trị của k.
Vậy có 20 số hạng chung của hai dãy
Chọn đáp án B
Bài 2: Cho cấp số cộng (un) thỏa mãn: 
a. Tính số hạng thứ 100 của cấp số ;
A. - 243
B. - 295
C. - 231
D. - 294
b. Tính tổng 15 số hạng đầu của cấp số ;
A. - 244
B. - 274
C. - 253
D. - 285
Chọn đáp án B
Chọn đáp án D
Bài 3: Ba số hạng liên tiếp của một cấp số cộng có tổng bằng -9 và tổng các bình phương của chúng bằng 29. Tìm số hạng đầu tiên
A. -3 hoặc – 6
B. – 4 hoặc -2
C. -1 hoặc -5
D. -4 hoặc - 7
Chọn đáp án B
Bài 4: Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có góc nhỏ nhất bằng 25°. Tìm 2 góc còn lại?
A. 65° ; 90°.
B. 75° ; 80°.
C. 60° ; 95°.
D. 55°; 100°.
Chọn đáp án C
Bài 5: Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?
A. a2 + c2 = 2ab + 2bc.
B. a2 - c2 = 2ab - 2bc.
C. a2 + c2 = 2ab - 2bc.
D. a2 - c2 = ab - bc.
Chọn đáp án B
Bài 6: Tìm x để 3 số : 1 - x; x2 ; x + 1 theo thứ tự lập thành một cấp số cộng?
A. Không có giá trị nào của x.
B. x = ± 2 .
C. x = ± 1 .
D. x = 0
Chọn đáp án B
Bài 7: Dãy số (un) có phải là cấp số cộng không ? Nếu phải hãy xác định số công sai d, biết rẳng
a. un = 2n + 3
A. d = -2
B. d = 3
C. d = 5
D. d = 2
b. un = -3n + 1
A. d = -2
B. d = 3
C. d = -3
D. d = 1
c. un = n2 + 1
A. d = Ø
B. d = 3
C. d = -3
D. d = 1
d. un =
A. d = Ø
B. d =
C. d = -3
D. d = 1
Bài 8: Cho cấp số cộng có 8 số hạng. Số hạng đầu bằng 3 số hạng cuối bằng 24. Tính tổng các số hạng này
A. 105
B. 27
C. 108
D. 111
Chọn đáp án C
Bài 9: Cho một cấp số cộng có u1 = -3; u6 = 27. Tìm d ?
A. d = 5
B. d = 7
C. d = 6
D. d = 8
Chọn đáp án C
Bài 10: Cho 4 số lập thành cấp số cộng. Tổng của chúng bằng 22. Tổng các bình phương của chúng bằng 166. Tổng các lập phương của chúng bằng :
A. 22
B. 166
C. 1752
D. 1408
Chọn đáp án D
Bài 11: Cho các dãy số sau, dãy số nào là cấp số cộng
Lời giải:
Đáp án: B
Dãy ở câu b là CSC với công sai d = - 3.
Bài 12: Cho 4 số lập phương thành cấp số cộng. Tổng của chúng bằng 22. Tổng các bình phương của chúng bằng 166. Tổng các lập phương của chúng bằng :
A. 22 B. 166 C. 1752 D. 1408
Lời giải:
Đáp án: D
Gọi 4 số lập thành cấp số cộng là u1,u2,u3,u4
Vậy 4 số đó là 1,4,7,10 hoặc 10,7,4,1
Tổng các lập phương của chúng: 13+43+73+103=1408
Bài 13: Trong mặt phẳng toạ độ, cho đồ thị (d) của hàm số y= 4x-5.
Với mỗi số nguyên dương, gọi An là giao điểm của(d) và đường thẳng x=n. Xét dãy số (un) với un là tung độ của điểm An. Tính u1+...+u15.
A. 405 B. 305 C. 205 D. 105
Lời giải:
Đáp án: A
Dễ thấy un = 4n -5
Ta có: un+1 = 4(n + 1) - 5 = 4n - 1
⇒ un+1=un+4 với n ≥ 1 ⇒ (un) là một cấp số cộng với công sai d = 4
II. Bài tập tự luận có lời giải
Bài 1: Cho cấp số cộng (un) có: u1 = -0,1; d = 0,1. Số hạng thứ 7 của cấp số cộng này là:
Lời giải:
Bài 2: Cho cấp số cộng (un) thỏa:
a. Xác định công thức tổng quát của cấp số
b. Tính S = u1 + u4 + u7 +...+ u2011.
Bài 3: Cho dãy số (un) có d = –2; S8 = 72. Tính u1 ?
Lời giải:
Bài 4: Cho dãy số (un) có u1 = -1; d = 2; Sn = 483 Tính số các số hạng của cấp số cộng?
Lời giải:
Bài 5: Bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120. Tính tổng của hai số hạng đầu tiên?
Lời giải:
Bài 6: Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?
Lời giải:
Bài 7: Tìm x biết x2 + 1, x - 2, 1 - 3x lập thành cấp số cộng ;
Lời giải:
Bài 8: Tìm m để phương trình x3 - 3x2 - 9x + m = 0 có ba nghiệm phân biệt lập thành cấp số cộng.
Lời giải:
Bài 9: Phương trình x4 - 2(m + 1)x2 + 2m + 1 = 0 (1) có bốn nghiệm phân biệt lập thành cấp số cộng.
Lời giải:
Bài 10: Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành một cấp số cộng. Độ dài các cạnh của tam giác đó là:
Lời giải:
Ba cạnh a, b, c ( a < b < c) của một tam giác theo thứ tự đó lập thành một cấp số cộng thỏa mãn yêu cầu thì:
III. Bài tập vận dụng
Bài 1: Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế. Hỏi rạp hát có tất cả bao nhiêu ghế?
Bài 2 Cho các dãy số (un) sau :
Hỏi có bao nhiêu dãy số là cấp số cộng ?
Bài 3 Viết ba số xen giữa các số 2 và 22 để được cấp số cộng có 5 số hạng. Tính tổng của ba số viết xen giữa đó ?
Bài 4 Cho tứ giác ABCD biết 4 góc của tứ giác lập thành một cấp số cộng và góc A bằng 30°. Tìm công sai d ?
Bài 5 Cho cấp số cộng (un) thỏa mãn
Bài 6 Trong các dãy số sau đây, dãy số nào là cấp số cộng? Tính số hạng đầu và công sai của nó:
a)
b)
c)
d)
Bài 7 Tìm số hạng đầu và công sai của các cấp số cộng sau, biết:
a) ,
b) .
Bài 8 Trong các bài toán về cấp số cộng, ta thường gặp năm đại lượng .
a) Hãy viết các hệ thức liên hệ giữa các đại lượng để có thể tìm được các đại lượng còn lại?
b) Lập bảng theo mẫu sau và điền vào chỗ trống thích hợp:

Bài 9 Mặt sàn tầng một của một ngôi nhà cao hơn mặt sân . Cầu thang đi từ tầng một lên tầng gồm bậc, mỗi bậc cao .
a) Hãy viết công thức để tìm độ cao của một bậc tuỳ ý so với mặt sân.
b) Tính độ cao của sàn tầng hai so với mặt sân.
Bài 10 Từ giờ đến giờ trưa, đồng hồ đánh bao nhiêu tiếng, nếu nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ
B. Lý thuyết Cấp số cộng
I. Định nghĩa.
- Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ sai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
Số d được gọi là công sai của cấp số cộng.
- Nếu (un) là cấp số cộng với công sai d, ta có công thức truy hồi:
un+1 = un + d với (1)
- Đặc biệt, khi d = 0 thì cấp số cộng là một dãy số không đổi (tất cả các số hạng đều bằng nhau).
- Ví dụ 1. Dãy số hữu hạn: 1, 4, 7, 10, 13, 16, 19 là một cấp số cộng với số hạng đầu u1 = 1; công sai d = 3.
II. Số hạng tổng quát
- Định lí: Nếu cấp số cộng (un) có số hạng đầu u1 và công sai d thì số hạng tổng quát un được xác định bởi công thức:
un = u1 + (n – 1)d với n ≥ 2.
- Ví dụ 2. Cho cấp số cộng (un), biết u1 = 1; d =5.
a) Tìm u10.
b) Số 106 là số hạng thứ bao nhiêu?
Lời giải:
a) Số hạng thứ 10 là u10 = u1 + (10 – 1)d = 1 + 9.5 = 46.
b) Ta có: un = u1 + (n – 1)d. Vì un =106 nên:
106 = 1 + (n – 1).5
105 = (n – 1).5
21 = n – 1 nên n = 22.
Vậy 106 là số hạng thứ 22.
III. Tính chất các số hạng của cấp số cộng.
- Định lí 2:
Trong một cấp số cộng, mỗi số hạng (trừ số hạng đầu và số cuối) đều là trung bình cộng của hai số đứng kề với nó, nghĩa là:
IV. Tổng n số hạng đầu của một cấp số cộng
- Định lí: Cho cấp số cộng (un). Đặt Sn = u1 + u2 + u3 + … + un.
Khi đó: .
- Chú ý: vì un = u1 + (n – 1)d nên ta có: .
Ví dụ 3. Cho cấp số cộng (un) với un = 2n + 5.
a) Tìm u1 và d.
b) Tính tổng 40 số hạng đầu tiên.
c) Biết Sn = 187, tìm n.
Lời giải:
a) Ta có: u1 = 2.1 + 5 = 7; u2 = 2.2 + 5 = 9.
Suy ra, d = u2 – u1 = 2.
b) Tổng 40 số hạng đầu tiên là: