Đáp án: C

Giải thích:

Các số 0; $\frac{1}{3}$ 1 đều là các số hữu tỉ nên là số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn.

Do đó A, B và D là sai.

Số $\sqrt{7}$ là số thập phân vô hạn không tuần hoàn.

Đáp án: D

Giải thích:

Ta có:

• |x| = x khi x > 0;

• |x| = –x khi x < 0;

• |x| = 0 khi x = 0.

Đáp án: B

Giải thích:

Số đối của số $\sqrt{5}$ là số $-\sqrt{5}$

Đáp án: D

Giải thích:

Ta có độ chính xác d = 0,0005 là số phần chục nghìn nên ta sẽ làm tròn số đến hàng phần nghìn.

Đáp án: B

Giải thích:

Ta có: |0,155 – 0,2| = |–0,045| = 0,045 < 0,05

Vì 0,05 là số phần trăm nên số 0,155 đến hàng phần mười để được số 0,2.

Đáp án: B

Giải thích:

Ta có:

• $\frac{1}{3}$; 0 và $\frac{2}{3}$ là các số hữu tỉ.

• $\sqrt{2}=1,\mathrm{414...}$ là một số vô tỉ.

Đáp án: D

Giải thích:

Gạch dưới chữ số hàng nghìn của số đã cho: 982 555.

Nhìn chữ số ngay bên phải chữ số 2 là chữ số 5 ở hàng trăm.

Ta thấy 5 = 5  nên tăng thêm một đơn vị vào chữ số 2 và thay các chữ số bên phải bằng số 0 ta được số 983 000.

Vậy số 982 555 làm tròn đến hàng nghìn ta được 983 000.

Đáp án: B

Giải thích:

Tất cả các số tự nhiên, số nguyên, số hữu tỉ, số vô tỉ đều là số thực.

Do đó $\frac{2}{3}\in \mathrm{ℝ}$ và $\sqrt{3}\in \mathrm{ℝ}.$

Nên $\sqrt{3}\notin \mathrm{ℝ}$ là sai.

Đáp án: B

Giải thích:

Vì 25 > 0  và 25² = 625 nên $\sqrt{625}=25$.

Đáp án: A

Giải thích:

Ta có: $\sqrt{6^2}=\left|6\right|=6.$

Đáp án: B

Giải thích:

Ta có: |x – 1| = 5

Suy ra $\left[\begin{array}{l}\mathrm{x}-1=5\\ \mathrm{x}-1=-5\end{array}\right.$

Do đó $\left[\begin{array}{l}\mathrm{x}=6\\ \mathrm{x}=-4\end{array}\right.$

Vậy có 2 số thực x thỏa mãn |x – 1| = 5.

Đáp án: A

Giải thích:

Làm tròn đến hàng đơn vị các số ta được:

4,87 ≈ 5; 2,8 ≈ 3; 2,3 ≈ 2; 1,9 ≈ 2.

Khi đó ta có ước lượng phép tính: $\frac{4,87+2,8}{2,3+1,9}\approx \frac{5+3}{2+2}=\frac{8}{4}=2.$

Do đó $\frac{4,87+2,8}{2,3+1,9}\approx 2.$

Vậy ước lượng kết quả của phép tính $\frac{4,87+2,8}{2,3+1,9}$ ta được kết quả là 2.

Đáp án: A

Giải thích:

• Ta có a = 3333, làm tròn số đến hàng chục ta được x = 3330.

Ta có |a – x| = |3333 – 3330| = |3| = 3.

Mà 2 < 3 < 6 nên 2 < |a – x| < 6.

Do đó A và C là sai.

• Ta có:

x – 5 = 3330 – 5 = 3325;

x + 5 = 3330 + 5 = 3335.

Nên suy ra : x – 5 ≤ a ≤ x + 5.

Do đó A đúng.

Đáp án: A

Giải thích:

Ta có: $0<\sqrt{3}=1,\mathrm{732...}<\frac{5}{2}=2.5$

Do đó trên trục số:

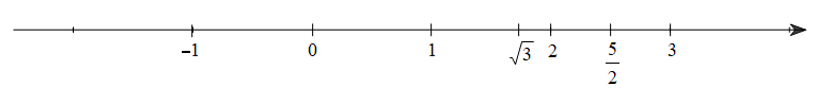
• Điểm $\sqrt{3}$ nằm bên trái điểm $\frac{5}{2}$. Do đó A đúng và B sai.

• Điểm $\sqrt{3}$ nằm bên phải điểm 0. Do đó C sai.

• Điểm 0 nằm bên trái điểm $\frac{5}{2}$. Do đó D sai.

Đáp án: D

Giải thích:

• Ta có –0,6 <  0 nên |–0,6| = –(–0,6) = 0,6. Do đó phương án B sai.

• Vì –0,7 <  0 nên |–0,7| = –(–0,7) = 0,7.

Vì 0,6 < 0,7 nên |–0,6| < |–0,7|. Do đó phương án A sai.

• Vì $\sqrt{0,7}$  và $-\sqrt{0,7}$ là hai số đối nhau nên $\left|\sqrt{0,7}\right|=\left|-\sqrt{0,7}\right|$.

Do đó phương án C sai.

• Vì $-\frac{2}{3}<0$ nên $\left|-\frac{2}{3}\right|=-\left(-\frac{2}{3}\right)=\frac{2}{3};$

Vì $\frac{1}{3}>0$ nên $\left|\frac{1}{3}\right|=\frac{1}{3};$ 

Vì $\frac{2}{3}>\frac{1}{3}$ nên $\left|-\frac{2}{3}\right|>\left|\frac{1}{3}\right|$. Do đó phương án D đúng.

Đáp án: B

Giải thích:

Ta có: 1,(02) = 1,020202…

Làm tròn số 1,020202…với độ chính xác 0,005 tức là ta làm tròn số đó đến hàng phần trăm.

Vì chữ số hàng phần nghìn của 1,020202…là 0 < 5 nên 1,020202… ≈ 1,02.

Vậy làm tròn số 1,(02) với độ chính xác 0,005 ta được số 1,02.

Đáp án: C

Giải thích:

Ta có: $|3,5\left|-\right|-1,5|+\sqrt{3^2}=3,5-1,5+3=5$

Đáp án: D

Giải thích:

Làm tròn các số đến hàng đơn vị ta được:

5,2 ≈ 5 và 4,1 ≈ 4.

Khi đó: (5,2)². (4,1)² ≈ 5².4² = 25. 16 = 400.

Đáp án: A

Giải thích:

Trên trục số, điểm O biểu diễn gốc 0, điểm A biểu diễn số 3; điểm B biểu diễn số $\sqrt{10};$ điểm C biểu diễn số 4.

Ta có $\sqrt{10}=3,\mathrm{16227766...}$ làm tròn với độ chính xác 0,5 tức là làm tròn đến hàng đơn vị. Khi đó ta có 3,16227766 ≈ 3.

Vậy số $\sqrt{10}$ khi được làm tròn với độ chính xác 0,5 thì sẽ được biểu diễn bởi điểm A trên trục số.

Đáp án: A

Giải thích:

Ta có:

• $\sqrt{\frac{81}{169}}=\sqrt{\frac{9^2}{{13}^2}}=\sqrt{{\frac{9}{13}}^2}=\frac{9}{13}$ 

Do đó A đúng, B và D là sai.

• $\sqrt{\frac{81}{169}}=\frac{9}{13}$ là một số hữu tỉ suy ra C sai.

Đáp án: B

Giải thích:

Ta có: $\sqrt{|-16|}=\sqrt{16}=4$

Đáp án: B

Giải thích:

Ta có $\sqrt{0,16}-\sqrt{0,09}$

$=\sqrt{0,4^2}-\sqrt{0,3^2}$ 

= 0,4 – 0,3

= 0,1.

Đáp án: B

Giải thích:

Ta có:

• $\sqrt{100}=\sqrt{{10}^2}=10;$ 

• $\sqrt{64}+\sqrt{36}=\sqrt{8^2}+\sqrt{6^2}=8+6=14.$ 

Vì 10 < 14 nên $\sqrt{100}<\sqrt{64}+\sqrt{36}$ 

Do đó $\sqrt{64+36}<\sqrt{64}+\sqrt{36}$ 

Vậy bạn An sai từ bước (2).

Đáp án: B

Giải thích:

Ta có $\mathrm{a}=\sqrt{4.25}=\sqrt{100}=\sqrt{{10}^2}=10$;

$\mathrm{b}=\sqrt{4}.\sqrt{25}=\sqrt{2^2}.\sqrt{5^2}=2.5=10.$

Vì 10 = 10 nên $\sqrt{4.25}=\sqrt{4}.\sqrt{25}$

Do đó a = b.

Vậy a = b.

Đáp án: C

Giải thích:

Ta có: |29 675 – 30 000| = |–325| = 325 < 500

Vì 500 là số trăm nên người đó đã làm tròn đến hàng nghìn.

Vậy người đó đã làm tròn giá xăng đến hàng nghìn.

Đáp án: A

Giải thích:

Do độ chính xác đến hàng trăm nên ta làm tròn số 98 984 322 đến hàng nghìn và được kết quả là 98 984 000.

Vậy làm tròn với độ chính xác d = 300 ta được dân số Việt Nam khoảng 98 984 nghìn người.

Đáp án: B

Giải thích:

Ta có: (x – 1)² ≥ 0 với mọi x

Nên $\sqrt{{\left(\mathrm{x}-1\right)}^2}\ge 0$ với mọi x.

Do đó $-\sqrt{{\left(\mathrm{x}-1\right)}^2}\le 0$ với mọi x.

Suy ra $5-\sqrt{{\left(\mathrm{x}-1\right)}^2}\le 5$ với mọi x.

Hay A ≤ 5 với mọi x.

Dấu “=” xảy ra khi và chỉ khi (x – 1)² = 0

Tức là x – 1 = 0 hay x = 1.

Vậy A_min = 5 khi x = 1.

Đáp án: D

Giải thích:

Điểm trung bình Toán cả năm của An là:

${\mathrm{ĐTB}}_{\mathrm{mcn}}=\frac{8,5+2.8,9}{3}=8,\mathrm{766666...}$

Làm tròn kết quả đến chữ số thập phân thứ nhất ta được 8,8.

Đáp án: B

Giải thích:

Ta có:

$\mathrm{A}=\sqrt{{\left(\sqrt{3}-1\right)}^2}-\sqrt{{\left(1-\sqrt{3}\right)}^2}$

$=\left|\sqrt{3}-1\right|-\left|1-\sqrt{3}\right|$

Ta có: $\sqrt{3}=1,732050808$ > 1

Nên $\sqrt{3}-1>0$ và $1-\sqrt{3}<0$ 

Do đó: $\left|\sqrt{3}-1\right|=\sqrt{3}-1$ và $\left|1-\sqrt{3}\right|=\sqrt{3}-1.$

Khi đó $\mathrm{A}=\left(\sqrt{3}-1\right)-\left(\sqrt{3}-1\right)=0$

Đáp án: C

Giải thích:

Ta có:

7,5 – 3.|5 – 2x| = –4,5

3.|5 – 2x| = 7,5 –(–4,5)

3.|5 – 2x| = 7,5 + 4,5

3.|5 – 2x| = 12

|5 – 2x| = 12 : 3

|5 – 2x| = 4

Trường hợp 1: 5 – 2x = 4

2x = 5 – 4

2x = 1

$\mathrm{x}=\frac{1}{2}$ 

Trường hợp 2: 5 – 2x = –4

2x = 5 – (–4)

2x = 5 + 4

2x = 9

x = 9 : 2

$\mathrm{x}=\frac{9}{2}$ 

Vậy có hai giá trị của x thoả mãn là $\mathrm{x}=\frac{1}{2}$; $\mathrm{x}=\frac{9}{2}$.

Xem thêm các bài trắc nghiệm Toán 7 Chân trời sáng tạo hay, chi tiết khác:

Trắc nghiệm Bài 3. Làm tròn và ước lượng kết quả

Trắc nghiệm Ôn tập chương 2

Trắc nghiệm Bài 1. Hình hộp chữ nhật – Hình lập phương

Trắc nghiệm Bài 2. Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

Trắc nghiệm Bài 3. Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác