Với tóm tắt lý thuyết Toán lớp 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 7.

Lý thuyết Toán lớp 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

A. Lý thuyết Cộng, trừ, nhân, chia số hữu tỉ

1. Cộng và trừ hai số hữu tỉ

Mọi số hữu tỉ đều viết được dưới dạng phân số với mẫu dương nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.

Ví dụ 1: Tính:

a) $\frac{-6}{18}+\frac{18}{27};$

b) – 0,32 + 0,98;

c) – 5 + $2\frac{1}{5}$.

Hướng dẫn giải

a) $\frac{-6}{18}+\frac{18}{27}=\frac{-1}{3}+\frac{2}{3}=\frac{-1+2}{3}=\frac{1}{3};$

b) – 0,32 + 0,98 = 0,98 – 0,32 = 0,66;

c) – 5 + $2\frac{1}{5}$ = $-\frac{25}{5}+\frac{11}{5}=\frac{-25+11}{5}=\frac{-14}{5}.$

Chú ý:

• Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc cộng và trừ đối với số thập phân.

• Trong phép cộng trừ với số hữu tỉ $\mathrm{\mathbb{Q}}$, ta có thể áp dụng các tính chất giao hoán, kết hợp, quy tắc dấu ngoặc như trong phép cộng trừ với số nguyên $\mathrm{\mathbb{Z}}$.

• Đối với một tổng trong $\mathrm{\mathbb{Q}}$, ta có thể đổi chỗ các số hạng, đặt dấu ngoặc để nhóm các số hạng một cách tùy ý như các tổng trong $\mathrm{\mathbb{Z}}$.

• Hai số đối nhau luôn có tổng bằng 0:

a + (– a) = 0.

Ví dụ 2: Thực hiện phép tính

a) $\frac{2}{-3}+\frac{-5}{6}+\frac{1}{3}+1\frac{1}{6}$;

b) $\frac{31}{3}-\frac{1}{2}-\left(\frac{2}{3}-\frac{1}{2}\right)$.

Hướng dẫn giải

a) $\frac{2}{-3}+\frac{-5}{6}+\frac{1}{3}+1\frac{1}{6}$

$=\frac{-2}{3}+\frac{-5}{6}+\frac{1}{3}+\frac{7}{6}$  (Viết số hữu tỉ dưới dạng phân số có mẫu dương)

$=\frac{-2}{3}+\frac{1}{3}+\frac{-5}{6}+\frac{7}{6}$             (Tính chất giao hoán)

$=\left(\frac{-2}{3}+\frac{1}{3}\right)+\left(\frac{-5}{6}+\frac{7}{6}\right)$      (Tính chất kết hợp)

$=\frac{-1}{3}+\frac{2}{6}$

$=\frac{-1}{3}+\frac{1}{3}=0$                       (Tổng hai số đối nhau bằng 0)

b)  $\frac{31}{3}-\frac{1}{2}-\left(\frac{2}{3}-\frac{1}{2}\right)$

$=\frac{31}{3}-\frac{1}{2}-\frac{2}{3}+\frac{1}{2}$                  (Quy tắc bỏ dấu ngoặc có dấu “–” đằng trước)

$=\left(\frac{31}{3}-\frac{2}{3}\right)+\left(-\frac{1}{2}+\frac{1}{2}\right)$         (Quy tắc đặt dấu ngoặc có dấu “+” đằng trước)

$=\frac{29}{3}+0=\frac{29}{3}$                       (Cộng với số 0)

2. Nhân và chia hai số hữu tỉ

• Ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

Chú ý:

• Phép nhân các số hữu tỉ cũng có các tính chất của phép nhân phân số.

• Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc nhân và chia đối với số thập phân.

Ví dụ 1: Tính:

a) $\frac{23}{3}\cdot \frac{6}{46}\cdot \left(-\frac{9}{10}\right)$;

b) $-\frac{7}{6}:1\frac{5}{7}$;

c) $\frac{7}{6}\cdot 3\frac{1}{4}+\frac{7}{6}\cdot \left(-0,25\right)$.

Hướng dẫn giải

a) $\frac{23}{3}\cdot \frac{6}{46}\cdot \left(-\frac{9}{10}\right)$

$=\frac{23}{3}\cdot \frac{3}{23}\cdot \left(-\frac{9}{10}\right)$

$=1\cdot \left(-\frac{9}{10}\right)=-\frac{9}{10}$                (Nhân với số 1)

b) $-\frac{7}{6}:1\frac{5}{7}$

$=-\frac{7}{6}:\frac{12}{7}$

$=-\frac{7}{6}\cdot \frac{7}{12}=-\frac{49}{72}$

c) $\frac{7}{6}\cdot 3\frac{1}{4}+\frac{7}{6}\cdot \left(-0,25\right)$

$=\frac{7}{6}\cdot \left[3\frac{1}{4}+\left(-0,25\right)\right]$

$=\frac{7}{6}\cdot \left(\frac{13}{4}+\frac{-1}{4}\right)$

$=\frac{7}{6}\cdot \frac{12}{4}=\frac{7}{2}$

Ví dụ 2: 1,25 . (– 4,6) = – (1,25 . 4,6) = – 5,75.

B. Bài tập tự luyện

B1. Bài tập tự luận

Bài 1. Tính giá trị của các biểu thức sau:

a) $\left(7+3\frac{1}{4}-\frac{3}{5}\right)+\left(0,4-5\right)-\left(4\frac{1}{4}-1\right)$;

b) $\frac{2}{3}-\left[\left(-\frac{7}{4}\right)-\left(\frac{1}{2}+\frac{3}{8}\right)\right]$;

c) $\left(9-\frac{1}{2}-\frac{3}{4}\right):\left(7-\frac{1}{4}-\frac{5}{8}\right)$;

d) $3-\frac{1-\frac{1}{7}}{1+\frac{1}{7}}$.

Hướng dẫn giải

a) $\left(7+3\frac{1}{4}-\frac{3}{5}\right)+\left(0,4-5\right)-\left(4\frac{1}{4}-1\right)$

$=7+3\frac{1}{4}-\frac{3}{5}+0,4-5-4\frac{1}{4}+1$

$=\left(7-5+1\right)+\left(3\frac{1}{4}-4\frac{1}{4}\right)+\left(-\frac{3}{5}+0,4\right)$

$=3+\left(-1\right)+\left(-0,6+0,4\right)$

$=2+\left(-0,2\right)=1,8$

b) $\frac{2}{3}-\left[\left(-\frac{7}{4}\right)-\left(\frac{1}{2}+\frac{3}{8}\right)\right]$

$=\frac{2}{3}-\left[\left(-\frac{7}{4}\right)-\left(\frac{4}{8}+\frac{3}{8}\right)\right]$

$=\frac{2}{3}-\left[\left(-\frac{14}{8}\right)-\frac{7}{8}\right]$

$=\frac{2}{3}-\left(-\frac{21}{8}\right)$

$=\frac{2}{3}+\frac{21}{8}$

$=\frac{16}{24}+\frac{63}{24}=\frac{79}{24}$

c) $\left(9-\frac{1}{2}-\frac{3}{4}\right):\left(7-\frac{1}{4}-\frac{5}{8}\right)$

$=\left(\frac{36}{4}-\frac{2}{4}-\frac{3}{4}\right):\left(\frac{56}{8}-\frac{2}{8}-\frac{5}{8}\right)$

$=\frac{31}{4}:\frac{49}{8}=\frac{31}{4}\cdot \frac{8}{49}=\frac{62}{49}$

d) $\left(1+\frac{1}{7}\right)=3-\frac{6}{7}:\frac{8}{7}=3-\frac{6}{7}\cdot \frac{7}{8}=3-\frac{3}{4}=\frac{12}{4}-\frac{3}{4}=\frac{9}{4}$.

Bài 2. Tính:

a) $\frac{-8}{18}+\frac{15}{27}$;

b) $3,5-\left(-\frac{2}{7}\right)$;

c) $-0,25\cdot \left(-0,4\right)$;

d) $-6:3\frac{1}{5}$.

Hướng dẫn giải

a) $\frac{-8}{18}+\frac{15}{27}=\frac{-4}{9}+\frac{5}{9}=\frac{1}{9}$;

b) $3,5-\left(-\frac{2}{7}\right)=\frac{7}{2}+\frac{2}{7}=\frac{49}{14}+\frac{4}{14}=\frac{53}{14}$;

c) $-0,25\cdot \left(-0,4\right)=0,25\cdot 0,4=0,1$

d) $-6:3\frac{1}{5}=-6:\frac{16}{5}=-6\cdot \frac{5}{16}=\frac{-15}{8}$.

B2. Bài tập trắc nghiệm

Bài 3. Giá trị của biểu thức $\frac{3}{5}-\left(\frac{1}{2}-\frac{2}{5}\right)$ là

A. $\frac{-3}{10}$;

B. $\frac{1}{2}$;

C. $\frac{3}{2}$;

D. $\frac{7}{10}$.

Hướng dẫn giải

Đáp án đúng là: B

$\frac{3}{5}-\left(\frac{1}{2}-\frac{2}{5}\right)$ = $\frac{3}{5}-\frac{1}{2}+\frac{2}{5}$ = $\left(\frac{3}{5}+\frac{2}{5}\right)-\frac{1}{2}$ = $1-\frac{1}{2}$ = $\frac{1}{2}$.

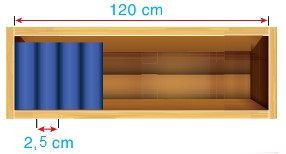
Bài 4. Ngăn đựng sách của một giá sách trong thư viện dài 120 cm (xem hình dưới). Người ta dự định xếp các cuốn sách dày khoảng 2,5 cm vào ngăn này. Hỏi ngăn sách đó có thể để được nhiều nhất bao nhiêu cuốn sách như vậy?

A. 50 cuốn sách;

B. 48 cuốn sách;

C. 40 cuốn sách;

D. 25 cuốn sách.

Hướng dẫn giải

Đáp án đúng là: B

Ngăn sách đó có thể để được nhiều nhất số cuốn sách như thế là:

120 : 2,5 = 48 (cuốn sách).

Bài 5. Giá trị của biểu thức $6,25+\left[1,75-\left(0,75-2,75\right)\right]$ là

A. 6;

B. 6,5;

C. 9,5;

D. 10.

Hướng dẫn giải

Đáp án đúng là: D

$6,25+\left[1,75-\left(0,75-2,75\right)\right]$ 

= $6,25+\left[1,75-0,75+2,75\right]$ 

= $6,25+1,75-0,75+2,7$

= $\left(6,25+2,75\right)+\left(1,75-0,75\right)$

= 9 + 1

= 10

Xem thêm các bài tóm tắt lý thuyết Toán 7 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 1: Tập hợp các số hữu tỉ

Lý thuyết Bài 3: Lũy thừa với số mũ tự nhiên của một số hữu tỉ

Lý thuyết Bài 4: Thứ tự thực hiện các phép tính. Quy tắc chuyển vế

Lý thuyết Toán 7 Chương 1: Số hữu tỉ

Lý thuyết Bài 5: Làm quen với số thập phân vô hạn tuần hoàn