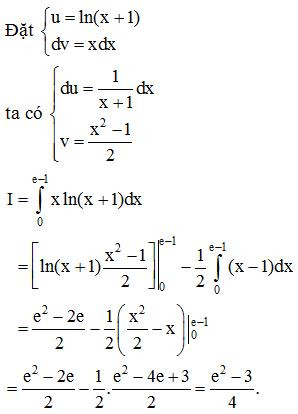Tailieumoi.vn xin giới thiệu Bài tập Toán 12 Chương 3 Bài 2: Tích phân. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 12. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 2: Tích phân. Mời các bạn đón xem:
Bài tập Toán 12 Chương 3 Bài 2: Tích phân
A. Bài tập Tích phân
I. Bài tập trắc nghiệm
Câu 1: Tích phân
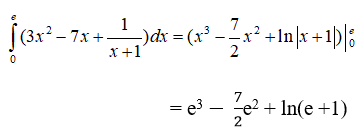
Ta chọn đáp án A
Câu 2: Cho hai tích phân:
Trong các khẳng định sau , khẳng định nào đúng?
Đặt t = - x ⇒ dt = -dx Khi x = a thì t = - a , khi x = - a thì t = a
Ta có:
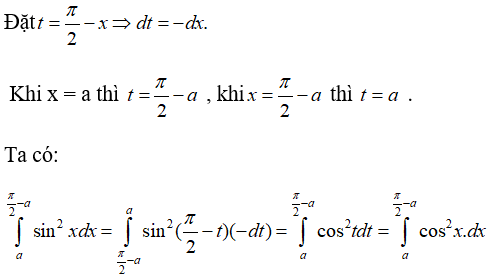
Vậy chọn đáp án B.
Câu 3:
Đặt: t = 3 - x ⇒ dt = - dx .
Khi x = 0 thì t = 3, khi x = a thì t = 3-a.
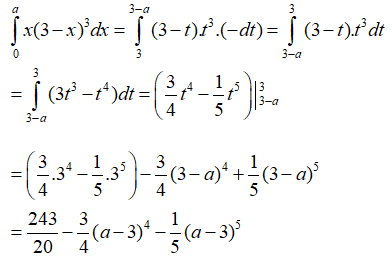
Vậy chọn đáp án B.
Câu 4: Tính tích phân
A. I = 0
B. I = a2
C. I = -a2
D. I = 2a2 .
Ta có:
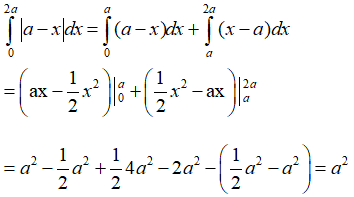
Vậy chọn đáp án B.
Câu 5: Tính tích phân 
Đặt t = lnx ⇒ dt = ()dx . Khi x = 1 thì t = 0, khi x = 2e thì t = 1+ln2. Ta có:
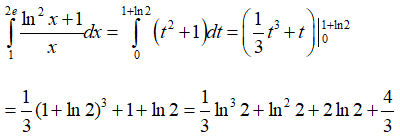
Vậy chọn đáp án D.
Câu 6: Tính tích phân
Đặt u = x và dv = cos(a - x)dx ,suy ra du = dx và v = -sin(a-x). Do đó
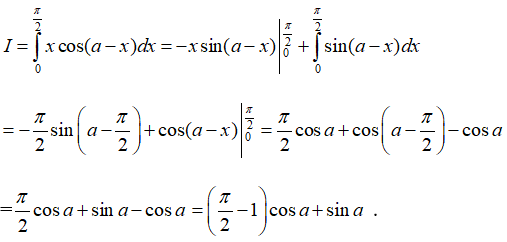
Vậy chọn đáp án C.
Câu 7:
Khẳng định nào dưới đây là sai?
Đặt u = x2 - 1 , ta có du = 2xdx. Khi x = 1 thì u = 0, x = 2 thì u = 3. Do đó
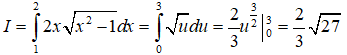
Vậy chọn đáp án C.
Câu 8:
Tìm n?
A.6
B.5
C.4
D.3
Ta có:
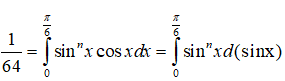
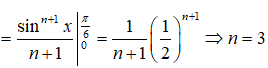
Vậy chọn đáp án D.
Câu 9: Kết quả của tích phân
được viết dưới dạng a+bln2. Tính giá trị của a+b.
Ta có:
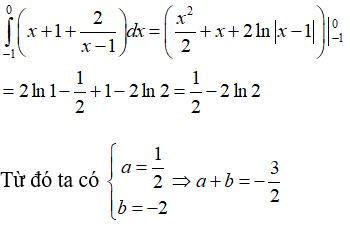
Vậy chọn đáp án D
Câu 10: Giả sử
Giá trị của K là:
A.9
B.3
C.81
D.8
Ta có:
Do đó, K = 3
II. Bài tập tự luận có lời giải
Câu 1: Cho:
Tính giá trị của a-b.
Lời giải:
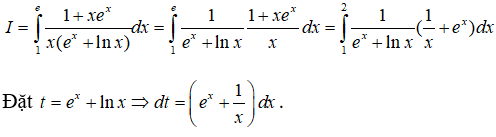
Khi x = 1 thì t = e, khi x = e thì t = ee + 1 .
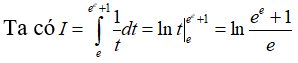
Từ đó suy ra: a = 1; b = 1 nên a – b = 0.
Câu 2: Cho
Giả sử đặt t = thì ta được:
Lời giải:
⇒(t - 2)3 = ex
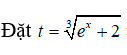
Đổi cận: x = 0 thì t = 3 ; x = 3ln2 thì t = 4
Khi đó
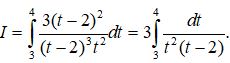
Câu 3: Cho
Khi đó a+b bằng
Lời giải:
Ta có
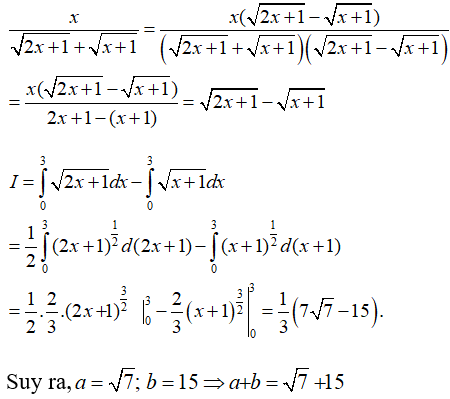
Câu 4: Cho
Đặt t = x2 . Biết
Lời giải:
Đặt t = x2 ⇒ dt = 2xdx. Ta có:
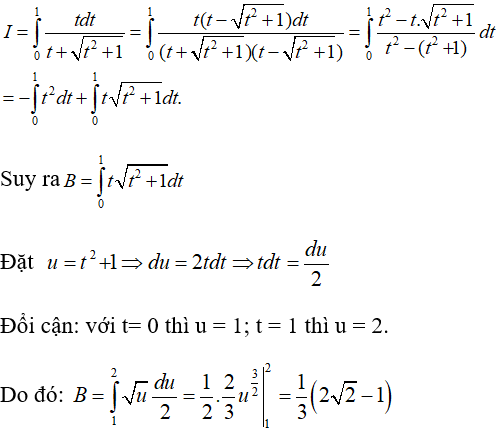
Câu 5: Nếu
với a < d < b thì
Lời giải:
Ta có:
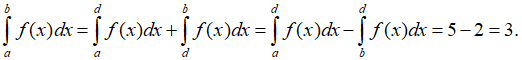
Câu 6: Cho tích phân
Nếu biến đổi số t = sin2x thì:
Lời giải:
Ta có
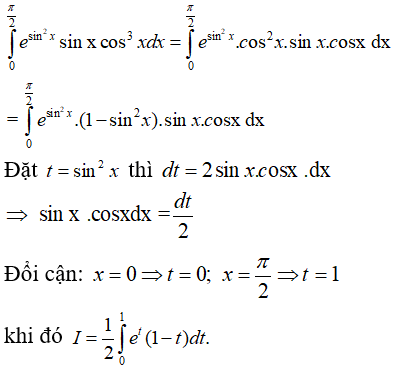
Câu 7: Tính
Lời giải:
Ta có
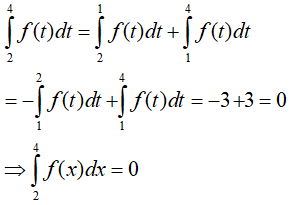
Câu 8:
Lời giải:
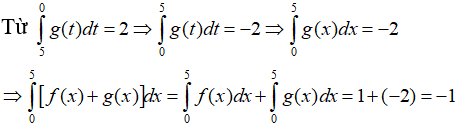
Bài 9:
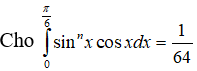
Tìm n?
Lời giải:
Ta có:
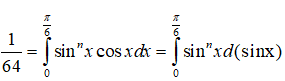
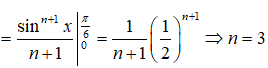
Bài 10: Kết quả của tích phân
được viết dưới dạng a+bln2. Tính giá trị của a+b.
Lời giải:
Ta có:
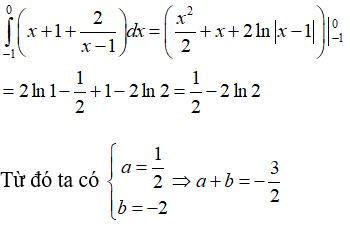
III. Bài tập vận dụng
Bài 1 Giả sử 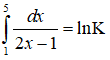Giá trị của K là?
Bài 2 Cho: 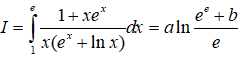Tính giá trị của a-b.
Bài 3 Cho 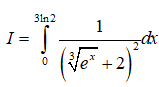Giả sử đặt t = thì ta được?
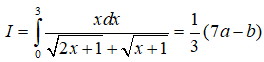
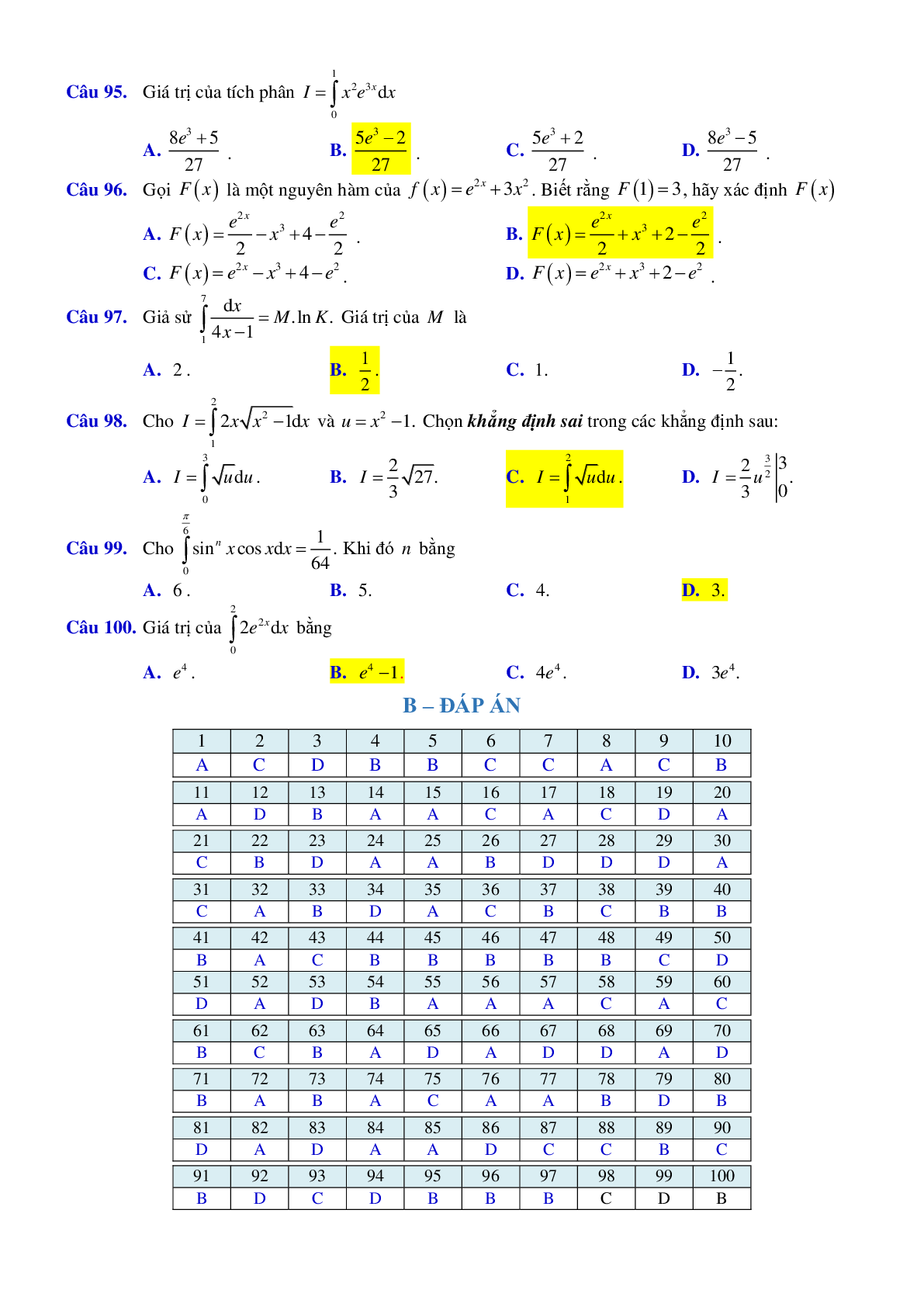
Bài 4 Cho. Khi đó a+b bằng?
Bài 5 Cho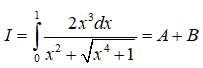 Đặt t = x2 . Biết 
Bài 6 Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = (x -1)e2x ,trục tung và đường thẳng y = 0. Tính thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục Ox
Bài 7 Cho tích phân 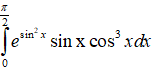. Nếu biến đổi số t = sin2x thì:
Bài 8 Tính tích phân
Bài 9 Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a, x = b (a < b) quanh trục Ox.
Bài 10 Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x3 - x và đồ thị hàm số y = x - x2.
B. Lý thuyết Tích phân
I. Khái niệm tích phân
1. Diện tích hình thang cong
- Cho hàm số y = f(x) liên tục, không đổi dấu trên đoạn [a; b]. Hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được gọi là hình thang cong.
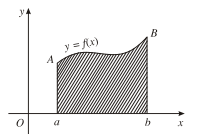
- Ta xét bài toán tìm diện tích hình thang cong bất kì:
Cho hình thang cong giới hạn bởi các đường thẳng x = a; x = b (a < b); trục hoành và đường cong y = f(x), trong đó f(x) là hàm số liên tục, không âm trên đoạn [a; b].
Với mỗi , kí hiệu S(x) là diện tích của phần hình thang cong đó nằm giữa hai đường thẳng vuông góc với Ox lần lượt tại a và b.
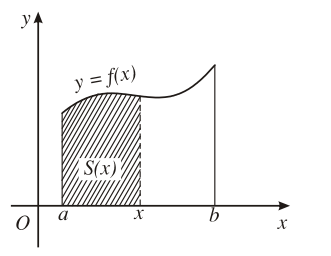
Ta chứng minh được S(x) là một nguyên hàm của f(x) trên đoạn [a; b].
Giả sử F(x) cũng là một nguyên hàm của f(x) thì có một hằng số C sao cho S(x) = F(x) + C.
Vì S(a) = 0 nên F(a) + C = 0 hay C = – F(a).
Vậy S(x) = F(x) – F(a).
Thay x = b vào đẳng thức trên, ta có diện tích của hình thang cần tìm là:
S(b) = F(b) – F(a).
2. Định nghĩa tích phân
Cho f(x) là hàm số liên tục trên đoạn [a; b]. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a; b].
Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a; b]) của hàm số f(x), kí hiệu
Ta còn dùng kí hiệu để chỉ hiệu số F(b) – F(a).
Vậy
Ta gọi là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.
- Chú ý.
Trong trường hợp a = b hoặc a > b, ta quy ước:
Ví dụ 1.
a)
b)
- Nhận xét.
a) Tích phân của hàm số f từ a đến b có thể kí hiệu là hay . Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào biến x hay t.
b) Ý nghĩa hình học của tích phân.
Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b] thì tích phân là diện tích S của hình thang cong giới hạn bởi đồ thị của f(x), trục Ox và hai đường thẳng x = a; x = b. Vậy .
II. Tính chất của tích phân.
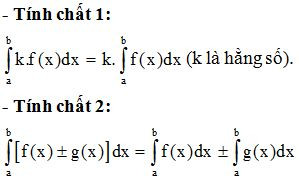
Ví dụ 2. Tính: .
Lời giải:
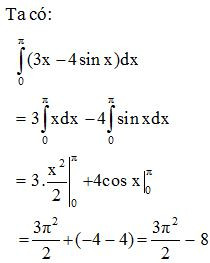
- Tính chất 3.
(a < c < b).
Ví dụ 3. Tính .
Lời giải:
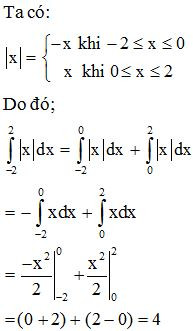
III. Phương pháp tính tích phân
1. Phương pháp đổi biến số
- Định lí:
Cho hàm số f(x) liên tục trên đoạn [a; b]. Giả sử hàm số có đạo hàm liên tục trên đoạn sao cho và .
Khi đó:
Ví dụ 4. Tính .
Lời giải:
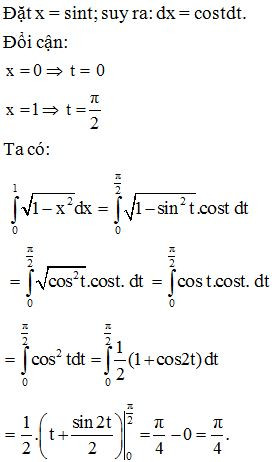
- Chú ý:
Trong nhiều trường hợp ta còn sử dụng phép đổi biến số ở dạng sau:
Cho hàm số f(x) liên tục trên đoạn [a; b]. Để tính , đôi khi ta chọn hàm số u = u(x) làm biến số mới, trong đó trên đoạn [a; b], u(x) có đạo hàm liên tục và .
Giả sử có thể viết: f(x) = g(u(x)). u’(x) với với g(u) liên tục trên đoạn
Khi đó, ta có:
Ví dụ 5. Tính
Lời giải:
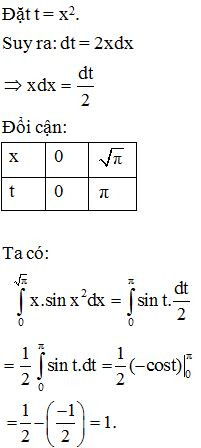
2. Phương pháp tính tích phân từng phần
- Định lí.
Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a; b] thì:
Hay
Ví dụ 6. Tính
Lời giải:
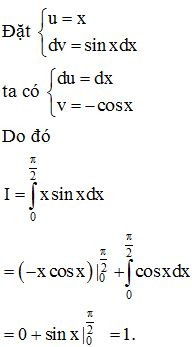
Ví dụ 7. Tính .
Lời giải:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
