Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết và bài tập ứng dụng của tích phân Toán lớp 12, tài liệu bao gồm 47 trang, tuyển chọn Lý thuyết và bài tập ứng dụng của tích phân Toán lớp 12 đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

A. LÝ THUYẾT ỨNG DỤNG CỦA TÍCH PHÂN

1. Diện tích hình phẳng

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x) liên tục trên đoạn [a ; b], trục hoành và hai đường thẳng x=a, x=b được xác định: \(S = \int_a^b | f(x)|dx\)

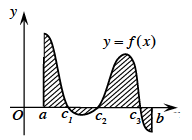
\((H)\left\{ {\begin{array}{*{20}{l}}{y = f(x)}\\{y = 0}\\{x = a}\\{x = b}\end{array}} \right.\)

\(S = \int_a^b | f(x)|dx\)

Diện tích hình phẳng giới hạn bới đồ thị hàm số y=f(x), y=g(x) liên tục trên đoạn [a ; b] và hai đường thẳng x=a, x=b được xác định: \(S = \int_a^b | f(x) - g(x)|dx\)

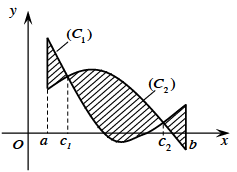
\((H)\left\{ {\begin{array}{*{20}{l}}{\left( {{C_1}} \right):y = {f_1}(x)}\\{\left( {{C_2}} \right):y = {f_2}(x)}\\{x = a}\\{x = b}\end{array}} \right.\)

\(S = \int_a^b {\left| {{f_1}(x) - {f_2}(x)} \right|} dx\)

Chú ý:

- Nếu trên đoạn [a ; b], hàm số f(x) không đổi dấu thì: \(\int_a^b | f(x)|dx = \left| {\int_a^b f (x)dx} \right|\)

- Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối

- Diện tích của hình phẳng giới hạn bởi các đường x=g(y), x=h(y) và hai đường thẳng y=c, y=d được xác định: \(S = \int_c^d | g(y) - h(y)|dy\)

2. Thể tích vật thể và thể tích khối tròn xoay

a) Thể tích vật thể:

Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x \((a \le x \le b)\). Giả sử S(x) là hàm số liên tục trên đoạn [a ; b]

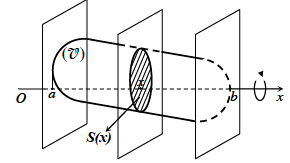
Khi đó, thể tích của vật thể B được xác định: \(V = \int_a^b S (x)dx\)

b) Thể tích khối tròn xoay:

Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y=f(x), trục hoành và hai đường thẳng x=a, x=b quanh trục Ox:

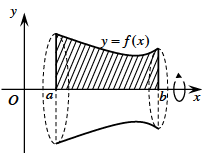
\(\left\{ {\begin{array}{*{20}{l}}{(C):y = f(x)}\\{(Ox):y = 0}\\{x = a}\\{x = b}\end{array}} \right.\)

\({V_x} = \pi \int\limits_a^b {{{\left[ {f(x)} \right]}^2}d{\rm{x}}} \)

Chú ý:

- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x=g(y), trục hoành và hai đường thẳng y=c, y=d quanh trục Oy:

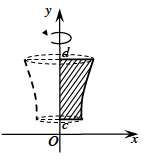
\(\left\{ {\begin{array}{*{20}{l}}{(C):y = g(y)}\\{(Oy):x = 0}\\{y = c}\\{y = d}\end{array}} \right.\)

\({V_y} = \pi \int\limits_c^d {{{\left[ {g(y)} \right]}^2}dy} \)

- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y=f(x), y=g(x) và hai đường thẳng x=a, x=b quanh trục O x :

\(V = \pi \int_a^b {\left| {{f^2}(x) - {g^2}(x)} \right|} dx\)

B. CÂU HỎI TRẮC NGHIỆM

I. Câu hỏi tính diện tích hình phẳng giới hạn bởi các đường:

Những điểm cần lưu ý:

Trường hợp 1. Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a ; b]. Diện tích hình phẳng giới hạn bởi các đường y=f(x), y=g(x), x=a, x=b là \(S = \int_a^b | f(x) - g(x)|dx\).

Phương pháp giải toán

+) Giải phương trình f(x)=g(x) (1)

+) Nếu (1) vô nghiệm thì \(S = \left| {\int_a^b {(f(} x) - g(x))dx} \right|\).

+) Nếu (1) có nghiệm thuộc [a ; b]. giả sử \(\alpha \) thì

\(S = \left| {\int_a^\alpha  {(f(} x) - g(x))dx} \right| + \left| {\int_a^b {(f(} x) - g(x))dx} \right|\)

Chú ý: Có thể lập bảng xét dấu hàm số f(x)-g(x) trên đoạn \([{\rm{a}};{\rm{b}}]\) rồi dựa vào báng xét dấu để tính tích phân.

Trường hợp 2. Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a ; b]. Diện tích hình phẳng giới hạn bởi các đường y=f(x), y=g(x) là \(S = \int_\alpha ^\beta  {\left| {f(x) - g(x)} \right|} dx\). Trong đó \(\alpha ,\beta \) là nghiệm nhỏ nhất và lớn nhất của phương trình \(f(x) = g(x)(a \le \alpha  < \beta  \le b)\).

Phương pháp giải toán:

Buớc 1. Giải phương trình f(x)=g(x) tìm các giá trị \(\alpha ,\beta \).

Buớc 2. Tính \(S = \int_\alpha ^\beta  {\left| {f(x) - g(x)} \right|} dx\) như trường hợp 1 .

BÀI TẬP

Câu 1. Công thức tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y=f(x), y=g(x) liên tục trên [a ; b] và hai đường thẳng \(x = a,x = b(a < b)\) là:

A. \(S = \pi \int_a^b {\left| {f(x) - g(x)} \right|} dx\).

B. \(S = \int_a^b {(f(} x) - g(x))dx\).

C. \(S = \int_a^b {(f(} x) - g(x){)^2}dx\).

D. \(S = \int_a^b {\left| {f(x) - g(x)} \right|} dx\).

Câu 2. Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y=f(x), liên tục trên [a ; b] trục hoành và hai đường thẳng \(x = a,x = b(a < b)\) cho bởi công thức:

A. \(S = \int_a^b {\left| {f(x)} \right|} dx.\)

B. \(S = \int_a^b f (x)dx\).

C. \(S = \pi \int_a^b {\left| {f(x)} \right|} dx\).

D. \(S = \pi \int_a^b {{f^2}} (x)dx\).

Câu 3. Diện tích hình phẳng giới hạn bởi các đường \(y = {x^3} + 11x - 6,y = 6{x^2},x = 0,x = 2\). (Đơn vị diện tích)

A. \(\frac{4}{3}\)

B. \(\frac{5}{2}\)

C. \(\frac{8}{3}\)

D. \(\frac{{18}}{{23}}\)

Câu 4. Diện tích hình phẳng giới hạn bởi \(y = {x^3},y = 4x\) là:

A. 8

B. 9

C. 12

D. 13

Câu 5. Cho hàm số y=f(x) liên tục và nhận giá trị không âm trên đoạn \(\left[ {a;b} \right]\). Diện tích hình thang cong giới hạn bởi đồ thị của y = f(x), trục hoành và hai đường thẳng x=a, x=b được tính theo công thức.

A. \(S = \int_a^b f (x)dx\)

B. \(S =  - \int_a^b f (x)dx\).

C. \(S =  - \int_a^b {{f^2}} (x)dx\).

D. \(S = \int_a^b {{f^2}} (x)dx\).

Câu 6. Diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y=f(x) liên tục trên đoạn [a ; b], trục hoành và hai đường thẳng x=a, x=b được tính theo công thức

A. \(S = \int_a^b {\left| {f(x)} \right|} dx.\)

B. \(S = \int_a^b f (x)dx\)

C. \(S = {\int_a^b {\left| {f(x)} \right|} ^2}dx\).

D. \(S = \pi \int_a^b f (x)dx\).

Câu 7. Diện tích hình phẳng được giới hạn bởi đồ thị các hàm số y=f(x), y=g(x) liên tục trên đoạn [a ; b], trục hoành và hai đường thẳng x=a, x=b được tính theo công thức

A. \(S = {\int_a^b {\left| {f(x) - g(x)} \right|} ^2}dx\)

B. \[S = \int\limits_a^b {\left[ {f(x) - g(x)} \right]} dx\].

C. \(S = \int_a^b {\left| {f(x) - g(x)} \right|} dx\).

D. \(S = \pi {\int_a^b {\left| {f(x) - g(x)} \right|} ^2}dx\).

Câu 8. Cho đồ thị hàm số y=f(x). Diện tích hình phẳng (phần tô đậm trong hình) là

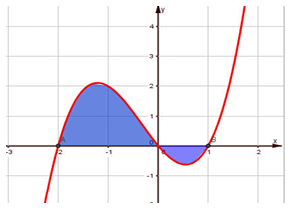
A. \(S = \int_{ - 2}^0 f (x)dx + \int_0^1 f (x)dx\)

B. \(S = \int_{ - 2}^1 f (x)dx\)

C. \(S = \int_0^{ - 2} f (x)dx + \int_0^1 f (x)dx\)

D. \(S = \int_{ - 2}^0 f (x)dx - \int_0^1 f (x)dx\)

Câu 9. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành và hai đường thẳng x=1, x=3 là

A. 19

B. 18

C. 20

D. 21

Câu 10. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = \sqrt x \), trục hoành và hai đường thẳng x=1, x=4 là

A. 4

B. \(\frac{{14}}{5}\)

C. \(\frac{{13}}{3}\)

D. \(\frac{{14}}{3}\)

Câu 11. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = \sqrt[3]{x}\), trục hoành và hai đường thẳng x=1, x=8 là

A. \(\frac{{45}}{2}\)

B. \(\frac{{45}}{4}\)

C. \(\frac{{45}}{7}\)

D. \(\frac{{45}}{8}\)

Câu 12. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y=sin x, trục hoành và hai đường thẳng \(x = \pi ,x = \frac{{3\pi }}{2}\) là

A. 1.

B. \(\frac{1}{2}\)

C. 2

D. \(\frac{3}{2}\)

Câu 13. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y=tan x, trục hoành và hai đường thẳng \(x = \frac{\pi }{6},x = \frac{\pi }{4}\) là

A. \(\ln \frac{{\sqrt 3 }}{3}\)

B. \(\ln \frac{{\sqrt 6 }}{3}\)

C. \( - \ln \frac{{\sqrt 3 }}{3}\)

D. \( - \ln \frac{{\sqrt 6 }}{3}\)

Câu 14. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {e^{2x}}\), trục hoành và hai đường thẳng x=0, x=3 là

A. \(\frac{{{e^6}}}{2} + \frac{1}{2}\)

B. \(\frac{{{e^6}}}{2} - \frac{1}{2}\)

C. \(\frac{{{e^6}}}{3} + \frac{1}{3}\)

D. \(\frac{{{e^6}}}{3} - \frac{1}{3}\)

II. Diện tích phẳng (vận dụng thấp)

Câu 15. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^3} - 3{x^2}\), trục hoành và hai đường thẳng x=1, x=4 là

A. \(\frac{{53}}{4}\)

B. \(\frac{{51}}{4}\)

C. \(\frac{{49}}{4}\)

D. \(\frac{{25}}{2}\)

Câu 16. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^4} - 3{x^2} - 4\), trục hoành và hai đường thẳng x=0, x=3 là

A. \(\frac{{142}}{5}\)

B. \(\frac{{143}}{5}\)

C. \(\frac{{144}}{5}\)

D. \(\frac{{141}}{5}\)

Câu 17. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = \frac{{x + 1}}{{x + 2}}\), trục hoành và đường thẳng x=2 là

A. 3+2 ln 2

B. 3-ln 2

C. 3-2 ln 2

D. 3+ln 2

Câu 18. Diện tích hình phẳng được giới hạn bởi parabol \(y = 2 - {x^2}\) và đường thẳng y=-x là

A. \(\frac{7}{2}\)

B. \(\frac{9}{4}\)

C. 3

D. \(\frac{9}{2}\)

Câu 19. Diện tích hình phẳng được giới hạn bới đồ thị hàm số y=cos 2 x, trục hoành và hai đường thẳng \(x = 0,x = \frac{\pi }{2}\) là

A. 2

B. 1

C. 3

D. 4

Câu 20. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^4} - 3{x^2} - 4\), trục hoành và hai đường thẳng x=0, x=3 là

A. \(\frac{{71}}{5}\)

B. \(\frac{{73}}{5}\)

C. \(\frac{{72}}{5}\)

D. 14

Câu 21. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = \frac{{x + 1}}{{x + 2}}\), trục hoành và đường thẳng x=2 là

A. 3+2 ln 2

B. 3-ln 2

C. 3-2 ln 2

D. 3+ln 2

Câu 22. Diện tích hình phẳng được giới hạn bởi parabol \(y = 2 - {x^2}\) và đường thẳng y=-x là

A. \(\frac{9}{2}\)

B. \(\frac{9}{4}\)

C. 3

D. \(\frac{7}{2}\)

Câu 23. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y=cos 2x, trục hoành và hai đường thẳng \(x = 0,x = \frac{\pi }{2}\) là

A. 1

B. 2

C. 3

D. 4