Với giải bài tập Toán lớp 6 Bài 1: Số thập phân chi tiết bám sát nội dung sgk Toán 6 Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài 1: Số thập phân
Giải SGK Toán 6
Video giải Toán 6 Bài 1: Số thập phân – Chân trời sáng tạo
A. Các câu hỏi trong bài
Giải Toán 6 trang 29 Tập 2 Chân trời sáng tạo
b) Các phân số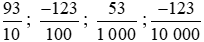 
;... có thể viết là 
;
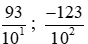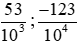;... và gọi là các phân số thập phân.
Em hãy nêu đặc điểm chung của các phân số trên.
Lời giải:
a) Phân số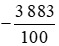
là phép chia −3 883 cho 100.
Quy tắc: Muốn chia một số cho 10; 100; 1 000 ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.
Do đó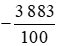
= −3 883 : 100 = −38,83.
Cách viết khác đơn giản hơn để chỉ nhiệt độ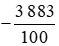
độ C là −38,83 độ C.
b) Các phân số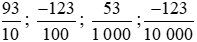 
;.… có mẫu số lần lượt là 10; 100; 1 000; 10 000;….
Ta thấy: 10 = 101; 100 = 102; 1 000 = 103; 10 000 = 104;….
Vậy đặc điểm chung của các phân số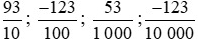 
;.… là mẫu số của các phân số này đều là lũy thừa của 10.
Giải Toán 6 trang 30 Tập 2 Chân trời sáng tạo
Thực hành 1 trang 30 Toán lớp 6 Tập 2: a) Viết các phân số thập phân sau đây dưới dạng số thập phân:
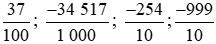
b) Viết các số thập phân sau đây dưới dạng phân số thập phân:
2; 2,5; −0,007; −3,053; −7,001; 7,01.
Lời giải:
a) Cách đổi các phân số thập phân sang số thập phân thì ta quy về bài toán chia một số cho 10; 100; 1 000 (kết quả để dưới dạng số thập phân).
Quy tắc: Muốn chia một số cho 10; 100; 1 000 ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.
Đổi lần lượt các phân số thập phân trên ra số thập phân, ta được:
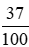= 37 : 10 = 3,7;
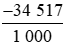= 34 517 : 1 000 = 34,517;
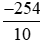= −254 : 10 = −25,4;
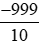= −999 : 10 = −99,9.
b)
- Các phân số thập phân được viết dưới dạng số thập phân.
- Số các chữ số thập phân bằng đúng số các chữ số 0 ở mẫu của phân số thập phân.
Đổi lần lượt các số thập phân trên ra phân số thập phân, ta được:
2 =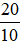 
; 2,5 = 
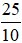; −0,007 = 
;
;
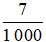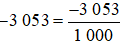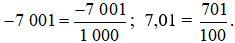
Lời giải:
a) Số đối của phân số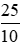 
l à phân số 
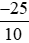, vì 
+
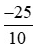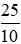= 0.
Cách đổi các phân số thập phân sang số thập phân thì ta quy về bài toán chia một số cho 10; 100; 1 000 (kết quả để dưới dạng số thập phân).
Quy tắc: Muốn chia một số cho 10; 100; 1 000 ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.
Hai số trên được viết dưới dạng số thập như sau:
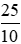= 2,5;
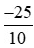= −2,5.
Thực hành 2 trang 30 Toán lớp 6 Tập 2: Tìm số đối của các số thập phân sau:
7,02; −28,12; −0,69; 0,999.
Lời giải:
Cách tìm số đối của một số thập phân: ta thêm dấu trừ vào trước số thập phân đó.
Số đối của 7,02 là −7,02.
Số đối của −28,12 là −(−28,12) hay 28,12.
Số đối của −0,69 là −(−0,69) hay 0,69.
Số đối của 0,999 là −0,999.
11,34; 9,35; −11,34; −9,35.
Lời giải:
- Các phân số thập phân được viết dưới dạng số thập phân.
- Số các chữ số thập phân bằng đúng số các chữ số 0 ở mẫu của phân số thập phân.
Đổi lần lượt các số thập phân trên ra phân số thập phân, ta được:
.
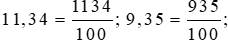
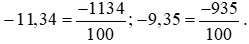
Vì −1134 < −935 < 935 < 1134 nên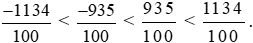
Hay −11,34 < −9,35 < 9,35 < 11,34.
Vậy các số thập phân được sắp xếp theo thứ tự từ bé đến lớn là −11,34; −9,35; 9,35; 11,34.
Giải Toán 6 trang 31 Tập 2 Chân trời sáng tạo
Thực hành 3 trang 31 Toán lớp 6 Tập 2: a) Hãy sắp xếp các số thập phân sau theo thứ tự tăng dần:
−12,13; −2,4; 0,5; −2,3; 2,4.
b) Hãy sắp xếp các số thập phân sau theo thứ tự giảm dần:
−2,9; −2,999; 2,9; 2,999.
Lời giải:
Để sắp xếp các số thập phân sau theo thứ tự tăng dần (giảm dần), ta làm như sau:
Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.
Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:
- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.
- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.
a) Sắp xếp các số thập phân sau theo thứ tự tăng dần:
* Phân loại:
- Nhóm các số thập phân dương: 0,5; 2,4.
- Nhóm các số thập phân âm: −12,13; −2,4; −2,3.
* So sánh các số thập phân trong theo nhóm:
- Nhóm các số thập phân dương: ta so sánh phần nguyên của các số trên, vì 0 < 2 nên 0,5 < 2,4.
- Nhóm các số thập phân âm:
+ Số đối của các số −12,13; −2,4; −2,3 lần lượt là 12,13; 2,4; 2,3.
+ Số 12,13 có phần nguyên là 4;
+ Hai số 2,4; 2,3 đều có phần nguyên là 2 nên ta so sánh phần thập phân của hai số.
+ Số 2,4 và 2,3 có hàng phần mười lần lượt là 4 và 3. Vì 4 > 3 nên 2,4 > 2,3.
Do đó 12,13 > 2,4 > 2,3 hay −12,13 < −2,4 < −2,3.
Từ đó ta suy ra: −12,13 < −2,4 < −2,3 < 0,5 < 2,4.
Vậy các số được sắp xếp thứ tự tăng dần là: −12,13; −2,4; −2,3; 0,5; 2,4.
b) Sắp xếp các số thập phân sau theo thứ tự giảm dần:
* Phân loại:
- Nhóm các số thập phân dương: 2,9; 2,999.
- Nhóm các số thập phân âm: −2,9; −2,999.
* So sánh các số thập phân trong theo nhóm:
- Nhóm các số thập phân dương:
+ So sánh phần nguyên: cả hai số 2,9 và 2,999 đều có phần nguyên là 2.
+ So sánh phần thập phân: Hàng phần mười của hai số đều là 9.
Ta tiếp tục so sánh hàng phần trăm: chữ số hàng phần trăm của 2,9 và 2,999 lần lượt là 0 và 9. Vì 9 > 0 nên 2,999 > 2,9.
- Nhóm các số thập phân âm:
+ Số đối của các số −2,9; −2,999 lần lượt là 2,9; 2,999.
Ở phần trên ta đã chứng minh được 2,999 > 2,9 nên −2,999 < −2,9.
Từ đó ta suy ra: 2,999 > 2,9 > −2,9 > −2,999.
Vậy các số được sắp xếp thứ tự giảm dần là: 2,999; 2,9; −2,9; −2,999.
Vận dụng trang 31 Toán lớp 6 Tập 2: Hãy sắp xếp nhiệt độ đông đặc của các chất sau từ thấp đến cao:
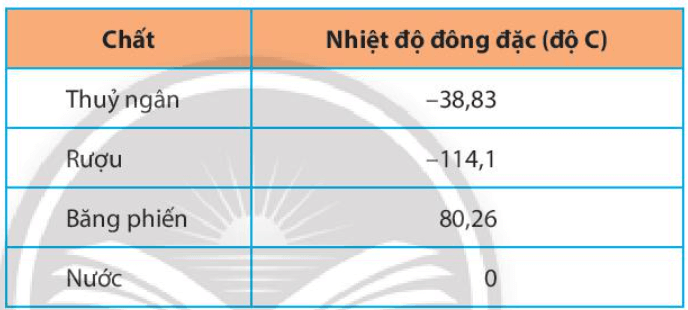
Lời giải:
Để sắp xếp nhiệt độ đông đặc của các chất sau từ thấp đến cao thì ta so sánh nhiệt độ đông đặc của của các chất rồi sắp xếp các số đó theo thứ tự tăng dần.
Sắp xếp các số thập phân: −38,83; −114,1; 80,26; 0.
* Phân loại:
- Nhóm số thập phân dương: 80,26.
- Nhóm số thập phân âm: −38,83; −114,1.
* So sánh các số thập phân trong theo nhóm:
- Nhóm số thập phân dương: chỉ có số 80,26 nên không cần phải so sánh các số trong cùng nhóm.
- Nhóm số thập phân âm:
+ Số đối của các số −38,83; −114,1 lần lượt là 38,83; 114,1.
+ Số 38,83 và 114,1 có phần nguyên lần lượt là 38 và 114. Vì 38 < 114 nên 38,83 < 114,1 (số thập phân có phần nguyên lớn hơn thì số đó lớn hơn).
Hay −38,83 > −114,1.
Do đó −114,1 < −38,83 < 0 < 80,26 (số thập phân âm nhỏ hơn số 0 và thập phân dương lơn hơn số 0).
Từ đó suy ra các số được sắp xếp thứ tự tăng dần là: −114,1; −38,83; 0; 80,26.
Vậy nhiệt độ đông đặc của các chất được sắp xếp theo tứ tự từ thấp đến cao là: Rượu: −114,1 độ C; thủy ngân: −38,83 độ C; nước: 0 độ C; băng phiến: 80,26 độ C.
B. Bài tập
Bài 1 trang 31 Toán lớp 6 Tập 2: Viết các phân số sau đây dưới dạng số thập phân:
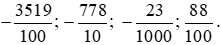
Lời giải:
a) Các phân số trên đều là phân số thập phân.
Cách đổi các phân số thập phân sang số thập phân thì ta quy về bài toán chia một số cho 10; 100; 1 000 (kết quả để dưới dạng số thập phân).
Quy tắc: Muốn chia một số cho 10; 100; 1 000 ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.
Đổi lần lượt các phân số thập phân trên ra số thập phân, ta được:
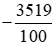= −3519 : 100 = −35,19;
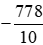= −778 : 10 = −77,8;
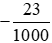= −23 : 1000 = −0,023;
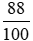= 88 : 100 = 0,88.
Bài 2 trang 31 Toán lớp 6 Tập 2: Viết các số thập phân sau đây dưới dạng phân số thập phân:
−312,5; 0,205; −10,09; −1,110.
Lời giải:
- Các phân số thập phân được viết dưới dạng số thập phân.
- Số các chữ số thập phân bằng đúng số các chữ số 0 ở mẫu của phân số thập phân.
Đổi lần lượt các số thập phân trên ra phân số thập phân, ta được:
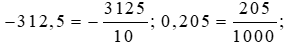
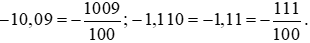
Bài 3 trang 31 Toán lớp 6 Tập 2: Tìm số đối của các số thập phân sau:
9,32; −12,34; −0,7; 3,333.
Lời giải:
Cách tìm số đối của một số thập phân: ta thêm dấu trừ vào trước số thập phân đó.
Số đối của 9,32 là −9,32;
Số đối của −12,34 là −(−12,34) hay 12,34;
Số đối của −0,7 là −(−0,7) = 0,7;
Số đối của 3,333 là −3,333.
Bài 4 trang 31 Toán lớp 6 Tập 2: Hãy sắp xếp các số thập phân sau theo thứ tự tăng dần:
−2,99; −2,9; 0,7; 1; 22,1.
Lời giải:
Để sắp xếp các số thập phân sau theo thứ tự tăng dần, ta làm như sau:
Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.
Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:
- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.
- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.
* Phân loại:
- Nhóm các số thập phân dương: 0,7; 1; 22,1.
- Nhóm các số thập phân âm: −2,99; −2,9.
* So sánh các số thập phân trong theo nhóm:
- Nhóm các số thập phân dương: ta so sánh phần nguyên của các số trên, vì 0 < 1 < 22 nên 0,7 < 1 < 22,1.
- Nhóm các số thập phân âm:
+ Số đối của các số −2,99; −2,9 lần lượt là 2,99; 2,9.
+ So sánh phần nguyên: cả hai số 2,99 và 2,9 đều có phần nguyên là 2.
+ So sánh phần thập phân: Hàng phần mười của hai số đều là 9.
Ta tiếp tục so sánh hàng phần trăm: chữ số hàng phần trăm của 2,99 và 2,9 lần lượt là 9 và 0. Vì 9 > 0 nên 2,99 > 2,9.
Do đó −2,99 < −2,9.
Từ đó ta suy ra −2,99 < −2,9 < 0,7 < 1 < 22,1.
Vậy các số được sắp xếp thứ tự tăng dần là: −2,99; −2,9; 0,7; 1; 22,1.
Bài 5 trang 31 Toán lớp 6 Tập 2: Hãy sắp xếp các số sau theo thứ tự giảm dần:
0,6;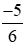
;
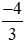; 0;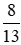 
; −1,75.
Lời giải:
Để sắp xếp các số theo thứ tự giảm dần, ta thực hiện như sau:
Bước 1: Chia thành 2 nhóm: nhóm số dương và nhóm số âm (số dương luôn lớn hơn 0 và lớn hơn số âm)
- Nhóm số dương: 0,6;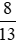 
.
- Nhóm số âm: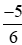 
; 
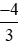; −1,75.
Bước 2: Ta so sánh các số theo nhóm với nhau:
- Nhóm số dương: 0,6;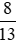 
.
Ta có: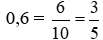 
;
Quy đồng hai phân số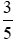 
và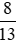 
.
Mẫu số chung: 65.
Ta thực hiện: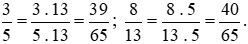 
Vì 40 > 39 nên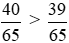 
hay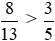 
Do đó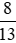 
> 0,6.
- Nhóm số âm: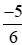 
; 
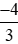; −1,75.
Ta có: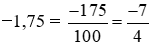 
.
Quy đồng các phân số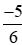 
; 
; 
.
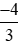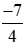Mẫu số chung: 24.
Ta thực hiện: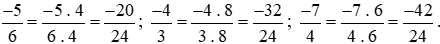
Vì −20 > −32 > −42 nên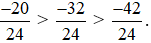 
Hay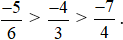 
Do đó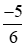 
> 
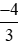> −1,75.
Từ đó suy ra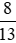 
> 0,6 > 0 >
> 
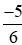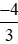> −1,75.
Vậy các số được sắp xếp theo thứ tự giảm dần là: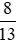 
; 0,6; 0;
; 
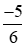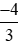; −1,75.
Xem thêm các bài giải SGK Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:
Giải SGK Toán 6 Bài tập cuối chương 5
Giải SGK Toán 6 Bài 2: Các phép tính với số thập phân
Giải SGK Toán 6 Bài 3: Làm tròn số thập phân và ước lượng kết quả
Giải SGK Toán 6 Bài 4: Tỉ số và tỉ số phần trăm
Lý thuyết Số thập phân
1. Số thập phân âm
- Phân số thập phân là phân số có mẫu số là lũy thừa của 10.
Ví dụ 1. Các phân số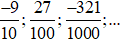 
là các phân số thập phân.
- Các phân số thập phân dương được viết dưới dạng số thập phân dương.
- Các phân số thập phân âm được viết dưới dạng số thập phân âm.
Ví dụ 2.
0,332; 12,412 là các số thập phân dương.
−3,712; −4,15 là các số thập phân âm.
Số thập phân gồm hai phần:
- Phần số nguyên viết bên trái dấu phẩy;
- Phần thập phân viết bên phải dấu phẩy.
Ví dụ 3.
- Số 42,25 là số thập phân dương có phần số nguyên là 42 và phần thập phân là 25.
- Số −12,316 là số thập phân âm có phần số nguyên là −12 và phần thập phân là 316.
2. Số đối của một số thập phân
Hai số thập phân gọi là đối nhau khi chúng biểu diễn hai phân số thập phân đối nhau.
Ví dụ 4.
- Số đối của 3,45 là −3,45;
- Số đối của −2,36 là 2,36.
3. So sánh hai số thập phân
- Nếu hai số thập phân trái dấu, số thập phân dương lớn hơn số thập phân âm.
- Trong hai số thập phân âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.
Ví dụ 5. Sắp xếp các số thập phân theo thứ tự tăng dần:
−16,25; 8,36; −21,4; 7,24.
Lời giải:
Để sắp xếp các số thập phân sau theo thứ tự tăng dần, ta thực hiện:
Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.
Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:
- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.
- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.
Sắp xếp các số thập phân sau theo thứ tự tăng dần:
* Phân loại:
- Nhóm các số thập phân dương: 8,36; 7,24.
- Nhóm các số thập phân âm: −16,25; −21,4.
* So sánh các số thập phân trong theo nhóm:
- Nhóm các số thập phân dương: ta so sánh phần nguyên của các số trên, vì 8 > 7 nên 8,36 > 7,24.
- Nhóm các số thập phân âm: Số đối của các số −16,25; −21,4 lần lượt là 16,25; 21,4.
Ta so sánh phần nguyên của hai số 16,25 và 21,4, vì 16 < 21 nên 16,25 < 21,4.
Hay −16,25 > −21,4.
Do đó −21,4 < −16,25 < 7,24 < 8,36.
Vậy các số được sắp xếp thứ tự tăng dần là: −21,4; −16,25; 7,24; 8,36.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
