Với giải bài tập Toán lớp 6 Bài 5: Bài toán về tỉ số phần trăm chi tiết bám sát nội dung sgk Toán 6 Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài 5: Bài toán về tỉ số phần trăm
Video giải Toán 6 Bài 5: Bài toán về tỉ số phần trăm – Chân trời sáng tạo
A. Các câu hỏi trong bài
Giải Toán 6 trang 45 Tập 2 Chân trời sáng tạo
Lời giải:
Vàng bốn số chín là loại vàng chứa 99,99% vàng nguyên chất nghĩa là khối lượng vàng bốn số chín chiếm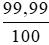
khối lượng vàng nguyên chất.
Khối lượng vàng nguyên chất có trong 100 g vàng bốn số chín là:
100 .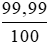 
= 
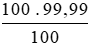= 99,99 (gam).
Vậy khối lượng vàng nguyên chất có trong 100 g vàng bốn số chín là 99,99 gam.
Thực hành 1 trang 45 Toán lớp 6 Tập 2: Tìm giá trị 25% của 200 000.
Lời giải:
Giá trị 25% của 200 000 là:
200 000 . 25% = 200 000 .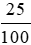 
= 50 000.
Vậy giá trị 25% của 200 000 là 50 000.
Lời giải:
Chiếc nhẫn một chỉ nặng 3,75 gam làm bằng vàng 18K, trong đó vàng 18K là hợp kim có chứa 75% vàng nguyên chất. Ta đưa bài toán này về tìm giá trị 75% của 3,75 gam.
Khối lượng vàng nguyên chất có trong một chiếc nhẫn là:
3,75 . 75% = 3,75 .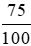 
= 
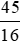= 2,8125 (gam).
Vậy khối lượng vàng nguyên chất có trong một chiếc nhẫn là 2,8125 gam.
Giải Toán 6 trang 46 Tập 2 Chân trời sáng tạo
Lời giải:
Khối lượng cafein có trong hạt cà phê Robusta của Buôn Ma Thuột là 2,5%. Khi đó, khối lượng cafein = 2,5% . khối lượng cà phê Robusta.
Do đó, khối lượng cà phê Robusta = khối lượng cafein : 2,5%.
Khối lượng cà phê Robusta để điều chế được 200 g cafein là:
200 : 2,5% = 200 :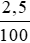 
= 200 . 
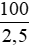= 8 000 (gam)
Vậy muốn điều chế được 200 g cafein ta cần phải có 8 000 gam hạt cà phê Robusta.
Thực hành 2 trang 46 Toán lớp 6 Tập 2: Tìm số x khi biết 12% của x là 500.
Lời giải:
12% của x là 500, số x là:
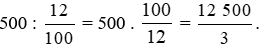
Vậy 12% của x là 500 thì x =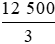 
.
b) Giá của một chiếc điện thoại sau khi đã giảm giá 25% là 800 000 đồng. Hỏi giá gốc trước khi giảm là bao nhiêu?
Lời giải:
a) Cách 1: Tính số phần trăm giá mới của chiếc ti vi so với giá gốc sau đó tính giá mới.
Giá gốc của chiếc ti vi chiếm 100% và được giảm giá 15% so với giá gốc.
Giá mới của chiếc ti vi khi giảm chiếm số phần trăm của giá gốc là:
100% − 15% = 85%
Giá mới của chiếc tivi sau khi giảm giá 15% là:
9 500 000 . 85% = 9 500 000 .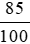 
= 8 075 000 (đồng).
Vậy giá mới của chiếc tivi sau khi giảm giá 15% là 8 075 000 đồng.
Cách 2: Tính số tiền được giảm khi mua ti vi sau đó tính giá mới của chiếc ti vi sau khi giảm.
Số tiền được giảm khi mua ti vi là:
9 500 000 . 15% = 9 500 000 .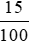 
= 1 425 000 (đồng).
Giá mới của chiếc tivi sau khi giảm giá 15% là:
9 500 000 − 1 425 000 = 8 075 000 (đồng).
Vậy giá mới của chiếc tivi sau khi giảm giá 15% là 8 075 000 đồng.
b) Giá gốc của chiếc điện thoại chiếm 100% và được giảm giá 25% so với giá gốc.
Giá của chiếc điện thoại khi giảm chiếm số phần trăm của giá gốc là:
100% − 25% = 75%
Giá gốc của chiếc điện thoại trước khi giảm là:
800 : 75% = 800 :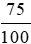 
= 800 . 
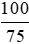≈ 1 067 000 (đồng).
Vậy giá gốc của chiếc điện thoại trước khi giảm là 1 067 000 (đồng).
Giải Toán 6 trang 47 Tập 2 Chân trời sáng tạo
a) Hỏi một năm sau Trúc nhận được tổng cộng cả vốn lẫn lãi là bao nhiêu tiền?
b) Nếu Trúc chỉ gửi tiền với lãi suất không kì hạn là 0,3% / năm và sau 40 ngày có việc cần dùng phải rút tiền ra ngay, bạn ấy sẽ nhận được tổng cộng là bao nhiêu tiền?
Lời giải:
a) 1 năm = 12 tháng.
Cách tính tiền lãi có kì hạn là:
Số tiền lãi = Số tiền gửi . lãi suất (%/năm) . số tháng gửi : 12.
Số tiền lãi sau một năm là:
10 000 000 . 6% .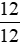 
= 10 000 000 . 
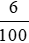= 600 000 (đồng)
Số tiền cả vốn lẫn lãi Trúc nhận được sau một năm là:
10 000 000 + 600 000 = 10 600 000 (đồng).
Vậy số tiền cả vốn lẫn lãi Trúc nhận được sau một năm là 10 600 000 đồng.
b) Cách tính tiền lãi không có kì hạn là:
Tính số tiền lãi = Số tiền gửi . lãi suất (% / năm) . số ngày thực gửi : 360.
Số tiền lãi sau 40 ngày là:
10 000 000 . 0,3% .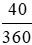 
= 10 000 000 . 
. 
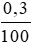≈ 3 333 (đồng).
Số tiền cả gốc lẫn lãi Trúc nhận được sau 40 ngày với lãi suất không kì hạn là 0,3% / năm là:
10 000 000 + 3 333 =10 003 333 (đồng).
Vậy nếu Trúc chỉ gửi tiền với lãi suất không kì hạn là 0,3% / năm và sau 40 ngày, Trúc nhận được tổng cộng cả gốc lẫn lãi là 10 003 333 đồng.
Lời giải:
Tỉ số phần trăm của muối trong nước biển = khối lượng muối : khối lượng nước biển . 100%.
Tỉ số phần trăm của muối trong nước biển ở Biển Chết là:
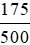. 100% = 
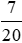. 100% = 35%.
Vậy tỉ số phần trăm của muối trong nước biển ở Biển Chết là 35%.
B. Bài tập
Giải Toán 6 trang 48 Tập 2 Chân trời sáng tạo
a) giảm giá 25%;
b) tăng giá 10%.
Lời giải:
a) Cách 1: Tính số phần trăm giá mới của quyển sách so với giá ban đầu sau đó tính giá mới.
Giá ban đầu của quyển sách chiếm 100% và được giảm giá 25% so với giá ban đầu.
Giá của quyển sách khi giảm chiếm số phần trăm của giá ban đầu là:
100% − 25% = 75%.
Giá mới của quyển sách sau khi giảm giá 25% là:
48 000 . 75% = 36 000 (đồng).
Vậy giá mới của quyển sách sau khi giảm giá 25% là 36 000 đồng.
Cách 2: Tính số tiền được giảm khi mua quyển sách sau đó tính giá mới của quyển sách sau khi giảm.
Quyển sách giảm đi số tiền là:
48 000 . 25% = 48 000 .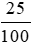 
= 12 000 ( đồng).
Giá mới của quyển sách là:
48 000 − 12 000 = 36 000 ( đồng).
Vậy giá mới của quyển sách sau khi giảm giá 25% là 36 000 đồng.
b) Cách 1: Tính số phần trăm giá mới của quyển sách so với giá ban đầu sau đó tính giá mới.
Giá ban đầu của quyển sách chiếm 100% và tăng giá 10% so với giá ban đầu.
Giá của quyển sách khi tăng chiếm số phần trăm của giá ban đầu là:
100% + 10% = 110%.
Giá mới của quyển sách sau khi tăng giá 10% là:
48 000 . 110% = 48 000 .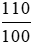 
= 52 800 (đồng).
Vậy giá mới của quyển sách sau khi tăng giá 10% là 52 800 đồng.
Cách 2: Tính số tiền tăng thêm khi mua quyển sách sau đó tính giá mới của quyển sách sau khi tăng.
Quyển sách tăng thêm số tiền là:
48 000 . 10% = 48 000 .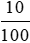 
= 4 800 ( đồng).
Giá mới của quyển sách là:
48 000 + 4 800 = 52 800 ( đồng).
Vậy giá mới của quyển sách sau khi tăng giá 10% là 52 800 đồng.
Lời giải:
Lượng cafein có trong 300g cà phê Arabica là:
300 . 1,5% = 300 .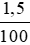 
= 4,5 (g).
Vậy lượng cafein có trong 300 g cà phê Arabica là 4,5 g.
Lời giải:
Khối lượng bột ngọt có trong 20 g bột nêm là:
20 . 60% = 20 .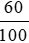 
= 12 (gam).
Vậy khối lượng bột ngọt có trong 20 g bột nêm là 12 gam.
Lời giải:
1 năm = 12 tháng.
Cách tính tiền lãi có kì hạn là:
Số tiền lãi = Số tiền gửi . lãi suất (%/năm) . số tháng gửi : 12.
Sau một năm bác Tám nhận được số tiền lãi là:
50 . 8% .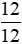 
= 50 . 
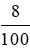= 4 (triệu đồng) = 4 000 000 (đồng).
Vậy sau một năm bác Tám nhận được số tiền lãi là 4 000 000 đồng.
Lời giải:
Cách tính tiền lãi không có kì hạn là:
Tính số tiền lãi = Số tiền gửi . lãi suất (% / năm) . số ngày thực gửi : 360.
Số tiền lãi mẹ Lan nhận được sau 90 ngày là:
800 . 0,6% .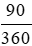 
= 800 . 
. 
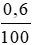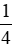= 1,2 (triệu đồng)
Sau 90 ngày, khi rút ra mẹ Lan nhận được số tiền cả vốn lẫn lãi là:
800 + 1,2 = 801,2 (triệu đồng) = 801 200 000 (đồng).
Vậy sau 90 ngày, khi rút ra mẹ Lan nhận được số tiền 801 200 000 đồng cả vốn lẫn lãi.
Lời giải:
Số ki-lô-gam đậu nành để có thể thu được 6,4 kg chất đạm là:
6,4 : 32% = 6,4 :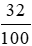 
= 6,4 . 
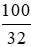= 20 ( kg)
Vậy phải nấu chín 20 ki-lô-gam đậu nành loại đó để có thể thu được 6,4 kg chất đạm.
Lời giải:
Bản đồ có tỉ lệ 1: 50 000 nghĩa là chiều dài thật của cây cầu gấp 50 000 lần chiều dài trên bản đồ.
Chiều dài thật của cầu Cần Thơ là:
5,5 . 50 000 = 275 000 (cm) = 2,75 (km).
Vậy chiều dài thật của cầu Cần Thơ là 2,75 km.
Lời giải:
Bản đồ có tỉ lệ 1 : 50 nghĩa là chiều dài thật của chiếc xe ô tô gấp 50 lần chiều dài trên bản đồ.
Chiều dài thật của chiếc xe ô tô đó là:
9,4 . 50 = 470 (cm) = 4,7 (m).
Vậy chiều dài thật của chiếc xe ô tô đó là 4,7 m.
Xem thêm các bài giải SGK Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Tỉ số và tỉ số phần trăm
Lý thuyết Bài toán về tỉ số phần trăm
1. Tìm giá trị phần trăm của một số
Muốn tìm giá trị a% của số b, ta tính: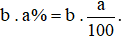 
.
Ví dụ 1. 22,5% của 34 là: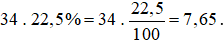 
.
2. Tìm một số khi biết giá trị phần trăm của số đó
Muốn tìm số b khi biết a% của b là c, ta tính: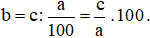 
.
Ví dụ 2. Số có giá trị 12,5% bằng 250 là:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
