Với giải bài tập Toán lớp 6 Bài tập cuối chương 6 chi tiết bám sát nội dung sgk Toán 6 Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài tập cuối chương 6
Video giải Toán 6 Chương 6: Số thập phân – Chân trời sáng tạo
A. Các câu hỏi phần trắc nghiệm
Giải Toán 6 trang 50 Tập 2 Chân trời sáng tạo
Câu 1 trang 50 Toán lớp 6 Tập 2: Trong các phát biểu sau, phát biểu nào đúng?
(A)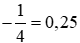 
.
(B)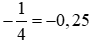
.
(C)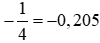
.
(D)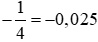
.
Lời giải:
Ta đưa phân số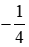 
về dạng số thập phân rồi chọn phát biểu đúng, ta thực hiện:
Cách 1: Đưa phân số ban đầu về phân số thập phân sau đó chuyển về số thập phân.
- Đưa phân số ban đầu về phân số thập phân: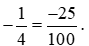 
- Chuyển từ phân số thập phân về số thập phân (bằng cách thực hiện phép chia tử số cho 100), ta được:
.
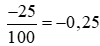Do đó,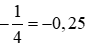 
Vậy phát biểu đúng là (B) .
Cách 2: Phân số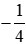 
là phép chia (−1) cho 4. Thực hiện phép chia (−1) cho 4, ta được:
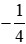= (−1) : 4 = −(1 : 4) = −0,25.
Do đó,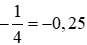 
.
Vậy phát biểu đúng là: (B)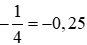 
.
Câu 2 trang 50 Toán lớp 6 Tập 2: Trong các phát biểu sau, phát biểu nào sai?
(A) 0, 3 > −0, 4.
(B) −0,9 > −0,99.
(C) −2,125 < 0.
(D) −0,555 < −0,666.
Lời giải:
(A) 0, 3 > −0, 4.
Nhận thấy: 0,3 là số thập phân dương; −0, 4 là số thập phân âm.
Mà số thập phân dương luôn lớn hơn số thập phân âm.
Do đó phát biểu (A) đúng.
(B) −0,9 > −0,99.
- Số đối của các số −0,9; −0,99 lần lượt là 0,9; 0,99.
- Phần nguyên của hai số 0,9; 0,99 đều là 0.
- Phần thập phân:
+ Chữ số hàng phần mười của hai số 0,9; 0,99 đều là 9.
+ Chữ số hàng phần trăm của số 0,9 và 0,99 lần lượt là 0 và 9. Vì 0 < 9 nên 0,9 < 0,99 hay −0,9 > −0,99.
Do đó phát biểu (B) đúng.
(C) −2,125 < 0.
Nhận thấy: số −2,125 là số thập phân âm.
Mà số thập phân luôn bé hơn số 0.
Do đó phát biểu (C) đúng.
(D) −0,555 < −0,666.
- Số đối của các số −0,555; −0,666 lần lượt là 0,555; 0,666.
- Phần nguyên của hai số 0,555; 0,666 đều là 0.
- Phần thập phân: Chữ số hàng phần mười của số 0,555; 0,666 lần lượt là 5 và 6. Vì 5 < 6 nên 0,555 < 0,666 hay −0,555 > −0,666.
Do đó phát biểu (D) sai.
Vậy phát biểu sai là: (D) −0,555 < −0,666.
Câu 3 trang 50 Toán lớp 6 Tập 2: Kết quả của phép tính là:
8 . (−0,125) . (−0,25) . (−400).
(A) 100.
(B) 200.
(C) −100.
(D) −20.
Lời giải:
Ta có: 8 . (−0,125) . (−0,25) . (−400)
= [8 . (−0,125)] . [(−0,25) . (−400)] (tính chất kết hợp)
= [−(8 . 0,125)] . [0,25 . 400]
= (−1) . 100 = −100.
Do đó: 8 . (−0,125) . (−0,25) . (−400) = −100.
Vậy kết quả của phép tính là: (C) −100.
Câu 4 trang 50 Toán lớp 6 Tập 2: Giá trị 25% của 80 là:
(A) 250.
(B) 25.
(C) 200.
(D) 20.
Lời giải:
Giá trị 25% của 80 là:
80 . 25% = 80 .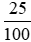
= 20.
Vậy giá trị 25% của 80 là: (D) 20.
B. Bài tập phần tự luận
Bài 1 trang 50 Toán lớp 6 Tập 2: Hãy sắp xếp các số thập phân sau theo thứ tự giảm dần:
−3,43; −3,4; 0,2; 3,43; 3,4; 0,22.
Lời giải:
Để sắp xếp các số thập phân sau theo thứ tự giảm dần, ta làm như sau:
Bước 1: Chia thành 2 nhóm số thập phân dương và số thập phân âm, vì số thập phân dương luôn lớn hơn số thập phân âm.
Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:
- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.
- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.
Đối với bài toán này, ta thực hiện theo thứ tự các bước như trên:
* Phân loại:
- Nhóm các số thập phân dương: 0,2; 3,43; 3,4; 0,22.
- Nhóm các số thập phân âm: −3,43; −3,4.
* So sánh các số thập phân trong theo nhóm:
- Nhóm các số thập phân dương:
+ Hai số 0,2 và 0,22 đều có phần nguyên là 0; ta so sánh phần thập phân:
• Hàng phần mười của hai số 0,2 và 0,22 đều là 2.
• Hàng phần trăm của hai số 0,2 và 0,22 lần lượt là 0 và 2.
Vì 2 > 0 nên 0,22 > 0,2.
+ Hai số 3,43 và 3,4 đều có phần nguyên là 3; ta so sánh phần thập phân:
• Hàng phần mười của hai số 3,43 và 3,4 đều là 4.
• Hàng phần trăm của hai số 3,43 và 3,4 lần lượt là 3 và 0.
Vì 3 > 0 nên 3,43 > 3,4.
Do đó 3,43 > 3,4 > 0,22 > 0,2.
- Nhóm các số thập phân âm:
+ Số đối của các số −3,43; −3,4 lần lượt là 3,43; 3,4.
Ở trên ta đã chứng minh được: 3,43 > 3,4 nên −3,43 < −3,4.
Từ đó, ta suy ra: 3,43 > 3,4 > 0,22 > 0,2 > −3,4 > −3,43.
Vậy các số được sắp xếp thứ tự giảm dần là: 3,43; 3,4; 0,22; 0,2; −3,4; −3,43.
Bài 2 trang 50 Toán lớp 6 Tập 2: Hãy sắp xếp các số thập phân sau theo thứ tự tăng dần:
1,23; −1,23; 0,12; 0,121; −0,02; −0,002; 0,1.
Lời giải:
Để sắp xếp các số thập phân sau theo thứ tự tăng dần, ta làm như sau:
Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.
Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:
- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.
- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.
Đối với bài toán này, ta thực hiện theo thứ tự các bước như trên:
* Phân loại:
- Nhóm các số thập phân dương: 1,23; 0,12; 0,121; 0,1.
- Nhóm các số thập phân âm: −1,23; −0,002; −0,02.
* So sánh các số thập phân trong theo nhóm:
- Nhóm các số thập phân dương:
+ Số 1,23 có phần nguyên là 1.
+ Các số 0,12; 0,121; 0,1 có cùng phần nguyên là 0 nên ta so sánh phần thập phân:
• Hàng phần mười của các số 0,12; 0,121; 0,1 đều là 1.
•) Hàng phần trăm của số 0,1 đều là 0.
•) Hàng phần trăm của hai số 0,12 và 0,121 đều là 2. Hàng phần nghìn của hai số 0,12 và 0,121 lần lượt là 0 và 1. Vì 0 < 1 nên 0,12 < 0,121.
Do đó, 0,1 < 0,12 < 0,121 < 1,23.
- Nhóm các số thập phân âm:
+ Số đối của các số −1,23; −0,02; −0,002 lần lượt là 1,23; 0,02; 0,002.
+ Số 1,23 có phần nguyên là 1;
+ Số 0,02 và 0,002 đều có phần nguyên là 0; ta so sánh phần thập phân:
• Hàng phần mười của hai số 0,02 và 0,002 đều là 0.
•) Hàng phần trăm của hai số 0,02 và 0,002 lần lượt là 2 và 0.
Vì 2 > 0 nên 0,02 > 0,002 hay −0,02 < −0,002.
Do đó −1,23 < −0,02 < −0,002.
Từ đó ta suy ra −1,23 < −0,02 < −0,002 < 0,1 < 0,12 < 0,121 < 1,23.
Vậy các số được sắp xếp thứ tự tăng dần là: −1,23; −0,02; −0,002; 0,1; 0,12; 0,121; 1,23.
Lời giải:
Nhiệt độ sôi của oxi cao hơn nhiệt độ sôi của nito là:
–182,95 – (–195,79) = –182,95 + 195,79 = 195,79 –182,95 = 12,84 (°C).
Vậy nhiệt độ sôi của oxi cao hơn nhiệt độ sôi của nito là 12,84 °C.
Lời giải:
Tổng số nhân viên trong công ty là:
30 + 24 = 54 ( người)
Số nhân viên nữ chiếm số phần trăm trong tổng số nhân viên công ty là:
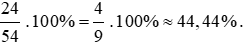
Vậy số nhân viên nữ chiếm 44,44% trong tổng số nhân viên công ty.
Lời giải:
Tổng số hàng đã may được là:
25 + 35 = 60 (chiếc)
Số lượng áo chiếm số phần trăm trong tổng số hàng may được là:
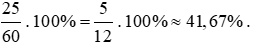
Vậy số lượng áo chiếm số phần trăm trong tổng số hàng may được là 41,67 %.
a) Vậy công ty đã hoàn thành bao nhiêu phần trăm so với mục tiêu ban đầu?
b) Công ty đã hoàn thành vượt mức đề ra là bao nhiêu phần trăm?
Lời giải:
a) Công ty đã hoàn thành số phần trăm so với mục tiêu ban đầu là:
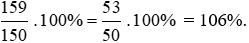
Vậy công ty đã hoàn thành 106% so với mục tiêu ban đầu.
b) Công ty đã hoàn thành vượt mức đề ra số phần trăm là:
106% – 100% = 6%.
Vậy công ty đã hoàn thành vượt mức đề ra là 6%.
Lời giải:
Tổng tiền hàng chiếm 100% và tiền thuế VAT chiếm 10% so với tổng tiền hàng.
Tổng tiền hàng và tiền thuế chiếm số phần trăm là:
100% + 10% = 110%.
Nếu không tính thuế VAT thì người đó phải trả số tiền cho món hàng là:
2 915 000 : 110% = 2 915 000 :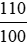 
= 2 915 000 . 
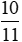= 2 623 500 (đồng).
Vậy nếu không tính thuế VAT thì người đó phải trả số tiền cho món hàng là 2 623 500 đồng.
Xem thêm các bài giải SGK Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 5: Bài toán về tỉ số phần trăm
Bài 3: Vai trò của tính đối xứng trong thế giới tự nhiên
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
