Với giải bài tập Toán lớp 6 Bài 4: Tỉ số và tỉ số phần trăm chi tiết bám sát nội dung sgk Toán 6 Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài 4: Tỉ số và tỉ số phần trăm
Video giải Toán 6 Bài 4: Tỉ số và tỉ số phần trăm – Chân trời sáng tạo
A. Các câu hỏi trong bài
Giải Toán 6 trang 41 Tập 2 Chân trời sáng tạo
b) Trí và Dũng mỗi em câu được một con cá lóc. Con cá của Trí cân nặng 900g, con cá của Dũng nặng 1,3 kg. Hỏi con cá của Dũng nặng gấp bao nhiêu lần con cá của Trí?
c) Đoạn thẳng AB dài 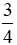 m và đoạn thẳng CD dài 50 cm. Hỏi đoạn AB dài gấp bao nhiêu lần đoạn CD?
m và đoạn thẳng CD dài 50 cm. Hỏi đoạn AB dài gấp bao nhiêu lần đoạn CD?
Lời giải:
Để tính một số a bằng bao nhiêu lần số b, ta lấy a : b.
a) Thời gian Mai làm lâu gấp số lần thời gian Lan làm là:
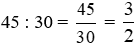 (lần).
(lần).
Vậy thời gian Mai làm lâu gấp 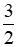 lần thời gian Lan làm.
lần thời gian Lan làm.
b) Đổi 1,3 kg = 1300 g.
Con cá của Dũng nặng gấp số lần con cá của Trí là:
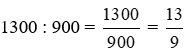 (lần).
(lần).
Vậy con cá của Dũng nặng gấp 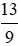 lần con cá của Trí.
lần con cá của Trí.
c) Đổi  m =
m = 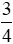 .100 cm = 75 cm.
.100 cm = 75 cm.
Đoạn AB dài gấp số lần đoạn CD là:
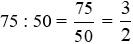 (lần).
(lần).
Vậy đoạn AB dài gấp 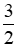 lần đoạn CD.
lần đoạn CD.
Giải Toán 6 trang 42 Tập 2 Chân trời sáng tạo
a) 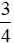 m và 25 cm;
m và 25 cm;
b) 30 phút và 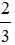 giờ;
giờ;
c) 0,4 kg và 340 g;
d) 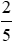 m và
m và 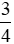 m.
m.
Lời giải:
Tỉ số của hai đại lượng a và b là a : b = (b ≠ 0; a, b cùng đơn vị đo).
a) Đổi 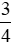 m =
m = 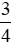 . 100 cm = 75 cm.
. 100 cm = 75 cm.
Tỉ số của hai đại lượng 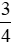 m và 25 cm hay tỉ số của 75 cm và 25 cm là:
m và 25 cm hay tỉ số của 75 cm và 25 cm là:
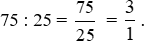
Vậy tỉ số của hai đại lượng 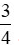 m và 25 cm là 3.
m và 25 cm là 3.
b)  giờ =
giờ =  . 60 phút = 40 phút;
. 60 phút = 40 phút;
Tỉ số của hai đại lượng 30 phút và  giờ hay tỉ số của 30 phút và 40 phút là:
giờ hay tỉ số của 30 phút và 40 phút là:
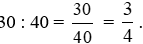
Vậy tỉ số của hai đại lượng 30 phút và  giờ là
giờ là 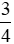 .
.
c) Đổi 0,4 kg = 400 g;
Tỉ số của hai đại lượng 0,4 kg và 340 g hay tỉ số của 400 g và 340 g là:
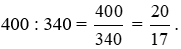
Vậy tỉ số của hai đại lượng 0,4 kg và 340 g là 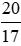 .
.
d) Tỉ số của hai đại lượng  m và
m và 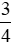 m là:
m là:
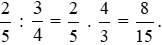
Vậy tỉ số của hai đại lượng  m và
m và 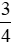 m là
m là 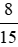 .
.

Lời giải:
Hai bát rưỡi nước tức là  bát nước.
bát nước.
Tỉ số giữa thể tích nước và gạo là:
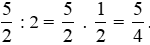
Vậy tỉ số giữa thể tích nước và gạo trong cách nấu cơm này là 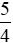 .
.
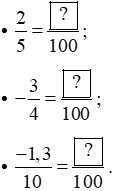
b) Cơ thể người có khoảng 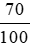 là nước. Hùng cân nặng 40 kg, em hãy cho biết khối lượng nước có trong cơ thể Hùng.
là nước. Hùng cân nặng 40 kg, em hãy cho biết khối lượng nước có trong cơ thể Hùng.
Lời giải:
a)
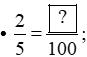
- Chia cả mẫu số của phân số thứ hai cho phân số thứ nhất: 100 : 5 = 20.
- Nhân cả tử số và mẫu số của phân số thứ nhất với 20, ta được:
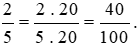
Vậy 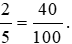
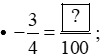
- Chia cả mẫu số của phân số thứ hai cho phân số thứ nhất: 100 : 4 = 25.
- Nhân cả tử số và mẫu số của phân số thứ nhất với 25, ta được:
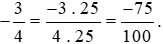
Vậy 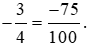
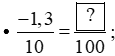
- Chia cả mẫu số của phân số thứ hai cho phân số thứ nhất: 100 : 10 = 10.
- Nhân cả tử số và mẫu số của phân số thứ nhất với 10, ta được:
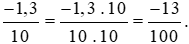
Vậy 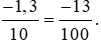
b) Khối lượng nước trong cơ thể Hùng là:
40 . 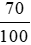 = 28 (kg).
= 28 (kg).
Vậy khối lượng nước trong cơ thể Hùng là 28 kg.
Giải Toán 6 trang 43 Tập 2 Chân trời sáng tạo
Thực hành 2 trang 43 Toán lớp 6 Tập 2: Tính tỉ số phần trăm của hai số cho trong mỗi trường hợp sau:
a) 3 và 4;
b) −2,66 và 200;
c) 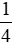 và 0,5.
và 0,5.
Lời giải:
a) Tỉ số phần trăm của hai số 3 và 4 là:
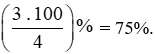
Vậy tỉ số phần trăm của hai số 3 và 4 là 75%.
b) Tỉ số phần trăm của hai số −2,66 và 200 là:
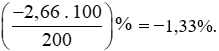
Vậy tỉ số phần trăm của hai số −2,66 và 200 là −1,33%.
c) Tỉ số phần trăm của hai số 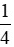 và 0,5 là:
và 0,5 là:
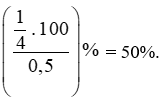
Vậy tỉ số phần trăm của hai số 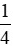 và 0,5 là 50%.
và 0,5 là 50%.
Lời giải:
Tỉ số phần trăm của doanh thu tháng Năm so với tháng Tư là:
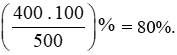
Vậy tỉ số phần trăm của doanh thu tháng Năm so với tháng Tư là 80%.
B. Bài tập
Giải Toán 6 trang 44 Tập 2 Chân trời sáng tạo

Lời giải:
Tỉ số giữa số học sinh học bơi và sĩ số lớp là:
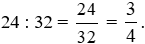
Vậy tỉ số giữa số học sinh học bơi và sĩ số lớp là 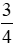 .
.
Bài 2 trang 44 Toán lớp 6 Tập 2: Viết các số thập phân sau đây dưới dạng tỉ số phần trăm:
−0,72; 0,4; −2,23.
Lời giải:
Các số thập phân được viết dưới dạng tỉ số phần trăm như sau:
−0,72 = −0,72 . 100% =−72%;
0,4 = 0,4 . 100% = 40%;
−2,23 = −2,23 . 100% = −223%.
Bài 3 trang 44 Toán lớp 6 Tập 2: Viết các phân số sau dưới dạng tỉ số phần trăm:
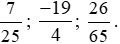
Lời giải:
Để viết các phân số dưới dạng tỉ số phần trăm, ta làm như sau:
Bước 1: Viết các phân số dưới dạng phân số có mẫu là 100.
Bước 2: Thêm kí hiệu % vào sau tử số của phân số mới.
Các phân số được viết dưới dạng tỉ số phần trăm là:
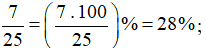
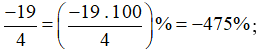
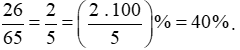
Bài 4 trang 44 Toán lớp 6 Tập 2: Viết các tỉ số phần trăm sau dưới dạng số thập phân:
−5%; −35%; 317%.
Lời giải:
Để viết các tỉ số phần trăm dưới dạng số thập phân, ta làm như sau:
Bước 1: Viết các tỉ số phần trăm dưới dạng phân số có mẫu là 100.
Bước 2: Sau đó chuyển phân số có mẫu là 100 về số thập phân.
Các tỉ số phần trăm viết dưới dạng số thập phân là:
−5% = 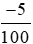 = - 0,05;
= - 0,05;
−35% = 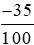 = - 0,35;
= - 0,35;
317% = 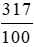 = 3,17.
= 3,17.
Lời giải:
Tỉ số phần trăm học sinh giỏi của lớp là:
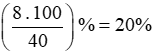
Tỉ số phần trăm học sinh khá của lớp là:
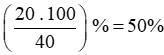
Tỉ số phần trăm học sinh trung bình của lớp là:
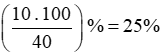
Tỉ số phần trăm học sinh yếu kém của lớp là:
100% − 20% − 50% − 25% = 5%.
Vậy tỉ số phần trăm học sinh giỏi, khá, trung bình, yếu kém của lớp lần lượt là 20%, 50%, 25%, 5%.
Lời giải:
Tỉ số phần trăm giữa số trang in và số trang viết tay là:
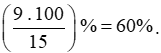
Vậy tỉ số phần trăm giữa số trang in và số trang viết tay là 60%.
Lời giải:
Phần trăm tăng trưởng của tháng Hai so với tháng Một là:
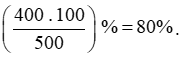
Vậy phần trăm tăng trưởng của tháng Hai so với tháng Một là 80%.
Lời giải:
Đổi 56 km = 5 600 000 cm.
Tỉ lệ của bản đồ là:
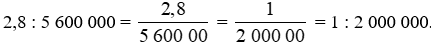
Vậy tỉ lệ của bản đồ là 1 : 2 000 000.
Xem thêm các bài giải SGK Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Làm tròn số thập phân và ước lượng kết quả
Bài 5: Bài toán về tỉ số phần trăm
Lý thuyết Tỉ số và tỉ số phần trăm
1. Tỉ số của hai đại lượng
Ta gọi thương trong phép chia số a cho số b (b ≠0) là tỉ số của a và b.
Tỉ số của a và b kí hiệu là a : b (cũng kí hiệu là 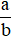 ).
).
Ví dụ 1.
- Tỉ số của hai số 16 và 37 được kí hiệu là 16 : 37 hay 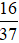 .
.
- Tỉ số của hai số 3,6 và 8,25 được kí hiệu là 3,6 : 8,25 hay 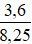 .
.
Chú ý:
- Phân số 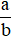 thì cả a và b phải là các số nguyên.
thì cả a và b phải là các số nguyên.
- Tỉ số 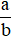 thì a và b có thể là các số nguyên, phân số, hỗn số, số thập phân,…
thì a và b có thể là các số nguyên, phân số, hỗn số, số thập phân,…
- Ta thường dùng khái niệm tỉ số nói về thương của hai đại lượng cùng loại và cùng đơn vị đo.
Ví dụ 2. Tính tỉ số của hai đại lượng được cho trong các trường hợp sau:
a) 0,6 kg và 260 g;
b) 15 phút và  giờ.
giờ.
Lời giải:
a) Đổi 0,6 kg = 600 g
Tỉ số của hai đại lượng 0,4 kg và 340 g hay tỉ số của 400 g và 340 g là:
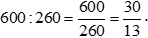 .
.
Vậy tỉ số của hai đại lượng 0,6 kg và 260 g là 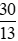 .
.
b) 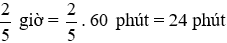
Tỉ số của hai đại lượng 15 phút và  giờ hay tỉ số của 15 phút và 24 phút là:
giờ hay tỉ số của 15 phút và 24 phút là:
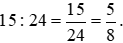
Vậy tỉ số của hai đại lượng 15 phút và  giờ là
giờ là  .
.
2. Tỉ số phần trăm của hai đại lượng
Trong thực hành, ta thường dùng tỉ số dưới dạng tỉ số phần trăm với kí hiệu % thay cho 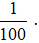 .
.
Để tính tỉ số phần trăm của hai số a và b, ta nhân a với 100 rồi chia cho b và viết kí hiệu % vào bên phải kết quả tìm được.
Ví dụ 3. Tính tỉ số phần trăm của hai số cho trong mỗi trường hợp sau:
a) 2 và 8;
b)  và 3,125.
và 3,125.
Lời giải:
a) Tỉ số phần trăm của hai số 2 và 8 là:
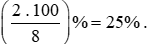
Vậy tỉ số phần trăm của hai số 2 và 8 là 25%.
b) Tỉ số phần trăm của hai số  và 3,125 là:
và 3,125 là:
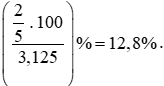
Vậy tỉ số phần trăm của hai số  và 3,125 là 12,8%.
và 3,125 là 12,8%.