Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 1: Góc ở tâm. Số đo cung chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 1: Góc ở tâm. Số đo cung
Từ giờ đến giờ kim giờ quay được góc ở tâm bằng bao nhiêu độ
Cũng hỏi như thế từ giờ đến giờ
Phương pháp giải:
Ta sử dụng kiến thức: Góc ở có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
Lời giải:
Vì trên đồng hồ có 12 chữ số nên mặt đồng hồ được chia ra thành cung tròn bằng nhau, mỗi cung tròn tương ứng với góc ở tâm bằng
Từ giờ đến giờ thì kim giờ quay được một góc ở tâm bằng
Từ giờ đến giờ thì kim giờ quay được một góc ở tâm bằng
Lời giải:
Một vòng quay của kim phút là 60 phút tương ứng với 360°. Như vậy mỗi phút tương ứng với Đồng hồ chạy chậm 25 phút thì phải quay kim phút một góc ở tâm là
Muốn cắt chỉ bằng một nhát kéo thì phải gấp tờ giấy đó thành một hình có góc ở tâm bằng bao nhiều độ
Phương pháp giải:
Ta sử dụng kiến thức: Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
Lời giải:
Đầu tiên ta gấp đôi tờ giấy, ta chọn điểm làm tâm rồi chia tờ giấy ra thành phần với góc ở tâm bằng nhau, mỗi góc bằng
Tính số đo góc ở tâm
Phương pháp giải:
Ta sử dụng kiến thức:
+) Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
+) Nếu một đường thẳng là tiếp điểm của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
Lời giải:
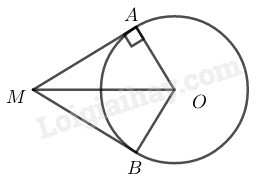
Xét đường trong có: (tính chất tiếp tuyến)
Trong có ta có:
Lại có là tia phân giác của góc (tính chất tiếp tuyến MA, MB cắt nhau nhau tại M)
Suy ra
Phương pháp giải:
Ta sử dụng kiến thức:
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+) Trong tam giác đều mỗi góc bằng .
+) Số đo của nửa đường tròn bằng
Lời giải:
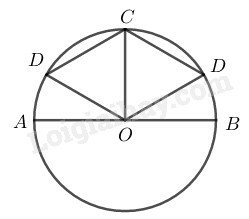
Điểm có 2 trường hợp :
Nếu điểm nằm giữa và
Ta có điểm chính giữa của cung nên:
Ta lại có
Suy ra :
đều
Suy ra
Nếu nằm giữa và ta có :
đều
Suy ra
Số đo cung nhỏ của lớn hơn số đo cung nhỏ của
Số đo cung lớn của nhỏ hơn số đo cung lớn của
Số đo hai cung nhỏ bằng nhau.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Số đo của cung lớn bằng hiệu giữa và số đo cung nhỏ(có chung hia mút với cung lớn).
+) Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.
+) Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.
+) Hai cung được là bằng nhau nếu chúng có số đo bằng nhau.
+) Số đo của cung nhỏ bằng số đo góc ở tâm chắn cung đó.
Lời giải:
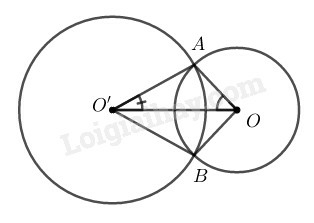
Trong ta có: (nhỏ)
Trong ta có: (nhỏ)
Vì số đo cung nhỏ của lớn hơn số đo cung nhỏ của
Suy ra:
Xét hai tam giác và có:
+)
+)
+) cạnh chung
Nên
Từ và suy ra:
Trong ta có:
Suy ra: (bất đẳng thức tam giác) hay
Chú ý: Nếu các em vẽ hình như dưới đây thì ta lấy đối xứng đường tròn qua trục để chứng minh như trên.
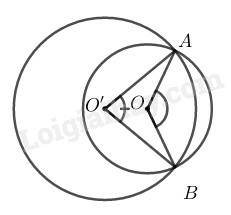
Trong số đo cung lớn cộng với số đo cung nhỏ bằng
Mà số đo cung lớn của nhỏ hơn số đo cung lớn của
Suy ra số đo cung nhỏ của lớn hơn số đo cung nhỏ của
Chứng minh tương tự câu ta có:
Số đo hai cung nhỏ của và bằng nhau
Suy ra: cân tại nên hay
Hãy so sánh các góc ở tâm và
Hướng dẫn. Sử dụng các tam giác cân
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong tam giác cân, hai góc ở đáy bằng nhau.
+) Góc có đỉnh trùng với tâm đường tròn gọi là góc ở tâm.
Lời giải:
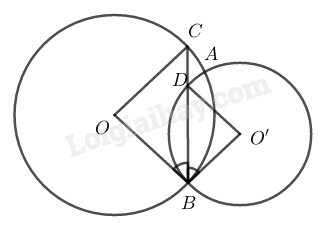
Trong ta có:
cân tại (vì bán kính)
Trong ta có:
cân tại (vì bán kính)
Lại có (vì là phân giác của )
Từ và suy ra: .
Ta sử dụng kiến thức:
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+) Số đo của cung lớn bằng hiệu giữa và số đo cung nhỏ (có chung hai đầu mút với cung lớn).
Lời giải:
Vì cung nhận làm điểm chính giữa, cung nhận là điểm chính giữa nên
Kẻ đường kính ta có:
(hai góc kề bù)
Suy ra: (hai góc đối đỉnh)
(hai góc kề bù)
Hướng dẫn: Xét trường hợp:
Tia nằm trong góc đối đỉnh của góc ở tâm
Tia trùng với tia đối của một cạnh của góc ở tâm
Tia nằm trong một góc kề bù với góc ở tâm
Phương pháp giải:
Ta sử dụng kiến thức:
+) Nếu là một điểm trên cung thì:
+) Số đo của nửa đường tròn bằng
+) Số đo của cung lớn bằng hiệu giữa và số đo cung nhỏ (có chung hai đầu mút với cung lớn).
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Lời giải:
Trường hợp tia nằm trong góc đối đỉnh với
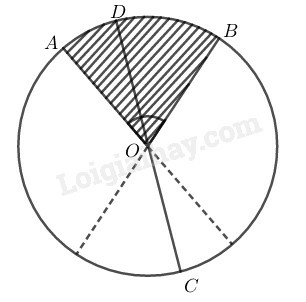
Kẻ đường kính
Suy ra: nằm giữa và nên điểm nằm trên cung nhỏ cung
Vì nằm giữa và nên điểm nằm trên cung nửa đường tròn
Vì nằm giữa và nên điểm nằm trên cung nửa đường tròn
Cộng từng vế và
Từ và suy ra:
Mà
Vậy với cung lớn ta có:
b) Trường hợp tia trùng với tia đối của một cạnh của góc ở tâm
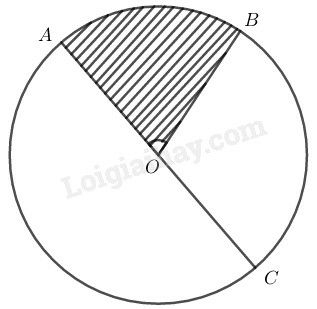
Do tia trùng với tia đối của một cạnh của góc ở tâm , ta có:
;
Suy ra:
Vậy với cung lớn ta có:
c) Trong hợp tia nằm trong góc kề bù với góc ở tâm
Kẻ đường kính
Theo trường hợp ta có:
Ta xét trường hợp nằm trên cung nhỏ
Theo kết quả trường hợp ta có:
Vậy với cung lớn ta có:
Trong trường hợp nằm trên góc đối với góc ở tâm chứng minh tương tự.
Trong trường hợp nằm trên góc đối đỉnh với góc ở tâm chứng minh ở trường hợp
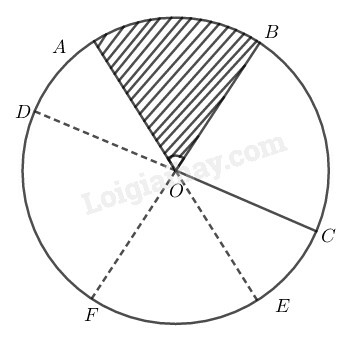
Bài tập bổ sung (trang 100 SBT Toán 9)
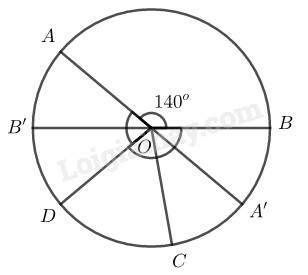
Đọc tên các góc ở tâm có số đo nhỏ hơn
Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên.
Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn ).
So sánh hai cung nhỏ và
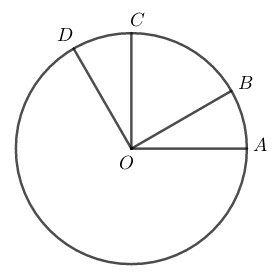
Phương pháp giải:
Ta sử dụng kiến thức:
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+) Cung nhỏ có số đo nhỏ hơn
+) Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.
Lời giải:
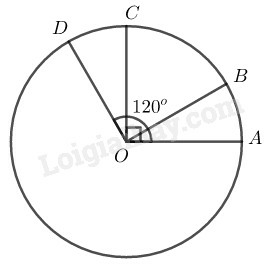
Các góc ở tâm có số đo nhỏ hơn là:
Các cung có số đo bằng nhau nhỏ hơn là:
Suy ra: gấp đôi
Đọc tên các góc ở tâm có số đo không lớn hơn
Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên.
Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn ).
So sánh hai cung nhỏ và
Phương pháp giải:
Ta sử dụng kiến thức:
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+) Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.
+) Cung nhỏ có số đo nhỏ hơn
Lời giải:
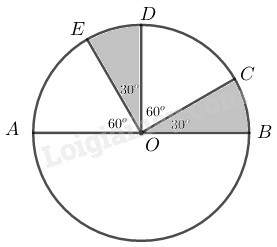
Các góc ở tâm có số đo không quá là:
Ta có:
Ta có:
Ta có: sđ
Ta có:
Các cung có số đo nhỏ hơn bằng nhau.
; ; ; ; .
Ta có số đo của cung gấp đôi số đo của cung .