Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu "Chuyên đề tích phân luyện thi THPT quốc gia" Toán lớp 12, tài liệu bao gồm 78 trang, đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

 A. Lý thuyết Tích phân

1. Khái niệm và tính chất

a. Định nghĩa

Cho hàm số $f(x)$ liên tục trên đoạn $[a;b]$. Giả sử $F(x)$ là một nguyên hàm của hàm số $f(x)$ trên đoạn $[a;b]$, hiệu số $F(b)-F(a)$ được gọi là tích phân từ $a$ đến $b$ (hay tích phân xác định trên đoạn $[a;b]$ của hàm số $f(x)$.

Kí hiệu là : ${\int }_a^{b}f(x)dx$

Vậy ta có :${\int }_a^{b}f(x)dx=F(b)-F(a)=F(x){|}_a^b$

Chú ý : Trong trường hợp a = b, ta định nghĩa: ${\int }_a^{a}f(x)dx=0$

Trường hợp a>b, ta định nghĩa: ${\int }_a^{b}f(x)dx=-{\int }_b^{a}f(x)dx$

Tích phân không phụ thuộc vào chữ dùng làm biến số trong dấu tích phân, tức là :

${\int }_a^{b}f(x)dx={\int }_a^{b}f(t)dt={\int }_a^{b}f(u)du=...$ (vì đều bằng $F(b)-F(a)$)

b. Tính chất của tích phân

${\int }_a^{b}kf(x)dx=k{\int }_a^{b}f(x)dx$  ( với $k$ là hằng số)

${\int }_a^b\left[f\left(x\right)\pm g\left(x\right)\right]d\mathrm{x}={\int }_a^{b}f\left(x\right)d\mathrm{x}\pm {\int }_a^{b}g\left(x\right)d\mathrm{x}$

${\int }_a^{b}f(x)dx={\int }_a^{c}f(x))dx+{\int }_c^{b}f(x)dx$ (với $a<b<c$)

2. Phương pháp tinh tích phân

a. Phương pháp đổi biến số

Định lí. Cho hàm số $f(x)$ liên tục trên $[a;b]$. Giả sử hàm số $x=\phi \left(t\right)$ có đạo hàm liên tục trên đoạn $[\alpha ;\beta ]$ sao cho $\phi \left(\alpha \right)=a,\phi \left(\beta \right)=b$ và $a\le \phi \left(t\right)\le b,\mathrm{\forall }t\in \left[\alpha ;\beta \right]$. Khi đó:

${\int }_a^{b}f(x)dx={\int }_{\alpha }^{\beta }f(\phi \left(t\right)){\phi }^{\prime }(t)dt$

Chú ý. Có thể dử dụng phép biến đổi số ở dạng sau:

Cho hàm số f(x) liên tục trên đoạn [a;b]. Giả sử hàm số u=u(x) có đạo hàm liên tục trên đoạn [a;b] sao cho α ≤ u(x) ≤ β, ∀ x∈ [a;b]. Nếu f(x) =g[u(x)].u^’(x) ∀ x∈ [a;b], trong đó g(u) liên tục trên đoạn [α;β] thì: 

${\int }_a^{b}f(x)dx={\int }_{u(a)}^{u(b)}g(u)du$

b. Phương pháp tính tích phân từng phần

Định lí. Nếu u =u(x) và v=v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a;b], thì :

${\int }_a^{b}u(x)v^{\prime }(x)dx=[u(x)v(x)]{|}_a^b-{\int }_a^b{u}^{\prime }(x)v(x)dx$

hay ${\int }_a^{b}udv=uv{|}_a^b-{\int }_a^{b}vdu$

3. Bất đẳng thức (phần kiến thức bổ sung)

Nếu f(x) liên tục và không âm trên đoạn [a;b] thì : ${\int }_a^{b}f(x)dx\ge 0$

Từ đó ta có:

Nếu g(x), f(x) liên tục trên đoạn [a;b] và 0 ≤ g(x) ≤ f(x), ∀ x ∈ [a;b] thì

${\int }_a^{b}g(x)dx\le {\int }_a^{b}f(x)dx$

Dấu " = " xảy ra khi và chỉ khi g(x) ≡ f(x).

Suy ra: Nếu f(x) liên tục trên đoạn [a;b] và m ≤ f(x) ≤ M, ∀ x ∈ [a;b] thì

$m(b-a)\le {\int }_a^{b}f(x)dx\le M(b-a)$

B. Các phương pháp tính tích phân

1. Phương pháp đổi biến số

Định lý 1

Cho hàm số f(x) liên tục trên đoạn [a;b]. Giả sử hàm số x = φ(t) có đạo hàm liên tục trên đoạn [α;β] sao cho φ(α) = a;φ(β) = b và a ≤ φ(t) ≤ b với mọi t ∈ [α;β]. Khi đó:

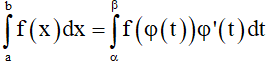
Từ định lý 1 ta rút ra các bước đổi biến số

1. Đặt x = φ(t), ta xác định đoạn [α;β] sao cho φ(α) = a;φ(β) = b và a ≤ φ(t) ≤ b, ∀t ∈ [α;β];

2. Biến đổi f(x)dx = f(φ(t))φ'(t)dt = g(t)dt

3. Tìm một nguyên hàm G(t) của g(t)

4. Tính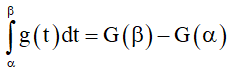 

5. Kết luận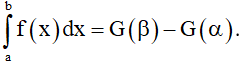

Định lý 2

Cho hàm số f(x) liên tục trên đoạn [a;b]. Nếu hàm số có u = u(x) đạo hàm liên tục trên đoạn [a;b] và a ≤ u(x) ≤ b với mọi x ∈ [a;b] sao cho f(x) = g(u(x))u'(x) , g(u) liên tục trên đoạn [α;β] thì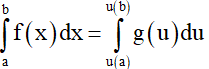 

Từ định lý 2 ta rút ra các bước đổi biến số

1. Đặt u = u(x),

2. Biến đổi f(x)dx = g(u)du.

3. Tìm một nguyên hàm G(u) của g(u) .

4. Tính .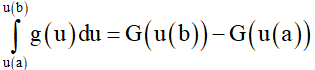

5. Kết luận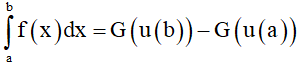 

2. Phương pháp tích phân từng phần

Tương tự tính nguyên hàm từng phần, ta có định lý sau: 

Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a;b] thì 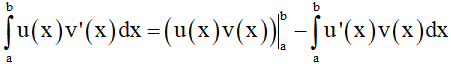hay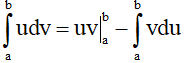 

hay .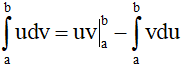

Một số cách đặt tích phân từng phần thường gặp với :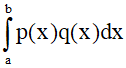

C. CÁC DẠNG TOÁN VÀ VÍ DỤ MINH HOẠ

1. Phương pháp đổi biến số

Dạng 1: Đổi biến số với các hàm vô tỉ quen thuộc

Phương pháp giải: Thực hiện theo các bước ở lý thuyết.

Chú ý:

- Trong biểu thức của f(x)dx có chứa căn thì đặt căn đó bằng t.

- Trong biểu thức của f(x)dx có chứa biểu thức lũy thừa bậc cao thì đặt biểu thức đó bằng t.

- Trong biểu thức của f(x)dx có chứa hàm mũ với biểu thức trên mũ là một hàm số thì đặt biểu thức trên mũ bằng t.

Ví dụ minh họa:

Ví dụ 1: Tính các tích phân sau bằng phương pháp đổi biến số:

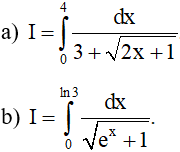
Lời giải

Chú ý: Đổi biến nhớ phải đổi cận.

a) Đặt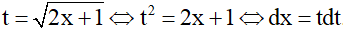  

Đổi cận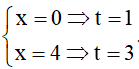 

Khi đó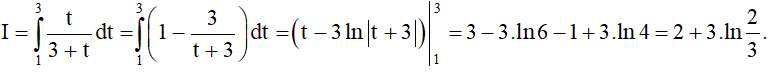 

b) Đặt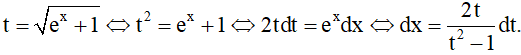 

Đổi cận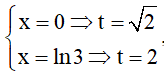khi đó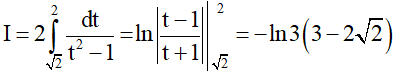 

Dạng 2: Tích phân đổi biến số với hàm ẩn

Phương pháp giải: Thực hiện theo các bước ở lý thuyết.

Chú ý tính chất: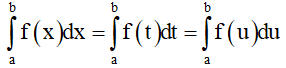(tích phân không phụ thuộc vào biến).

Ví dụ minh họa: 

Ví dụ 2: Cho hàm số f(x) liên tục trên R thỏa mãn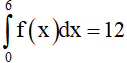

Tính tích phân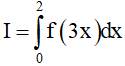

A. I = 6                   B. I = 36

C. I = 2                   D. I = 4

Lời giải

Ta có: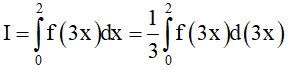 

Đổi biến: Đặt t = 3x => dt = 3dx

Đổi cận: x = 0 thì t = 0; x = 2 thì t = 3.2 = 6 

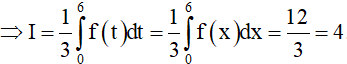(tích phân không phụ thuộc vào biến)

Chọn D

Dạng 3: Tích phân đổi biến số với hàm số chẵn, hàm số lẻ

Bài toán tổng quát: Giả sử hàm số f(x) liên tục trên đoạn [-a; a]. Chứng minh rằng:

a) 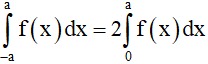 nếu f(x) là hàm số chẵn.

b) 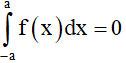 nếu f(x) là hàm số lẻ.

Phương pháp giải

a) Hàm số f(x) là hàm chẵn thì

Ta có: 

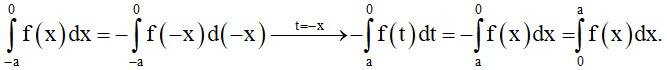
Do đó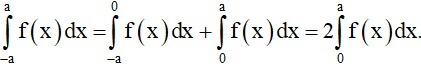  

b) Hàm số f(x) là hàm lẻ thì f(-x) = f(x)

Ta có: 

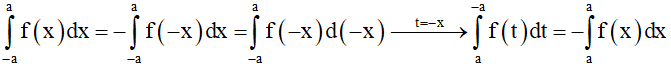
Do đó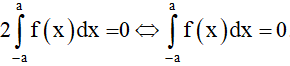 

Ví dụ minh họa 

Ví dụ 3: Cho hàm số y = f(x) liên tục trên đoạn [0; 1] thỏa mãn f(x) + 2f(1 - x) = 3x, ∀x ∈ R

Tính tích phân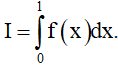 

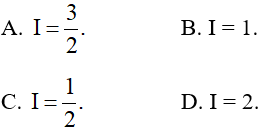
Lời giải

Cách 1: Ta có f(x) + 2f(1 - x) = 3x

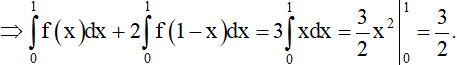
Đặt t = 1 - x => dt = - dx =>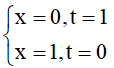 

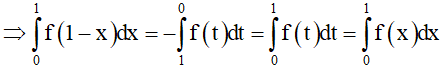
Suy ra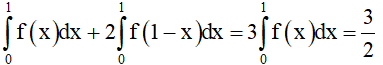 

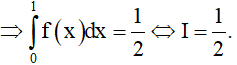
Chọn C.

Cách 2: Ta có f(x) + 2f(1 - x) = 3x 

=> f(1 - x) +2f(x) = 3(1 - x) = 3 - 3x

Khi đó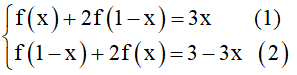 

Lấy 2.(2) - (1) ta được 3f(x) = 2(3 - 3x) - 3x <=> f(x) = 2 - 3x

Vậy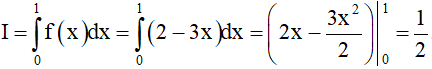 

Chọn C.

Dạng 4. Tích phân hàm phân thức hữu tỉ

Phương pháp giải: Thực hiện theo các bước ở lý thuyết.

Chú ý: Cách phân tích hàm phân thức hữu tỉ (giống phần nguyên hàm): Sử dụng phương pháp đồng nhất hệ số để phân tích.

Ví dụ minh họa

Ví dụ 4. Tính tích phân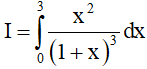 

Lời giải

Đặt 1 + x = u => dx = du

Đổi cận x = 0; u = 1; x = 3 => u = 4;

Khi đó

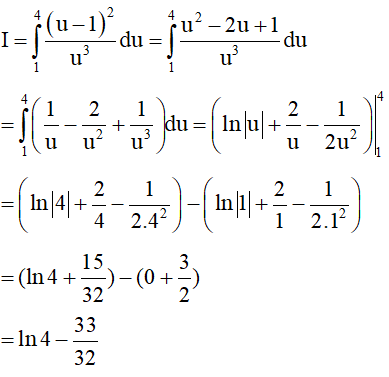
Chọn D.

2. Phương pháp tích phân từng phần

Phương pháp giải: Sử dụng công thức tích phân từng phần 

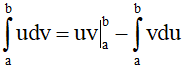
Chú ý: Cách chọn u, v (theo bảng đã cho ở phần lý thuyết)

Ví dụ minh họa

Ví dụ 1: Cho tích phân 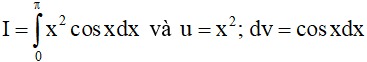 K.hẳng định nào sau đây đúng?

Lời giải

Ta có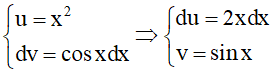 

Theo công thức tích phân từng phần: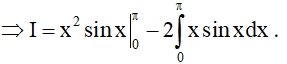  

Chọn D.

Ví dụ 2: Cho tích phân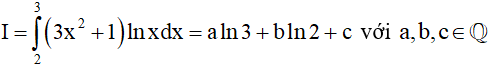.Khẳng định nào dưới đây là khẳng định đúng?

A. a = 3b.

B. a = – 3b.

C. a + b = 40.

D. a – b = 20.

Lời giải

Đặt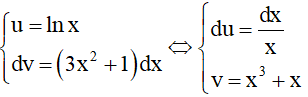 

Theo công thức tích phân từng phần 

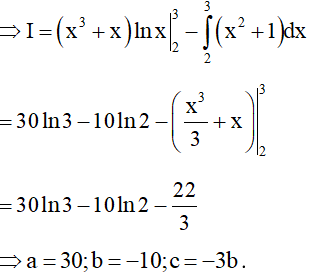
 Chọn B.

Ví dụ 3. Cho với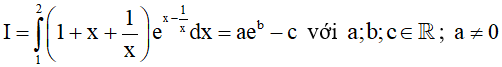Lúc này S = a + b + c có giá trị bằng

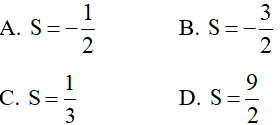
Lời giải

Ta có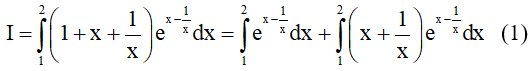

Đặt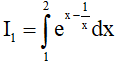

Đặt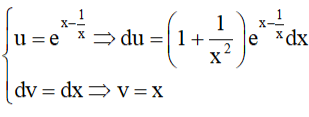 

Theo công thức tích phân từng phần ta có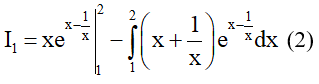

Từ (1); (2) ta có

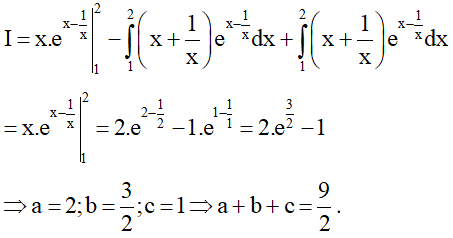
Chọn D.

D. BÀI TẬP TỰ LUYỆN

Câu 1. Cho hàm số f liên tục trên R và hai số thực a < b. Nếu 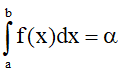 thì tích phân  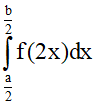có giá trị bằng

Câu 2. Bài toán tính tích phân 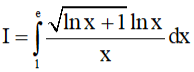 được một học sinh giải theo ba bước sau:

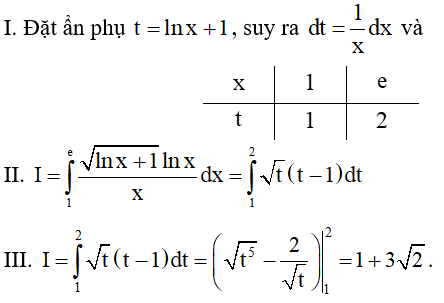
Học sinh này giải đúng hay sai? Nếu sai thì sai từ bước nào?

A. Bài giải đúng.

B. Sai từ Bước II.

C. Sai từ Bước I.

D. Sai ở Bước III.

Câu 3. Bài toán tính tích phân 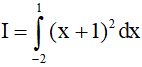 được một học sinh giải theo ba bước sau:

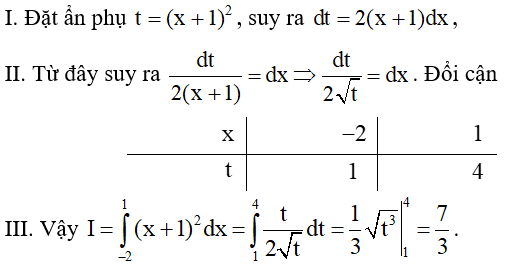
Học sinh này giải đúng hay sai? Nếu sai thì sai từ bước nào?

A. Sai từ Bước I.

B. Sai ở Bước III. 

C. Sai từ Bước II.

D. Bài giải đúng.

Câu 4. Cho tích phân: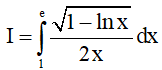 .Đặt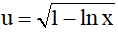.Khi đó I bằng

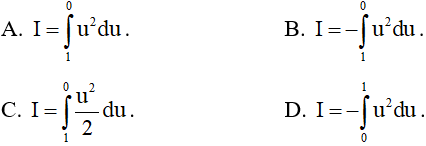
Câu 5. Tích phân 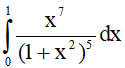 bằng

Câu 6. Tích phân 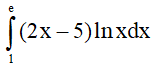 bằng

Câu 7. Tìm m để ?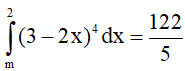

A. 0.                     B. 9.

C. 7.                     D. 2.

Câu 8. Tích phân 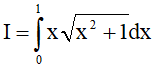 có giá trị là

Câu 9. Giá trị của tích phân 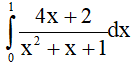 là

A. ln2.                   B. ln3.

C. 2ln2.                 D. 2ln3.

Câu 10. Giá trị của tích phân 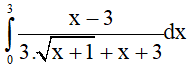 là

Câu 11. Giá trị của tích phân 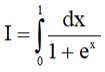 là

Câu 12. Giá trị của tích phân 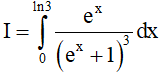 là

Câu 13. Giá trị của tích phân 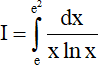 là

A. 2ln3.                   B. ln3.

C. ln2.                     D. 2ln2.

Câu 14. Giá trị của tích phân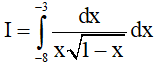là

Câu 15. Biết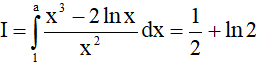. Giá trị của  là

A. 2.                        B. ln2.                     

C. π.                       D. 3.

Câu 16. Kết quả phép tính tích phân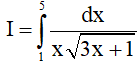có dạng I = aln3 + bln5 (a,b ∈ Z). Khi đó a² + ab + 3b² có giá trị là

A. 1.                        B. 5.

C. 0.                        D. 4.

Câu 17. Biết rằng 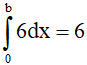 và 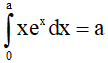. Khi đó biểu thức b² + a³ + 3a² + 2a có giá trị bằng

A. 5.                        B. 4.

C. 7.                        D. 3.

Câu 18. Giả sử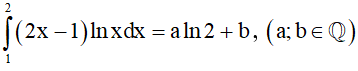Tính a + b.

Câu 19. Biết rằng 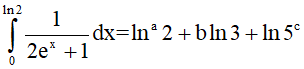. Trong đó a, b, c là các số nguyên. Khi đó S = a + b – c bằng bao nhiêu.

A. S = 4.                  B. S = 3.

C. S = 5.                  D. S = 2.

Câu 20. Cho hàm số y = f(x) là hàm lẻ và liên tục trên [-4;4], biết 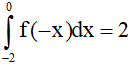 và 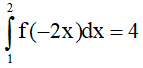. Tính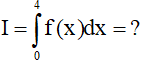 

A. -10.                     B. -6.

C. 6.                        D. 10.

Đáp án

1	2	3	4	5	6	7	8	9	10
A	D	C	B	A	C	A	B	D	C
11	12	13	14	15	16	17	18	19	20
A	B	C	A	A	B	C	D	B	B