Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tóm tắt lý thuyết và bài tập trắc nghiệm véctơ trong không gian, quan hệ vuông góc, tài liệu bao gồm 29 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

A. LÝ THUYẾT CƠ BẢN

I - Véctơ trong không gian

1. Định nghĩa:

Véctơ trong không gian là một đoạn thẳng có hướng. Kí hiệu $\overrightarrow{AB}$ chỉ véctơ có điểm đầu $A$, điểm cuối $B$. Véctơ còn đc kí hiệu là $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$,...

2. Các quy tắc về véctơ

- Quy tắc 3 điểm: $\overrightarrow{AC}$ = $\overrightarrow{AB}$ + $\overrightarrow{BC}$.

                 Hoặc: $\overrightarrow{AC}$ = $\overrightarrow{BC}$ + $\overrightarrow{AB}$.

- Quy tắc hình bình hành: cho hình bình hành $ABCD$: $\overrightarrow{AC}$ = $\overrightarrow{AB}$ + $\overrightarrow{AD}$.

- Quy tắc trung tuyến: $AM$ là trung tuyến của tam giác $ABC$ thì: $\overrightarrow{AM}$ = $\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC}).$

- Quy tắc trọng tâm: $G$ là trọng tâm tam giác $ABC$ thì: $\overrightarrow{GA}$ + $\overrightarrow{GB}$ + $\overrightarrow{GC}$ = $\overrightarrow{0}$.

- Quy tắc hình hộp: cho hình hộp $ABCD.A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ thì: $\overrightarrow{AB}$ + $\overrightarrow{AD}$ + $\overrightarrow{A{A}^{\prime }}$ = $\overrightarrow{A{C}^{\prime }}$.

3. Sự đồng phẳng của các véctơ, điều kiện để ba véctơ đồng phẳng

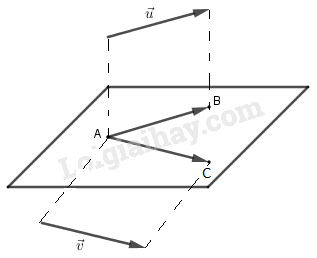
    Định nghĩa: ba véctơ gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.

    Điều kiện để ba véctơ đồng phẳng:

    Định lí 1: cho ba véctơ $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$, trong đó véctơ  $\overrightarrow{a}$, $\overrightarrow{b}$ không cùng phương. Điều kiện cần và đủ để ba véctơ $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ đồng phẳng là có các số $m,n$ sao cho $\overrightarrow{c}$ = $m\overrightarrow{a}$ + $n\overrightarrow{b}$. Hơn nữa các số $m,n$ là duy nhất.

    Định lí 2: nếu $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$,  là ba véctơ không đồng phẳng thì với mỗi véctơ $\overrightarrow{d}$ ta tìm được các số $m,n,p$ sao cho $\overrightarrow{d}$ = $m\overrightarrow{a}$ + $n\overrightarrow{b}$ + $p\overrightarrow{c}$. Hơn nữa các số $m,n,p$ là duy nhất.

II - Quan hệ vuông góc trong không gian

1. Hai đường thẳng vuông góc

1.1. Tích vô hướng của hai vectơ trong không gian.

  - Góc giữa hai véctơ trong không gian:

  Góc giữa hai vectơ (khác véctơ không) $\overrightarrow{u},\overrightarrow{v}$ là góc $\widehat{BAC}$ với $\overrightarrow{AB}=\overrightarrow{u}$; $\overrightarrow{AC}=\overrightarrow{v}$

- Tích vô hướng của hai vectơ trong không gian: 

Cho hai vectơ khác vectơ không $\overrightarrow{u},\overrightarrow{v}$ :

Biểu thức $\overrightarrow{u}.\overrightarrow{v}=|\overrightarrow{u}|.|\overrightarrow{v}|.cos(\overrightarrow{u},\overrightarrow{v})$ được gọi là tích vô hướng của hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$

Nếu $\overrightarrow{u}$ = $\overrightarrow{0}$ hoặc $\overrightarrow{v}$ = $\overrightarrow{0}$ thì ta quy ước $\overrightarrow{u}$ . $\overrightarrow{v}$ = $\overrightarrow{0}$.

1.2. Vectơ chỉ phương của đường thẳng. 

  - Vectơ $\overrightarrow{a}\ne \overrightarrow{0}$ là véctơ chỉ phương của đường thẳng $d$ nếu giá của $\overrightarrow{a}$ song song hoặc trùng với $d$.

  - Nếu $\overrightarrow{a}$ là vectơ chỉ phương của đường thẳng $d$ thì k$\overrightarrow{a}$  ($k\ne 0$) cũng là vectơ chỉ phương của d.

 1.3. Góc giữa hai đường thẳng trong không gian. 

  Định nghĩa:

  Góc giữa hai đường thẳng $a$ và $b$ trong không gian là góc giữa hai đường thẳng $a^{\prime }$ và $b^{\prime }$ cùng đi qua một điểm và lần lượt song song với $a$ và $b$

  Nhận xét:

  - Ta có thể lấy điểm $O$ thuộc một trong hai đường thẳng $a$ và $b$, rồi vẽ một đường thẳng qua $O$ và song song với đường thẳng còn lại.

  - Nếu $\overrightarrow{u_1},\overrightarrow{u_2}$ lần lượt là vectơ chỉ phương của $a$ và $b$ và ($\overrightarrow{u_1},\overrightarrow{u_2})=\alpha$ thì:

    + góc $(a;b)=\alpha$  nếu $0^0\le \alpha \le {90}^0$

    + góc $(a;b)={180}^0-\alpha$ nếu ${90}^0<\alpha \le {180}^0$.

- Nếu $a//b$ hoặc $a\equiv b$ thì $\widehat{\left(a,b\right)}=0^0$

1.4. Hai đường thẳng vuông góc với nhau.

  a) Định nghĩa:

  Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng ${90}^0$

  b) Nhận xét:

  - Nếu$\overrightarrow{u_1},\overrightarrow{u_2}$ lần lượt là các VTCP của $a$ và $b$ thì: $a\perp b\iff \overrightarrow{u_1}.\overrightarrow{u_2}=0$.

  - Nếu  $\{\begin{array}{l}a//b\\ c\mathrm{\perp }a\end{array}$ thì $c\mathrm{\perp }b$

  - Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.

2. Đường thẳng vuông góc với mặt phẳng

2.1. Định nghĩa

    Một đường thẳng gọi là vuông góc với mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng ấy. 

    Định lí 1:

    Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì đường thẳng d vuông góc với mặt phẳng (P).

    Hệ quả: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc với cạnh thứ ba.

2.2. Tính chất

    Tính chất 1.

    Có duy nhất một mặt phẳng (P) đi qua một điểm O cho trước và vuông góc với một đường thẳng a cho trước.

    Mặt phẳng vuông góc với AB tại trung điểm O của đoạn AB, gọi là mặt phẳng trung trực của đoạn thẳng AB (h.3.26).

2.3. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng

    Tính chất 3.

    a) Mặt phẳng nào vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với đường thẳng còn lại.

    b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng song song với nhau.

    Tính chất 5.

    a) Cho đường thẳng a và mặt phẳng (P) song song với nhau. Đường thẳng nào vuông góc với (P) thì cũng vuông góc với a.

    b) Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.

2.4. Phép chiếu vuông góc

    Định nghĩa:

    Phép chiếu song song lên mặt phẳng (P) theo phương l vuông góc với mặt phẳng (P) gọi là phép chiếu vuông góc lên mặt phẳng (P).

    Định lí ba đường vuông góc:

    Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng b nằm trong (P). khi đó điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a' của a trên (P) (h.3.27).

2.5. Góc giữa đường thẳng và mặt phẳng

    Định nghĩa:

    Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa a và (P) bằng ${90}^0.$

    Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu a' của nó trên (P), gọi là góc giữa đường thẳng a và mặt phẳng (P) (h.3.28).

    Chú ý: góc giữa đường thẳng và mặt phẳng không vượt quá ${90}^0.$

3. Hai mặt phẳng vuông góc

3.1. Góc giữa hai mặt phẳng.

    Định nghĩa: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

    Cách xác định góc giữa hai mặt phẳng:

$(P)\cap (Q)=c$. Trong $(P)$ từ $I\in c$ vẽ $a\perp c$; trong $(Q)$ từ $I$ vẽ $b\perp c$. Góc giữa $a$ và $b$ là góc giữa $mp(P)$ và $mp(Q)$ (h.3.41).

    Diện tích hình chiếu của một đa giác.

    Cho đa giác $H$ thuộc $mp(Q)$. Gọi đa giác $H^{\prime }$ là hình chiếu của đa giác $H$ lên $mp(P)$; $\alpha =\widehat{(P;Q)}.$ Khi đó $S_{H^{\prime }}=S_H.cos\alpha .$

3.2. Hai mặt phẳng vuông góc 

    Định nghĩa: 

    Hai mặt phẳng gọi là vuông góc với nhau nếu góc giữa chúng bằng ${90}^0.$

    Định lý: Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

    Hệ quả 1

    Nếu hai mặt phẳng $(P)$ và $(Q)$ vuông góc với nhau thì bất cứ đường thẳng $a$ nào nằm trong mặt phẳng $(P)$, vuông góc với giao tuyến của $(P)$ và $(Q)$ đều vuông góc với mp $(Q)$.

     Hệ quả 2

     Nếu hai mặt phẳng $(P)$ và $(Q)$ vuông góc với nhau và $A$ là một điểm nằm trong $(P)$ thì đường thẳng $a$ đi qua điểm $A$ và vuông góc với $(Q)$ sẽ nằm trong $(P)$.

     Hệ quả 3

     Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.

3.3. Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương.

• Hình lăng trụ đứng là hình lăng trụ đứng có đáy là đa giác đều.
• Hình hộp đứng là hình lăng trụ đứng có đáy là hình bình hành.
• Hình hộp chữ nhật là hình hộp đứng có đấy là hình chữ nhật.
• Hình lập phương là hình hộp có tất cả các mặt là hình vuông.

3.4. Hình chóp đều và hình chóp cụt đều.

• Hình chóp đều:  

• • Một hình chóp được gọi là hình chóp đều nếu đáy của nó là 1 đa giác đều và đường cao của hình chóp đi qua tâm của đấy.
  • Hình chóp đều có các mặt cạnh bên tạo với mặt đáy các góc bằng nhau.

• Hình chóp cụt đều: Phần nằm giữa đáy và một thiết diện song song với đáy của hình chóp đều gọi là hình chóp cụt đều.

B. BÀI TẬP