Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Phương pháp xác định giao điểm – giao tuyến – thiết diện trong không gian, tài liệu bao gồm 17 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Phương pháp xác định giao điểm – giao tuyến – thiết diện trong không gian

Bài tập chương 2

Dạng 1 : Xác định giao tuyến của hai mặt phẳng \((\alpha )\) và \((\beta )\)

Phương pháp : 

-Tìm hai điểm chung phân biệt của hai mặt phẳng \((\alpha )\) và \((\beta )\)

- Đường thẳng đi qua hai điểm chung ấy là giao tuyến cần tìm

Chú ý : Để tìm chung của \((\alpha )\) và \((\beta )\) thường tìm 2 đường thẳng đồng phẳng lần lườt nằm trong hai mp giao điểm nếu có của hai đường thăng này là diểm chung của hai mặt phẳng

Bài tập

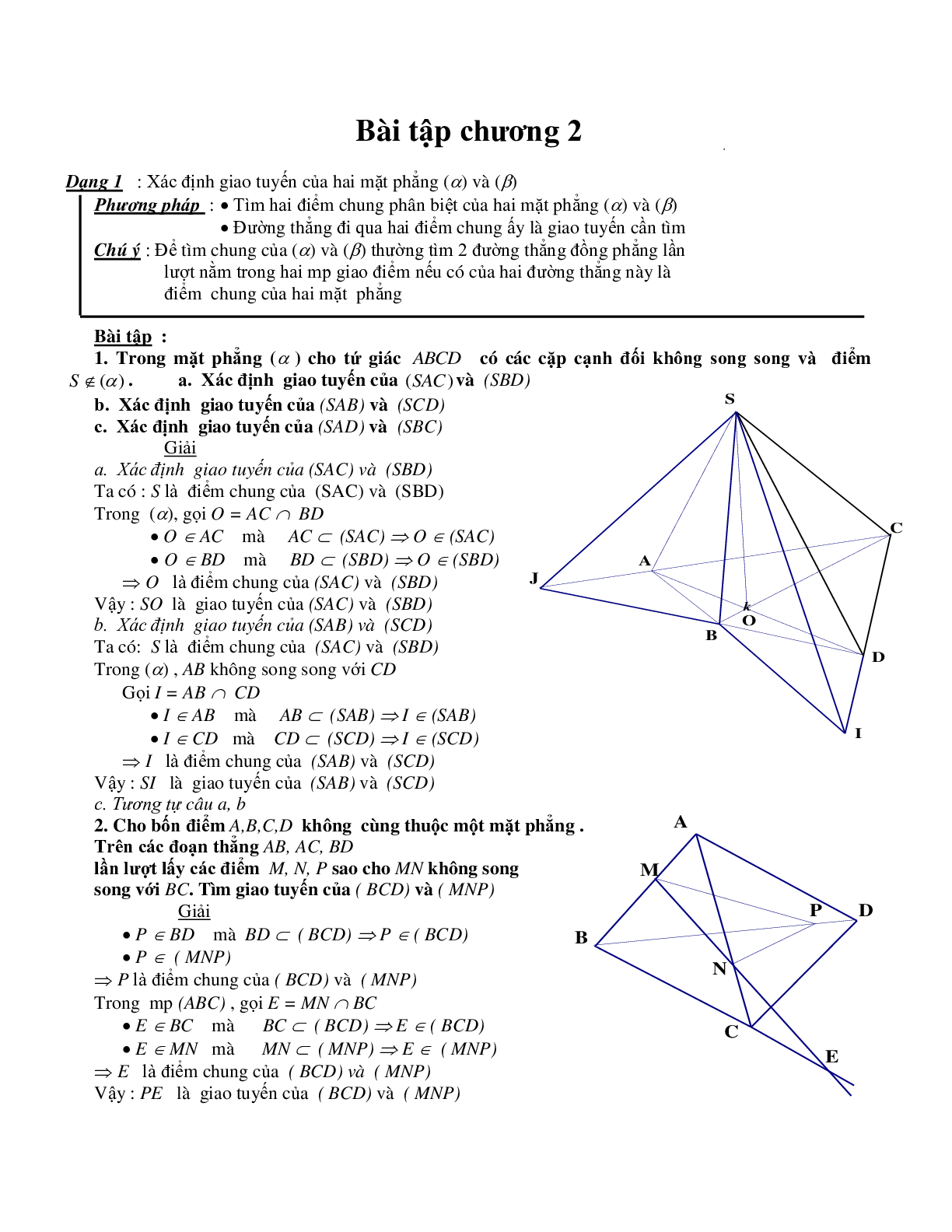
1. Trong mặt phẳng \((\alpha )\) cho tứ giác ABCD có các cặp cạnh đối không song song và điểm \(S \notin (\alpha )\).

a. Xác định giao tuyến của (SAC) và (SBD)

b. Xác định giao tuyến của (SAB) và (SCD)

c. Xác định giao tuyến của (SAD) và (SBC)

Giải

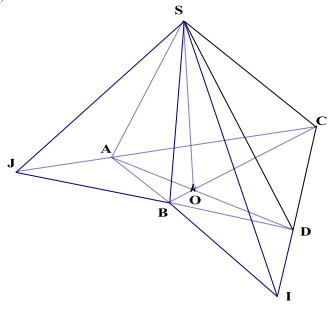
a. Xác định giao tuyến của (SAC) và (SBD)

Ta có : S là điểm chung của (SAC) và (SBD)

Trong \((\alpha )\), gọi \(O = AC \cap BD\)

- \(O \in AC\) mà \(AC \subset (SAC) \Rightarrow O \in (SAC)\)

- \(O \in BD\) mà \(BD \subset (SBD) \Rightarrow O \in (SBD)\)

\( \Rightarrow O\) là điểm chung của (SAC) và (SBD)

Vậy: SO là giao tuyến của (SAC) và (SBD)

b. Xác định giao tuyến của (SAB) và (SCD)

Ta có: S là điểm chung của (SAC) và (SBD)

Trong \((\alpha ),AB\) không song song với CD

Gọi \(I = AB \cap CD\)

- \(I \in AB\) mà \(AB \subset (SAB) \Rightarrow I \in (SAB)\)

- \(I \in CD\) mà \(CD \subset (SCD) \Rightarrow I \in (SCD)\)

\( \Rightarrow I\) là điểm chung của (SAB) và (SCD)

Vậy: SI là giao tuyến của (SAB) và (SCD)

c. Tương tự câu a, b

2. Cho bốn điểm A, B, C, D không cùng thuộc một mặt phẳng . Trên các đoạn thẳng AB, AC, BD lần lượt lấy các điểm M, N, P sao cho MN không song song với BC. Tìm giao tuyến của (BCD) và (MNP).

Giải

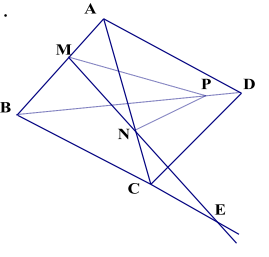
\( - P \in \underline {BD} \) mà \(BD \subset (BCD) \Rightarrow P \in (BCD)\)

- \(P \in (MNP)\)

\( \Rightarrow P\) là điểm chung của (BCD) và (MNP)

Trong \({\mathop{\rm mp}\nolimits} (ABC)\), gọi \(E = MN \cap BC\)

- \(E \in BC\) mà \(BC \subset (BCD) \Rightarrow E \in (BCD)\)

- \(E \in MN\) mà \(MN \subset (MNP) \Rightarrow E \in (MNP)\)

E là điểm chung của (BCD) và (MNP)

Vậy: PE là giao tuyến của (BCD) và (MNP)

3. Cho tam giác A B C và một điểm S không thuộc mp (ABC), một điểm I thuộc đoạn SA. Một đường thẳng a không song song với AC cắt các cạnh AB , BC theo thứ tự tại J, K.

Tìm giao tuyến của các cặp mp sau :

a. mp(I;a) và mp(SAC)

b. mp(I;a) và mp(SAB)

c. mp(I;a) và mp(SBC)

Giải

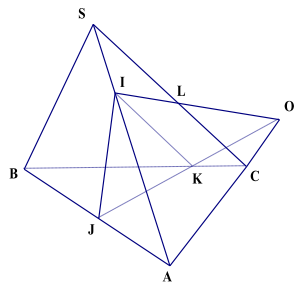
a. Tìm giao tuyến của mp(I;a) và mp(SAC) :

Ta có:

- \(I \in SA\) mà \(SA \subset (SAC) \Rightarrow I \in (SAC)\)

- \(I \in (I;a)\)

\( \Rightarrow I\) là điểm chung của hai mp(I;a) và mp(SAC)

Trong (ABC),a không song song với AC

Gọi \(O = a \cap AC\)

- \(O \in AC\) mà \(AC \subset (SAC) \Rightarrow O \in (SAC)\)

- \(O \in (I,a)\)

\( \Rightarrow O\) là điểm chung của hai mp(I;a) và mp(SAC)

Vậy: IO là giao tuyến của hai mp(I;a) và mp(SAC)

b. Tìm giao tuyến của mp (I;a) với mp (SAB) : là J I

c. Tìm giao tuyến của mp (I;a) với mp (SBC)

Ta có : K là điểm chung của hai mp (I;a) với mp (SBC)

Trong mp \((SAC)\), gọi \(L = IO \cap SC\)

- \(L \in SC\) mà \(\quad SC \subset (SBC) \Rightarrow L \in (SBC)\)

\( - L \in IO\) mà \(IO \subset (I,a) \Rightarrow L \in (I,a)\)

\( \Rightarrow L\) là điểm chung của hai mp (I;a) với mp (SBC)

Vậy: KL là giao tuyến của hai mp (I;a) với mp (SBC)

4. Cho bốn điểm A, B, C, D không cùng nằm trong một mp

a. Chứng minh AB và CD chéo nhau

b. Trên các đoạn thẳng AB và CD lần lưọt lấy các điểm M, N sao cho đường thẳng MN cắt đường thẳng BD tại I. Hỏi điểm I thuộc những mp nào . Xđ giao tuyến của hai mp (CMN) và (BCD)

Giải

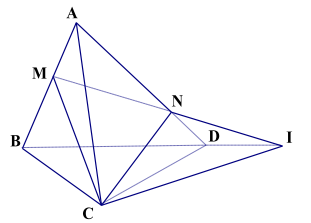
a. Chứng minh AB và CD chéo nhau:

Giả sử AB và CD không chéo nhau

Do đó có mp \((\alpha )\) chứa AB và CD

ABCD nằm trong \({\rm{mp}}(\alpha )\) mâu thuẩn giả thuyết

Vậy : AB và CD chéo nhau

b. Điểm I thuộc nhũng mp :

\( - I \in MN\) mà \(MN \subset (ABD) \Rightarrow I \in (ABD)\)

\( - I \in MN\) mà \(MN \subset (CMN) \Rightarrow I \in (CMN)\)

\( - I \in BD\), mà \(BD \subset (BCD) \Rightarrow I \in (BCD)\)

Xđ giao tuyến của hai mp(CMN) và (BCD) là CI

5. Cho tam giác ABC nằm trong mp(P) và a là mộtđường thẳng nằm trong mp(P) và không song song với AB và AC . S là một điểm ở ngoài mặt phẳng (P) và \(A\) ' là một điểm thuộc SA.

Xđ giao tuyến của các cặp mp sau

a. \({\bf{mp}}\left( {{A^\prime },a} \right)\) và \((SAB)\)

b. \({\mathop{\rm mp}\nolimits} \left( {{A^\prime },a} \right)\) và \((SAC)\)

c. \({\bf{mp}}\left( {{A^\prime },a} \right)\) và \((SBC)\)

Giải

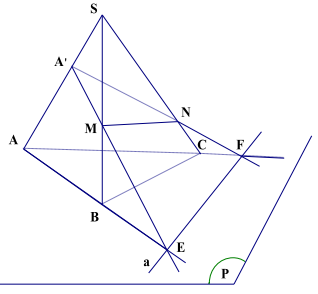
 a. Xđ giao tuyến của mp \(\left( {{A^\prime },a} \right)\) và \((SAB)\)

 - \({A^\prime } \in SA\) mà \[SA \subset (SAB) \Rightarrow A' \in (SAB)\]

- \({A^\prime } \in \left( {{A^\prime },a} \right)\)

\( \Rightarrow {A^\prime }\) là điểm chung của \(\left( {{A^\prime },a} \right)\) và (SAB)

Trong (P), ta có a không song song với AB

Gọi \(E = a \cap AB\)

- \(E \in AB\) mà \(AB \subset (SAB) \Rightarrow E \in (SAB)\)

- \(E \in \left( {{A^\prime },a} \right)\)

\( \Rightarrow E\) là điểm chung của \(\left( {{A^\prime },a} \right)\) và (SAB)

Vậy: \({A^\prime }E\) là giao tuyến của \(\left( {{A^\prime },a} \right)\) và (SAB)

b. Xđ̈ giao tuyến của mp \(\left( {{A^\prime },a} \right)\) và (SAC)

- \({A^\prime } \in SA\) mà \(SA \subset (SAC) \Rightarrow {A^\prime } \in (SAC)\)

- \({A^\prime } \in \left( {{A^\prime },a} \right)\)

\( \Rightarrow {A^\prime }\) là điểm chung của \(\left( {{A^\prime },a} \right)\) và (SAC)

Trong (P), ta có a không song song với AC

Gọi \(F = a \cap AC\)

\( - F \in AC\) mà \(AC \subset (SAC) \Rightarrow F \in \)

\( - E \in \left( {{A^\prime },a} \right)\)

=> F là điểm chung của \(\left( {{A^\prime },a} \right)\) và (SAC)

Vậy: \({A^\prime }F\) là giao tuyến của \(\left( {{A^\prime },a} \right)\) và (SAC)

c. Xđ̉ giao tuyến của \(\left( {{A^\prime },a} \right)\) và (SBC)

Trong (SAB), gọi \(M = SB \cap {A^\prime }E\)

\( - M \in SB\quad \) mà \(\quad SB \subset (SBC) \Rightarrow M \in (SBC)\)

\( - M \in {A^\prime }E\quad \) mà \(\quad {A^\prime }E \subset \left( {{A^\prime },a} \right) \Rightarrow M \in \left( {{A^\prime },a} \right)\)

=>M là điểm chung của mp \(\left( {{A^\prime },a} \right)\) và (SBC)

Trong (SAC), gọi \(N = SC \cap {A^\prime }F\)

- \(N \in SC\quad \) mà \(\quad SC \subset (SBC) \Rightarrow N \in (SBC)\)

- \(N \in {A^\prime }F\) mà \({A^\prime }F \subset \left( {{A^\prime },a} \right) \Rightarrow N \in \left( {{A^\prime },a} \right)\)

\( \Rightarrow N\) là điểm chung của \({\rm{mp}}\left( {{A^\prime },a} \right)\) và (SBC)

Vậy: MN là giao tuyến của \(\left( {{A^\prime },a} \right)\) và (SBC)

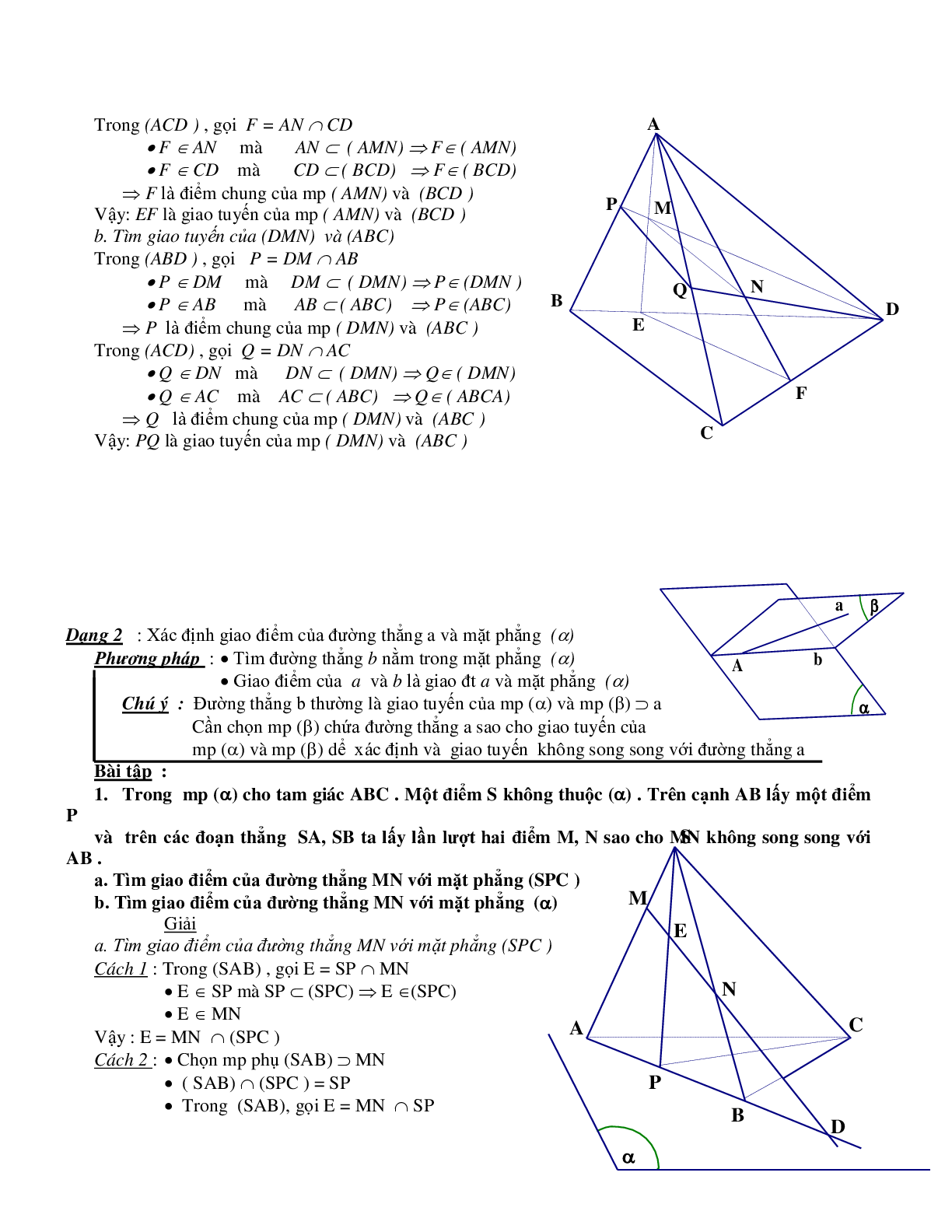
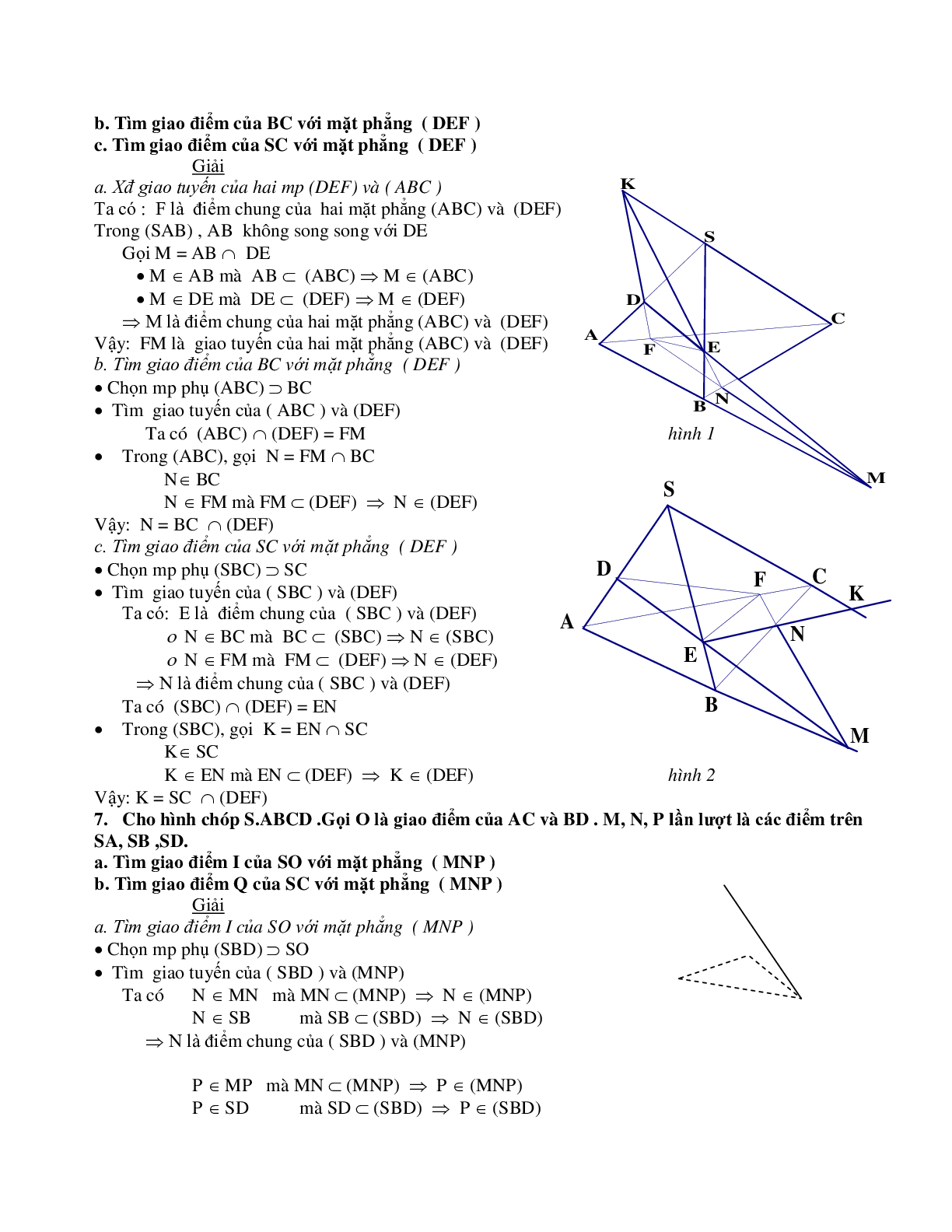
6. Cho tứ diện ABCD, M là một điểm bên trong tam giác A B D, N là một điểm bên trong tam giác ACD. Tìm giao tuyến của các cặp mp sau

a. (AMN) và (BCD)

b. (DMN) và (ABC)

Giải

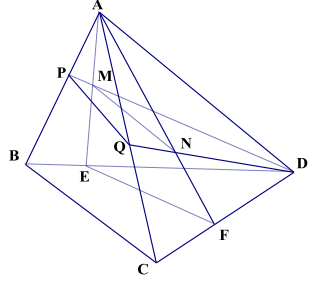
a. Tìm giao tuyến của (AMN) và (BCD)

Trong (ABD), gọi \(E = AM \cap BD\)

- \(E \in AM\) mà \(AM \subset (AMN) \Rightarrow E \in (AMN)\)

\( - E \in BD\) mà \(BD \subset (BCD) \Rightarrow E \in (BCD)\)

\( \Rightarrow E\) là điểm chung của mp(AMN) và (BCD)

Trong (ACD), gọi \(F = AN \cap CD\)

- \(F \in AN\quad \) mà \(\quad AN \subset (AMN) \Rightarrow F \in (AMN)\)

\( - F \in CD\) mà \(CD \subset (BCD) \Rightarrow F \in (BCD)\)

\( \Rightarrow F\) là điểm chung của mp(AMN) và (BCD)

Vậy: EF là giao tuyến của mp(AMN) và (BCD)

b. Tìm giao tuyến của (DMN) và (ABC)

Trong \((ABD)\), gọi \(P = DM \cap AB\)

- \(P \in DM\quad \) mà \(\quad DM \subset (DMN) \Rightarrow P \in (DMN)\)

- \(P \in AB\quad \) mà \(AB \subset (ABC) \Rightarrow P \in (ABC)\)

\( \Rightarrow P\) là điểm chung của mp (DMN) và (ABC)

Trong (ACD), gọi \({\rm{ }}Q = DN \cap AC\)

$\begin{array}{l}•Q\in DN\text{ ma }DN\subset \left(DMN\right)\Rightarrow Q\in \left(DMN\right)\\ •Q\in AC\text{ ma }AC\subset \left(ABC\right)\Rightarrow Q\in \left(ABCA\right)\end{array}$

=> Q là điểm chung của mp $\Rightarrow \left(DMN\right)\text{ va }\left(ABC\right)$

Vậy: PQ là giao tuyến của mp(DMN) và (ABC)

Dạng 2 : Xác định giao điểm của đường thẳng a và mặt phẳng \((\alpha )\)

Phương pháp :

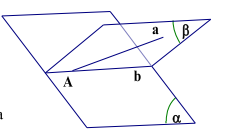
 -  Tìm đường thẳng b nằm trong mặt phẳng \((\alpha )\)

- Giao điểm của a và b là giao đt a và mặt phẳng \((\alpha )\)

Chú ý: Đường thẳng b thường là giao tuyến của \({\rm{mp}}(\alpha )\) và \({\rm{mp}}(\beta )\) để xác định và giao tuyến không song song với đường thẳng a

Bài tập:

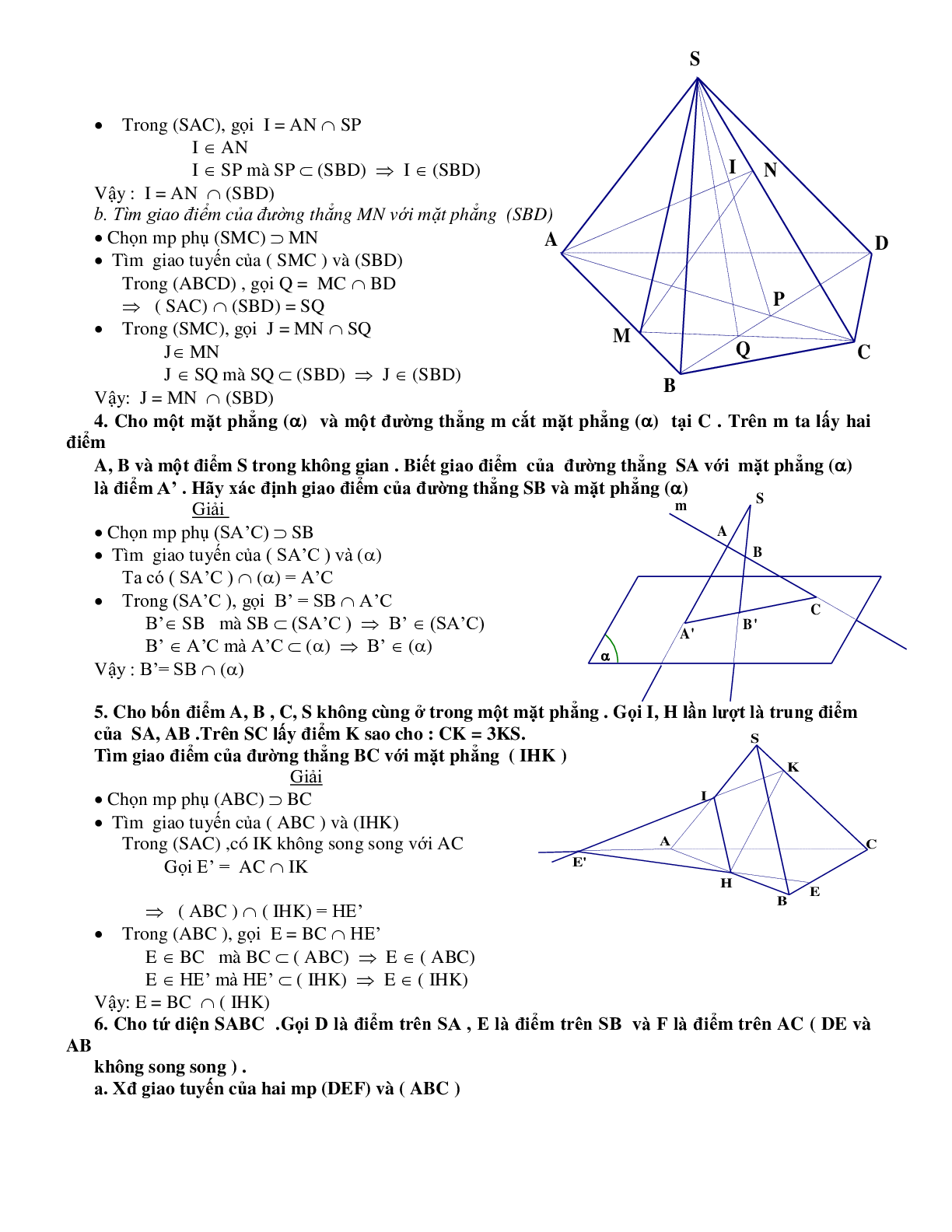
1. Trong \(mp(\alpha )\) cho tam giác ABC. Một điểm S không thuộc \((\alpha )\). Trên cạnh AB lấy một điểm P và trên các đoạn thẳng SA,SB ta lấy lần lưọt hai điểm M, N sao cho MON không song song với AB.

a. Tìm giao điểm của đường thẳng M N

b) Tìm giao điểm của đưởng thẳng MN với mặt phẳng \((\alpha )\)

Giải

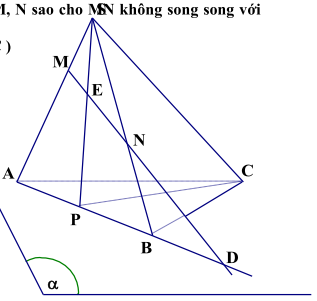
a. Tìm giao điểm của đường thẳng MN với mặt phẳng (SPC)

Cách 1 : Trong \(({\rm{SAB}})\), gọi \({\rm{E}} = {\rm{SP}} \cap {\rm{MN}}\)

- \({\rm{E}} \in {\rm{SP}}\) mà \({\rm{SP}} \subset ({\rm{SPC}}) \Rightarrow {\rm{E}} \in ({\rm{SPC}})\)

- \({\rm{E}} \in {\rm{MN}}\)

Vậy: \(E = MN \cap ({\rm{SPC}})\)

Cách 2:

- Chọn mp phụ (SAB) \( \supset {\rm{MN}}\)

- \(({\rm{SAB}}) \cap ({\rm{SPC}}) = {\rm{SP}}\)

- Trong (SAB), gọi \(E = MN \cap SP\)

\({\rm{E}} \in {\rm{MN}}\)

\({\rm{E}} \in {\rm{SP}}\) mà \({\rm{SP}} \subset ({\rm{SPC}})\)

Vậy: \({\rm{E}} = {\rm{MN}} \cap ({\rm{SPC}})\)

b. Tìm giao điểm của đường thẳng MN với \((\alpha )\)

Cách 1:  Trong (SAB), MN không song song với AB

Gọi \(D = AB \cap MN\)

- \({\rm{D}} \in {\rm{AB}}\) mà \({\rm{AB}} \subset (\alpha ) \Rightarrow {\rm{D}} \in (\alpha )\)

- \({\rm{D}} \in {\rm{MN}}\)

Vậy: \({\rm{D}} = {\rm{MN}} \cap (\alpha )\)

Cách 2:

- Chọn mp phụ \(({\rm{SAB}}) \supset {\rm{MN}}\)

- \(({\rm{SAB}}) \cap (\alpha ) = {\rm{AB}}\)

- Trong (SAB), MN không song song với AB

Gọi \({\rm{D}} = {\rm{MN}} \cap {\rm{AB}}\)

\({\rm{D}} \in {\rm{AB}}\) mà \({\rm{AB}} \subset (\alpha ) \Rightarrow {\rm{D}} \in (\alpha )\)

\({\rm{D}} \in {\rm{MN}}\)

Vậy: \(D = MN \cap (\alpha )\)

2. Cho tứ giác ABCD và một điểm S không thuộc mp (ABCD ). Trên đoạn SC lấy một điểm M không trùng với S và C. Tìm giao điểm của đường thẳng  SD với mặt phẳng (ABM)

Giải

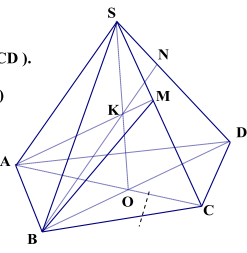
- Chọn mp phụ \(({\rm{SBD}}) \subset {\rm{SD}}\)

- Tìm giao tuyến của hai mp (SBD) và (ABM)

- Ta có \({\rm{B}}\) là điểm chung của (SBD) và (ABM)

- Tìm điểm chung thứ hai của (SBD) và (ABM)

Trong (ABCD), gọi \({\rm{O}} = {\rm{AC}} \cap {\rm{BD}}\)

Trong (SAC), gọi \({\rm{K}} = {\rm{AM}} \cap {\rm{SO}}\)

\({\rm{K}} \in {\rm{SO}}\) mà \({\rm{SO}} \subset ({\rm{SBD}}) \Rightarrow {\rm{K}} \in ({\rm{SBD}})\)

Vậy: \(N = SD \cap (ABM)\)

3. Cho tứ giác ABCD và một điểm S không thuộc mp (ABCD ). Trên đoạn AB lấy một điểm M, Trên đoạn SC lấy một điểm N(M,N không trùng với các đầu mút ).

a. Tìm giao điểm của đường thẳng AN với mặt phẳng (SBD)

b. Tìm giao điểm của đường thẳng MN với mặt phẳng (SBD)

Giải

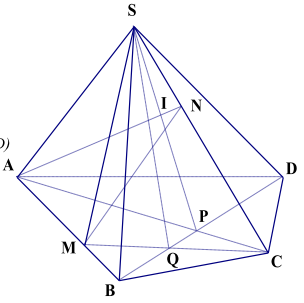
a. Tìm giao điểm của đường thẳng AN với mặt phẳng (SBD)

- Chọn mp phụ \(({\rm{SAC}}) \subset AN\)

- Tìm giao tuyến của (SAC) và (SBD)

- Trong (SAC), gọi \({\rm{I}} = {\rm{AN}} \cap {\rm{SP}}\)

\({\rm{I}} \in {\rm{AN}}\)

\({\rm{I}} \in {\rm{SP}}\) mà \({\rm{SP}} \subset ({\rm{SBD}}) \Rightarrow {\rm{I}} \in ({\rm{SBD}})\)

Vậy : I = AN \( \cap ({\rm{SBD}})\)

b. Tìm giao diểm của đường thẳng  MN với mặt phẳng (SBD)

- Chọn mp phụ \(({\rm{SMC}}) \subset MN\)

- Tìm giao tuyến của (SMC) và (SBD)

\( \Rightarrow ({\rm{SAC}}) \cap ({\rm{SBD}}) = {\rm{SQ}}\)

-  Trong (SMC), gọi \({\rm{J}} = {\rm{MN}} \cap {\rm{SQ}}\)

\({\rm{J}} \in {\rm{MN}}\)

\({\rm{J}} \in {\rm{SQ}}\) mà \({\rm{SQ}} \subset ({\rm{SBD}}) \Rightarrow {\rm{J}} \in ({\rm{SBD}})\)

Vậy: \({\rm{J}} = {\rm{MN}} \cap ({\rm{SBD}})\)