Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Phương pháp giải các dạng toán phép dời hình và phép đồng dạng trong mặt phẳng, tài liệu bao gồm 125 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Phương pháp giải các dạng toán phép dời hình và phép đồng dạng trong mặt phẳng

Chương I. Phép dời hình và phép đồng dạng trong mặt phẳng

Bài 1. Phép biến hình

A. Kiến thức cơ bản cần nắm

1. Định nghĩa

Đặt vấn đề: Trong mặt phẳng cho đường thẳng d và điểm M. Dựng hình chiếu vuông góc

M' của điểm M lên đường thẳng d.

Ta đã biết rằng với mỗi điểm M có một điểm \({{\rm{M}}^\prime }\) duy nhất là hình chiếu vuông góc của điểm M trên đường thẳng d cho trước (hình 1.1).

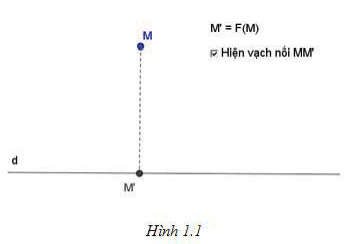
Ta có định nghĩa sau:

Định nghĩa: Quy tắc đặt tuoong ứng mỗi điểm M của măt phẳng với một điêm xác định duy nhất \({M^\prime }\) của mặt phẳng đó được gọi là phép biến hình trong mạt phẳng.

Nếu kí hiệu phép biến hình là F thì ta viết \(F(M) = {M^\prime }\) hay \({M^\prime } = F(M)\) và gọi điểm \({M^\prime }\) là ảnh của điểm M qua phép biến hình F.

Nếu H là một hình nào đó trong mặt phẳng thì ta kí hiệu \({{\rm{H}}^\prime } = {\rm{F}}({\rm{H}})\) là tập các điểm \({{\rm{M}}^\prime } = {\rm{F}}({\rm{M}})\), với mọi điểm M thuộc H. Khi đó ta nói F biến hình H thành hình \({{\rm{H}}^\prime }\), hay hình \({{\rm{H}}^\prime }\) là ảnh của hình H qua phép biến hình F.

Phép biến hình biến mỗi điểm M thành chính nó được gọi là phép đồng nhất.

2. Biểu thức tọa độ

GọiM(x;y) là điểm nằm trong mặt phẳng tọa độ Oxy, ta có: \({{\rm{M}}^\prime } = {\rm{f}}({\rm{M}})\).

Với M'(x';y') sao cho: \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = g(x;y)}\\{{y^\prime } = h(x;y)}\end{array}} \right.\)

Hệ (1) được gọi là biểu thức tọa độ của phép biến hình f.

3. Điểm bất động của phép biến hình

- Một điểm \(M \in (P)\) gọi là điểm bất động đối với phép biến hình \({\rm{f}}\) nếu \({\rm{f}}({\rm{M}}) = {\rm{M}}\).

Hình Học 11: Chương I-Phép dời hình và phép đồng dạng trong mặt phẳng

- Nếu f(M)=M với mọi điểm \({\rm{M}} \in ({\rm{P}})\) thì f được gọi là phép đồng nhất.

B. Phân dạng và phương pháp giải bài tập

Dạng 1. Xác định ảnh của một hình qua một phép biến hình

Phương pháp giải: Dùng định nghĩa hoặc biểu thức tọa độ của phép biến hình.

Ví dụ 1: Trong mặt phẳng tọa độ Oxy cho điểm M(1;-2), \({{\rm{M}}^\prime }\) là ảnh của M qua phép biến hình f có biểu thức tọa độ: \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = 2x + y - 1}\\{{y^\prime } = x - y + 2}\end{array}} \right.\). Tìm tọa độ \(\left( {{x^\prime };{y^\prime }} \right)\) của \({M^\prime }\).

Giải

Thay tọa độ điểm M vào biểu thức tọa độ của \({{\rm{M}}^\prime }\),

 ta được: \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}^\prime } = 2.1 + ( - 2) - 1 =  - 1}\\{{{\rm{y}}^\prime } = 1 - ( - 2) + 2 = 5}\end{array}} \right.\)

Vậy M' \(( - 1;5)\).

Ví dụ 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình \({\rm{x}} - {\rm{y}} + 1 = 0\). Tìm ảnh của đường thẳng d qua phép biến hình có biểu thức tọa độ là: \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = 2x - y}\\{{y^\prime } = 3x - 2y}\end{array}} \right.\).

Giải

Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = 2x - y}\\{{y^\prime } = 3x - 2y}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2{x^\prime } - {y^\prime }}\\{y = 3{x^\prime } - 2{y^\prime }}\end{array}\quad (*)} \right.} \right.\)

Thay (*) vào phương trình của d, ta được:

\(2{{\rm{x}}^\prime } - {{\rm{y}}^\prime } - 3{{\rm{x}}^\prime } + 2{{\rm{y}}^\prime } + 1 = 0 \Leftrightarrow {{\rm{x}}^\prime } - {{\rm{y}}^\prime } - 1 = 0\).

Do đó, phương trình của \({{\rm{d}}^\prime }\), ảnh của đường thẳng \({\rm{d}}\) là: \(x - y - 1 = 0\).

Dạng 2. Tìm điểm bất động của phép biến hình

Phương pháp giải: Dùng định nghĩa hoặc biểu thức tọa độ của phép biến hình.

Ví dụ: Trong mặt phẳng tọa độ Oxy cho phép biến hình f có biểu thức tọa độ là:

\(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = 2x + y - 1}\\{{y^\prime } = x + 2y - 1}\end{array}} \right.\). Tìm các điểm bất động của phép biến hình f.

Giải

M(x;y) là điểm bất động khi \({{\rm{M}}^\prime } = {\rm{f}}({\rm{M}}) = {\rm{M}}\).

Do đó, nếu \({{\rm{M}}^\prime }\left( {{{\rm{x}}^\prime };{{\rm{y}}^\prime }} \right)\) thì̀ \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}^\prime } = {\rm{x}}}\\{{{\rm{y}}^\prime } = {\rm{y}}}\end{array}} \right.\).

Thay vào biểu thức tọa độ, ta được:

\(\left\{ {\begin{array}{*{20}{l}}{x = 2x + y - 1}\\{y = x + 2y - 1}\end{array}} \right.\) hay \(x + y - 1 = 0\).

Vậy các điểm bất động của f nằm trên đường thẳng có phương trình \({\rm{x}} + {\rm{y}} - 1 = 0\).

C. Câu hỏi và bài tập trắc nghiệm khách quan

Câu 1. Gọi f là phép biến hình biến điểm M thành điểm \({M^\prime }\) được xác định bởi:

\(\overrightarrow {{\rm{O}}{{\rm{M}}^\prime }}  =  - \overrightarrow {{\rm{OM}}} \) với \({\rm{O}}\) là điểm cố định. Hỏi f có mấy điểm sao cho M=f(M)

A. Duy nhất 1 điểm

B. Ít nhất một

C. Ít nhất là hai

D. không có điểm nào

Hướng đẫn giải

Đáp án A

\({\rm{M}} = {\rm{f}}({\rm{M}}) \Leftrightarrow \overrightarrow {{\rm{OM}}}  =  - \overrightarrow {{\rm{OM}}}  \Leftrightarrow \overrightarrow {{\rm{OM}}}  = \vec 0 \Leftrightarrow {\rm{O}} \equiv {\rm{M}}\)

Vậy có duy nhất 1 điểm có ảnh là chính nó, đó là gốc tọa độ O.

Câu 2. Gọi f là phép biến hình biến điểm M thành điểm \({M^\prime }\) được xác định bởi \(\overrightarrow {{\rm{M}}{{\rm{M}}^\prime }}  = \overrightarrow {\rm{v}} (\overrightarrow {\rm{v}} \) là vectơ cho sắn khác \(\vec 0\) ). Hỏi điểm nào nằm trên đoạn thẳng AB có ảnh qua f là chính nó

A. A

B. B

C. trung điểm của AB

D. không có điểm nào

Hướng đẫn giải

Đáp án D

Gọi M thuộc đoạn thẳng AB có ảnh qua f là chính nó, ta có \({\rm{M}} = {\rm{f}}({\rm{M}}) \Leftrightarrow {\rm{ }}\overrightarrow {{\rm{M}}{{\rm{M}}^\prime }}  = \overrightarrow {\rm{v}} ( \ne \vec 0) \Leftrightarrow \)không có điểm M nào.

Câu 3. Cho đường thẳng \(\Delta \) cố định. Gọi f là phép biến hình biến điểm M thành điểm \({{\rm{M}}^\prime }\) sao cho \(\left\{ {\begin{array}{*{20}{l}}{{\rm{M}}{{\rm{M}}^\prime } \bot \Delta {\rm{ tai H}}}\\{{\rm{MH}} =  - \overrightarrow {{{\rm{M}}^\prime }{\rm{H}}} }\end{array}} \right.\) Giả sử \({{\rm{A}}^\prime } = {\rm{f}}({\rm{A}}),{{\rm{B}}^\prime } = {\rm{f}}({\rm{B}})\). Khẳng định nào sau đây đúng

A. \(AB > {A^\prime }{B^\prime }\)

B. \({\rm{AB}} < {{\rm{A}}^\prime }{{\rm{B}}^\prime }\)

C. \(AB = {A^\prime }{B^\prime }\)

D. Chỉ A đúng

Hướng dẫn giải

Đáp án C

Vì \({A^\prime } = f(A)\) và \({B^\prime } = f(B)\) nên \(\Delta \) là đường trụng trực của \(A{A^\prime }\) và \({B^\prime }\). Trong hình thang \({\rm{AB}}{{\rm{B}}^\prime }{{\rm{A}}^\prime }\), ta có \({{\rm{A}}^\prime }{{\rm{B}}^\prime } = {\rm{AB}}\).

Câu 4. Trong hệ trục tọa độ \({\rm{Oxy}},\overrightarrow {\rm{a}}  = (1;2);{\rm{M}}({\rm{x}},{\rm{y}});{{\rm{M}}^\prime }\left( {{{\rm{x}}^\prime },{{\rm{y}}^\prime }} \right)\). Biểu thức tọa độ của phép biến hình f biến \({\rm{M}}\) thành \({{\rm{M}}^\prime }\) sao cho \(\overrightarrow {{\rm{M}}{{\rm{M}}^\prime }}  = \overrightarrow {\rm{a}} \) có công thức nào sau đây:

A. \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x + 1}\\{{y^\prime } = y + 2}\end{array}} \right.\)

B. \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x - 1}\\{{y^\prime } = y - 2}\end{array}} \right.\)

C. \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x + 2}\\{{y^\prime } = y + 1}\end{array}} \right.\)

D. \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = y - 1}\\{{y^\prime } = x - 2}\end{array}} \right.\)

Hướng dẫn giải

Đáp án A

Vì \(\overrightarrow {{\rm{M}}{{\rm{M}}^\prime }}  = \overrightarrow {\rm{a}} \) nên \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}^\prime } = {\rm{x}} + 1}\\{{{\rm{y}}^\prime } = {\rm{y}} + 2}\end{array}} \right.\)

Câu 5. Trong hệ trục tọa độ Oxy, phép biến hình f biến M(x;y) thành \({{\rm{M}}^\prime }\left( {{{\rm{x}}^\prime },{{\rm{y}}^\prime }} \right)\) được xác định bởi \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x}\\{{y^\prime } = 2y}\end{array}} \right.\). Điểm nào sau đây có ảnh qua f là chính nó

A. (0;0)

B. (1;0)

C. (0;1)

D. \((x \in \mathbb{R},0)\)

Hướng dẫn giải

Đáp án D

M là ảnh qua f chính là \(M \Leftrightarrow M = f(M)\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = x}\\{y = 2y}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \in \mathbb{R}}\\{y = 0}\end{array}} \right.} \right.\)

Câu 6. Trong hệ trục tọa độ Oxy, phép biến hình f biến M(x;y) thành \({{\rm{M}}^\prime }\left( {{{\rm{x}}^\prime },{{\rm{y}}^\prime }} \right)\) được xác định bởi \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x}\\{{y^\prime } =  - y}\end{array}} \right.\). Ảnh của \(\Delta :x + y = 0\) qua f có phương trình là:

A. \(y = \frac{1}{2}x\)

B. (1;0)

C. (0;1)

D. \((x \in \mathbb{R},0)\)

Hướng dẫn giải

Đáp án C

Từ \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x}\\{{y^\prime } =  - y}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = {x^\prime }}\\{y =  - {y^\prime }}\end{array}} \right.} \right.\) thay vào \(x + y = 0\)

Ta có: \({x^\prime } - {y^\prime } = 0 \Leftrightarrow x - y = 0\)

Câu 7. Trong hệ trục tọa độ Oxy, phép biến hình f biến M(x;y) thành \({{\rm{M}}^\prime }\left( {{{\rm{x}}^\prime },{{\rm{y}}^\prime }} \right)\) được xác định bởi \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}^\prime } = {\rm{x}} - {\rm{y}}}\\{{{\rm{y}}^\prime } = {\rm{x}} + {\rm{y}}}\end{array}} \right.\). Gọi A(1;2) và B(-1;3). Tính độ dài của \({{\rm{A}}^\prime }{{\rm{B}}^\prime }\) ta được:

A. 10

B. 3

C. \(2\sqrt 3 \)

D. \(\sqrt {10} \)

Hướng dẫn giải

Đáp án D

Vì \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x - y}\\{{y^\prime } = x + y}\end{array}} \right.\) nên \({A^\prime }\) có tọa độ \(\left\{ {\begin{array}{*{20}{l}}{{x_{{A^\prime }}} = 1 - 2 =  - 1}\\{{y_{{A^\prime }}} = 2 + 1 = 3}\end{array}} \right.\)

Tương tự ta tìm được B(-4;2). Do đó: \({{\rm{A}}^\prime }{{\rm{B}}^\prime } = \sqrt {10} \)

Câu 8. Trong hệ trục tọa độ Oxy, phép biến hình f biến M(x;y) thành \({{\rm{M}}^\prime }\left( {{{\rm{x}}^\prime },{{\rm{y}}^\prime }} \right)\) được xác định bởi \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x}\\{{y^\prime } =  - 2y}\end{array}} \right.\).Ảnh của elip \((E):\frac{{{x^2}}}{2} + {y^2} = 1\) qua f là \(\left( {{E^\prime }} \right)\) có phương trình

A. \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{4} = 1\)

B. \(\frac{{{x^2}}}{4} + \frac{{{y^2}}}{1} = 1\)

C. \(\frac{{{x^2}}}{4} + 2{y^2} = 1\)

D. \({x^2} + \frac{{{y^2}}}{2} = 1\)

Hướng dẫn giải

Đáp án A

Vì \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x}\\{{y^\prime } =  - 2y}\end{array}} \right.\) nên \(\left\{ {\begin{array}{*{20}{l}}{x = {x^\prime }}\\{y =  - \frac{{{y^\prime }}}{2}}\end{array}} \right.\)

 thay vào \((E):\frac{{{x^2}}}{2} + {y^2} = 1\) ta được \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{4} = 1\)

Câu 9. Trong hệ trục tọa độ Oxy, phép biến hình f biến M(x;y) thành \({{\rm{M}}^\prime }\left( {{{\rm{x}}^\prime },{{\rm{y}}^\prime }} \right)\) được xác định bởi \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x}\\{{y^\prime } =  - 2y}\end{array}} \right.\). Ảnh của đường tròn \((C):{x^2} + {y^2} - 4 = 0\) qua f có phương trình

A. \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{4} = 1\)

B. \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{1} = 1\)

C. \({x^2} + 2{y^2} = 1\)

D. \({x^2} + \frac{{{y^2}}}{4} = 4\)

Hướng dẫn giải

Đáp án D

Vì \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x}\\{{y^\prime } =  - 2y}\end{array}} \right.\) nên \(\left\{ {\begin{array}{*{20}{l}}{x = {x^\prime }}\\{y =  - \frac{{{y^\prime }}}{2}}\end{array}} \right.\)

thay vào \((C):{x^2} + {y^2} - 4 = 0\) ta được \({x^2} + \frac{{{y^2}}}{4} = 4\)

Câu 10. Trong hệ trục tọa độ Oxy, phép biến hình f biến M(x;y) thành \({{\rm{M}}^\prime }\left( {{{\rm{x}}^\prime },{{\rm{y}}^\prime }} \right)\) được xác định bởi \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = 2x}\\{{y^\prime } = y}\end{array}} \right.\) Gọi \({M^{\prime \prime }}\left( {{x^{\prime \prime }},{y^{\prime \prime }}} \right)\) là ảnh của \({M^\prime }\) qua f. Tọa độ của \({M^{\prime \prime }}\) tính theo (x;y) của M là:

A. \(\left\{ {\begin{array}{*{20}{l}}{{x^{\prime \prime }} = 4x}\\{{y^{\prime \prime }} = y}\end{array}} \right.\)

B. \(\left\{ {\begin{array}{*{20}{l}}{{x^{\prime \prime }} = 2x}\\{{y^{\prime \prime }} = y}\end{array}} \right.\)

C. \(\left\{ {\begin{array}{*{20}{l}}{{x^{\prime \prime }} = x}\\{{y^{\prime \prime }} = y}\end{array}} \right.\)

D. \(\left\{ {\begin{array}{*{20}{l}}{{x^{\prime \prime }} = 3x}\\{{y^{\prime \prime }} = y}\end{array}} \right.\)

Hướng dẫn giải

Đáp án A

Vi \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = 2x}\\{{y^\prime } = y}\end{array}} \right.\) nên \(\left\{ {\begin{array}{*{20}{l}}{{x^{\prime \prime }} = 2{x^\prime }}\\{{y^{\prime \prime }} = {y^\prime }}\end{array}} \right.\).

 Suy ra: \(\left\{ {\begin{array}{*{20}{l}}{{x^{\prime \prime }} = 2(2x) = 4zx}\\{{y^{\prime \prime }} = y}\end{array}} \right.\)