Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Trắc nghiệm phép dời hình và phép đồng dạng trong các đề thi thử Toán 2018, tài liệu bao gồm 39 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Trắc nghiệm phép dời hình và phép đồng dạng trong các đề thi thử Toán 2018

Câu 1: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng  và \(\left( {{d_2}} \right):x - y - 2 = 0\). Có bao nhiêu phép tịnh tiến biến \({d_1}\) thành \({d_2}\).\(\left( {{d_1}} \right):2x + 3y + 1 = 0\)

A. Vô số.

B. 4 .

C. 1 .

D. 0 .

Chọn D

Lời giải

Nhắc lại kiến thức: "Phép tịnh tiến theo vectơ \(\vec v\) biến đường thẳng thành đường thẳng song song hoặc trùng với nó".

Ta có: \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) không song song hoặc trùng nhau, suy ra không có phép tịnh tiến nào biến đường thẳng \(\left( {{d_1}} \right)\) thành \(\left( {{d_2}} \right)\).

Câu 2: (THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018) Cho \(\vec v = ( - 1;5)\) và điểm \({M^\prime }(4;2)\). Biết \({M^\prime }\) là ảnh của M qua phép tịnh tiến \({T_{\vec v}}\). Tìm M.

A. M(-4;10).

B. M(-3;5).

C. M(3;7).

D. M(5; -3).

Lời giải

Chọn D

\(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x + a}\\{{y^\prime } = y + b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{4 = x - 1}\\{2 = y + 5}\end{array} \Rightarrow M(5; - 3)} \right.} \right.\)

Câu 3: (THPT Yên Lạc 2 – Vĩnh Phúc – lần 1 – năm 2017 – 2018) Cho điểm A’(1;4) và \(\vec u = ( - 2;3)\), biết \({A^\prime }\) là ảnh của A qua phép tịnh tiến \(\vec u\). Tìm tọa độ điểm A.

A. A(1;4).

B. A(-3;-1).

C. A(-1;-4).

D. A(3;1).

Lời giải

Chọn D

Gọi \(A(x;y)\).

Ta có \(\overrightarrow {A{A^\prime }}  = \vec u \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{1 - x =  - 2}\\{4 - y = 3}\end{array}} \right.\)

\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1 + 2 = 3}\\{y = 4 - 3 = 1}\end{array} \Rightarrow A(3;1)} \right.\).

Câu 4: (THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018) Cho hai đường thẳng song song d và \({d^\prime }\). Trong các khẳng định sau khẳng định nào đúng?

A. Có đúng một phép tịnh tiến biến d thành \({d^\prime }\).

B. Có vô số phép tịnh tiến biến d thành \({d^\prime }\).

C. Phép tịnh tiến theo véc tơ \(\vec v\) có giá vuông góc với đường thẳng d biến d thành \({d^\prime }\).

D. Cả ba khẳng định trên đều đúng.

Lời giải

Chọn B

Có vô số phép tịnh tiến véc tơ \(\vec v\) với điểm gốc nằm trên d và điểm ngọn nằm trên \({d^\prime }\) biến \(d\) thành \({d^\prime }\).

Câu 5: (THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018) Điểm M(-2;4) là ảnh của điểm nào sau đây qua phép tịnh tiến theo véctơ \(\vec v = ( - 1;7)\).

A. F(-1;-3).

B. P(-3;11).

C. E(3;1).

D. Q(1;3).

Lời giải

Chọn B

Gọi \({M^\prime }\left( {{x^\prime };{y^\prime }} \right)\) là ảnh của điểm M qua phép tịnh tiến theo véctơ \(\vec v = ( - 1;7)\).

Ta có \(\overrightarrow {M{M^\prime }}  = \left( {{x^\prime } + 2;{y^\prime } - 4} \right)\)

và \({T_{\bar v}}(M) = {M^\prime } \Leftrightarrow \overrightarrow {M{M^\prime }}  = \vec v\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^\prime } + 2 =  - 1}\\{{y^\prime } - 4 = 7}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^\prime } =  - 3}\\{{y^\prime } = 11}\end{array}} \right.} \right.\).

Câu 6: (THPT Hậu Lộc 2-Thanh Hóa- lần 1-năm 2017-2018) Hình nào sau đây có vô số trục đối xứng?

A. Hình vuông.

B. Hình tròn.

C. Đoạn thẳng.

D. Tam giác đều.

Lời giải

Chọn B

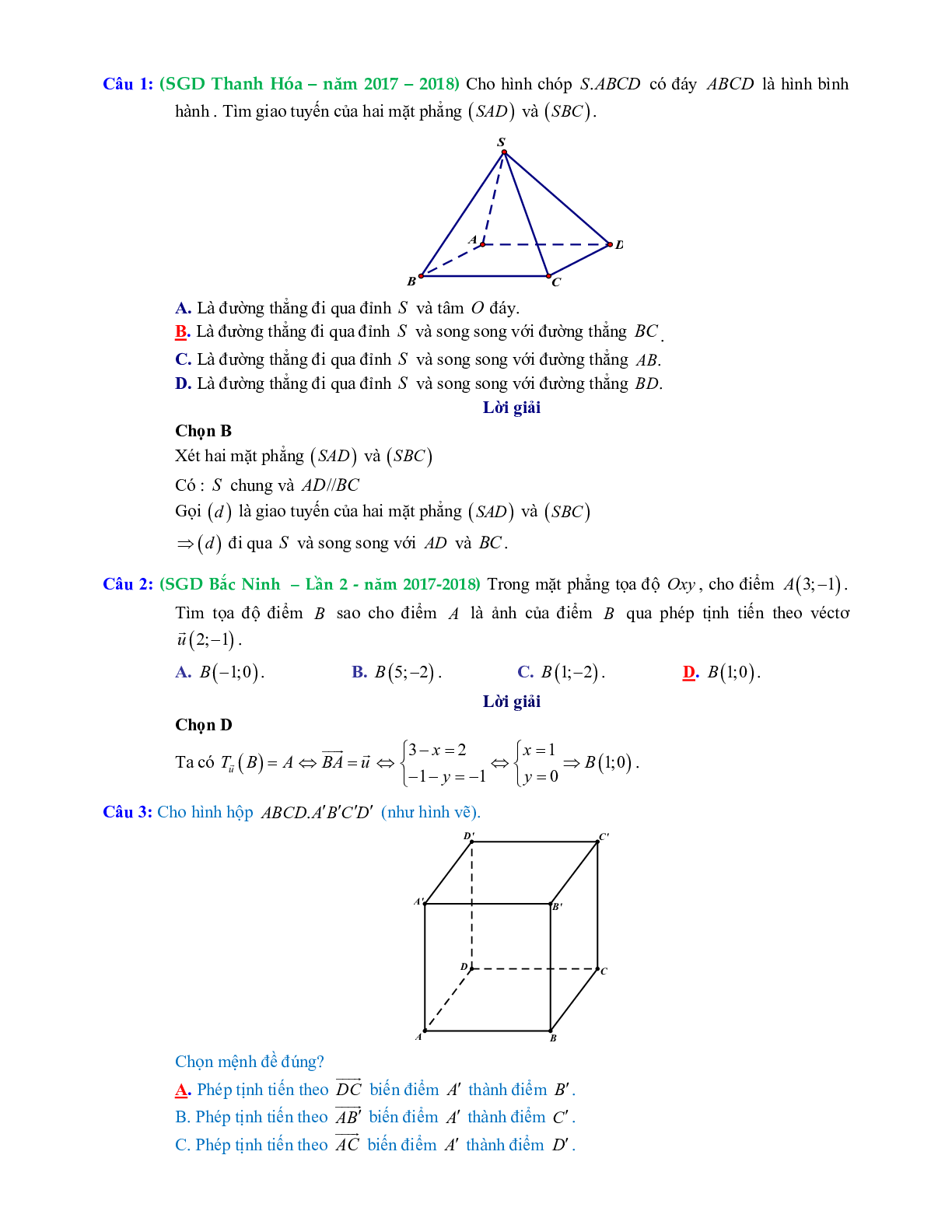
- Hình tròn có vô số trục đối xứng - là các đường thẳng đi qua tâm của đường tròn đó.

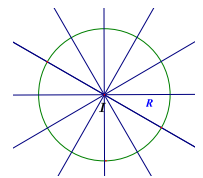
- Tam giác đều có 3 tục đối xứng như hình vẽ

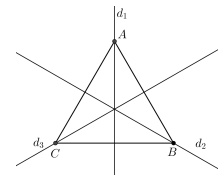
- Hình vuông có bốn trục đối xứng như hình vẽ

- Đoạn thẳng có hai trục đối xứng là đường thẳng đi qua 2 đầu đoạn thẳng và đường trung trực của đoạn thẳng đó.

Câu 7: (SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018) Trong mặt phẳng tọa độ Oxy, cho \(\vec v = ( - 2;3)\). Tìm ảnh của điểm A(1;-1) qua phép tịnh tiến theo vectơ \(\vec v\).

A. \({A^\prime }( - 2;1)\).

B. \({A^\prime }( - 1;2)\).

C. \({A^\prime }(2; - 1)\).

D. \({A^\prime }( - 1; - 2)\).

Lời giải

Chọn B

Giả sử \({A^\prime }(x;y)\).

 Theo công thức tọa độ của phép tịnh tiến ta có:

 \(\left\{ {\begin{array}{*{20}{l}}{x = 1 - 2}\\{y =  - 1 + 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x =  - 1}\\{y = 2}\end{array}} \right.} \right.\). Suy ra \({A^\prime }( - 1;2)\).

Câu 1: (THPT Triệu Sơn 1-lần 1 năm 2017-2018) Phép biến hình nào sau đây không là phép dời hình?

A. Phép tịnh tiến.

B. Phép đối xứng tâm.

C. Phép đối xứng trục.

D Phép vị tự.

Chọn D

Lời giải

Phép vị tự tâm I tỷ số k biến đoạn thẳng AB thành đoạn thẳng \({A^\prime }{B^\prime } = |k| \cdot AB\) nên nó không phải là phép dời hình với \(k \ne  \pm 1\).

Câu 2: (THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018) Cho hình bình hành ABCD. Ảnh của điểm D qua phép tịnh tiến theo véctơ \(\overrightarrow {AB} \) là:

A. B.

B. C.

C. D.

D. A.

Lời giải

Chọn B

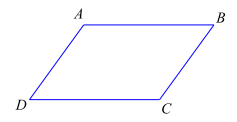
Ta có \(:\overrightarrow {AB}  = \overrightarrow {DC}  \Rightarrow {T_{\overrightarrow {AB} }}:D \to C\)

Thấy ngay phép tịnh tiến theo véctơ \(\overrightarrow {AB} \) biến điểm D thành điểm C vì \(\overrightarrow {AB}  = \overrightarrow {DC} \).

Câu 3: (THPT Triệu Thị Trinh-lần 1 năm 2017-2018) Cho hình thoi ABCD tâm O. Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Phép vị tự tâm O, tỉ số k = -1 biến tam giác ABD thành tam giác CDB.

B. Phép quay tâm O, góc \(\frac{\pi }{2}\) biến tam giác OBC thành tam giác OCD.

C. Phép vị tự tâm O, tỉ số k = 1 biến tam giác OBC thành tam giác ODA.

D. Phép tịnh tiến theo véc tơ \(\overrightarrow {AD} \) biến tam giác ABD thành tam giác DCB.

Lời giải

Chọn A

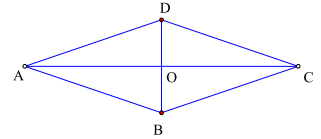
Ta có: \({V_{(O, - 1)}}(A) = C;{V_{(O, - 1)}}(B) = D;{V_{(O, - 1)}}(D) = B\). Nên chọn phương án A.

Câu 4: (THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018) Trong các khẳng định dưới đây, khẳng định nào sai?

A. Tam giác đều có ba trục đối xứng.

B. Phép quay biến một đường thẳng thành một đường thẳng song song với nó.

C. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.

D. Phép vị tự tâm I tỉ số k = -1 là phép đối xứng tâm.

Lời giải

Chọn B

Phép quay biến một đường thẳng thành một đường thẳng.

Câu 5: (SGD Bắc Ninh năm 2017-2018) Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M(2;5). Phép tịnh tiến theo vectơ \(\vec v = (1;2)\) biến điểm M\(M\) thành điểm \({M^\prime }\). Tọa độ điểm \({M^\prime }\) là:

A. \({M^\prime }(3;7)\).

B. \({M^\prime }(1;3)\).

C. \({M^\prime }(3;1)\).

D. \({M^\prime }(4;7)\).

Lời giải

Chọn A

Gọi \({T_{\bar v}}(M) = {M^\prime }\left( {{x^\prime };{y^\prime }} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^\prime } = 2 + 1 = 3}\\{{y^\prime } = 5 + 2 = 7}\end{array}} \right.\).

 Vậy \({M^\prime }(3;7)\).

Câu 6: (THPT Chuyên Hạ Long-Quảng Ninh-lần 1 năm 2017-2018) Hình nào dưới nào dưới đây không có trục đối xứng?

A. Tam giác cân.

B. Hình thang cân.

C. Hình elip.

D. Hình bình hành.

Hướng dẫn giải

Chọn D

Câu 7: (THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018) Trong mặt phẳng tọa độ Oxy, cho véctơ \(\vec v = ( - 3;5)\). Tìm ảnh của điểm A(1;2) qua phép tịnh tiến theo véctơ \(\vec v\)

A. \({A^\prime }(4; - 3)\).

B. \({A^\prime }( - 2;3)\).

C. \({A^\prime }( - 4;3)\).

D. \({A^\prime }( - 2;7)\).

Lời giải

Chọn D

Ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_{{A^\prime }}} = {x_A} + ( - 3) = 1 - 3 =  - 2}\\{{y_{{A^\prime }}} = {y_A} + 5 = 2 + 5 = 7}\end{array} \Rightarrow {A^\prime }( - 2;7).} \right.\)

Câu 8: (THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018) Cho hình chóp tam giác S.ABC với SA, SB, SC đôi một vuông góc và SA=SB=SC=a. Tính thế tích của khối chóp S.ABC.

A. \(\frac{1}{3}{a^3}\).

B. \(\frac{1}{2}{a^3}\).

C. \(\frac{1}{6}{a^3}\).

D. \(\frac{2}{3}{a^3}\).

Lời giải

Chọn C

Ta có \(V = \frac{1}{3} \cdot {S_{SBC}} \cdot SA = \frac{1}{3} \cdot \frac{1}{2} \cdot SB \cdot SC \cdot SA = \frac{1}{6} \cdot {a^3}\).

Câu 9: (THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018) Cho lăng trụ tam giác đều \(ABC.{A^\prime }{B^\prime }{C^\prime }\) có tất cả các cạnh bằng 2 a. Tính thể tích khối lăng trụ \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\).

A. \({a^3}\sqrt 3 \).

B. \(\frac{{{a^3}\sqrt 3 }}{4}\).

C. \(\frac{{{a^3}\sqrt 3 }}{2}\).

D. \(2{a^3}\sqrt 3 \).

Lời giải

Chọn \(C\)

Ta có \(V = {S_{ABC}} \cdot A{A^\prime } = \frac{{{{(2a)}^2}\sqrt 3 }}{4} \cdot 2a = 2{a^3}\sqrt 3 \).