Tailieumoi.vn xin giới thiệu chuyên đề Phép tịnh tiến thuộc chương trình Toán 11. Chuyên đề gồm 27 trang với đầy đủ lý thuyết, phương pháp giải các dạng bài tập và trên 200 bài tập có lời giải chi tiết từ cơ bản đến nâng cao giúp học sinh ôn luyện kiến thức, nâng cao kĩ năng làm bài tập môn Toán 11.
Chuyên đề Phép tịnh tiến
Phần 1: Dạng bài Tính chất của phép tịnh tiến hay, chi tiết
[1]. Định nghĩa
Trong mặt phẳng cho vectơ 
+) Phép biến hình biến mỗi điểm M thành điểm M'sao cho 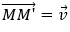

+) Phép tịnh tiến theo vectơ 
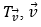
+) Như vậy:
(M’ được gọi là ảnh của điểm M)
Lưu ý: Phép tịnh tiến theo vectơ – không chính là phép đồng nhất.
[2]. Tính chất
* Tính chất 1:
Nhận xét: M'N' = MN.
* Tính chất 2: Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính.
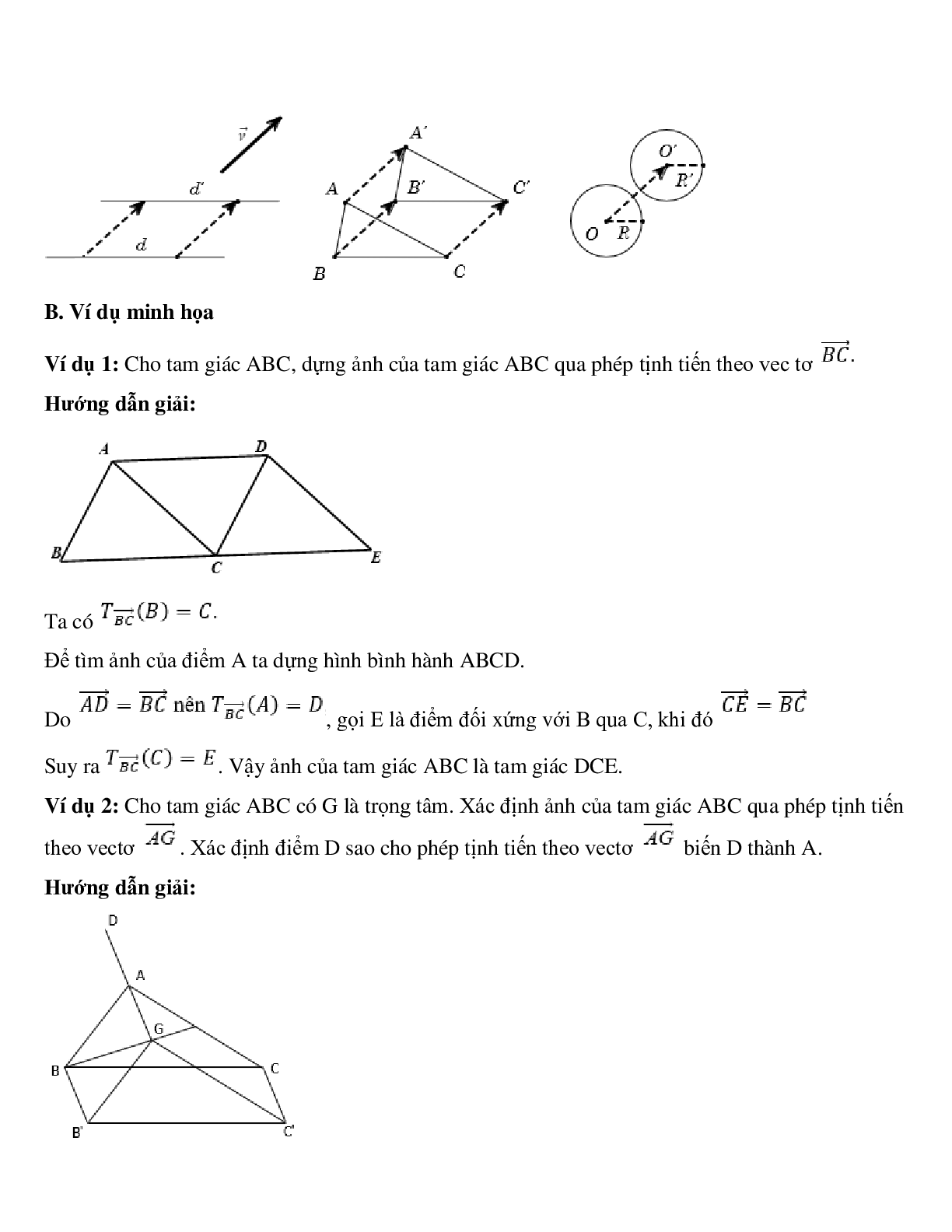
Ví dụ 1: Cho tam giác ABC, dựng ảnh của tam giác ABC qua phép tịnh tiến theo vec tơ
Hướng dẫn giải:
Ta có
Để tìm ảnh của điểm A ta dựng hình bình hành ABCD.
Do 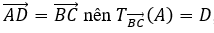
Suy ra 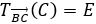
Ví dụ 2: Cho tam giác ABC có G là trọng tâm. Xác định ảnh của tam giác ABC qua phép tịnh tiến theo vectơ 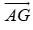
Hướng dẫn giải:
Ví dụ 3: Cho hình vuông ABCD tâm I. Gọi M,N lần lượt là trung điểm AD, DC. Tìm một Phép tịnh tiến biến tam giác AMI thành tam giá INC.
Hướng dẫn giải:
Vậy phép tịnh tiến theo 
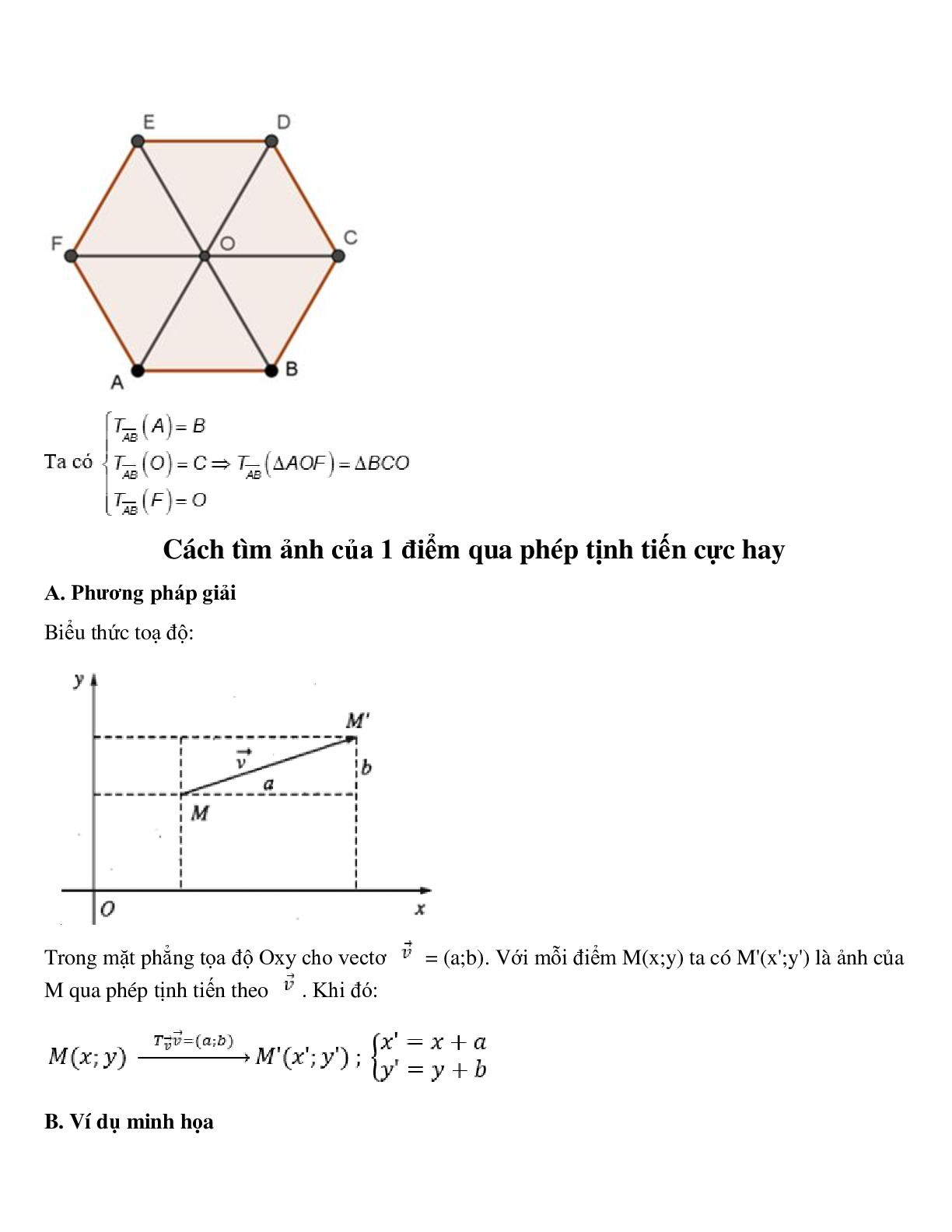
Ví dụ 4: Cho lục giác đều ABCDEF tâm O. Tìm ảnh của ∆AOF qua phép tịnh tiến theo vectơ 
Hướng dẫn giải:
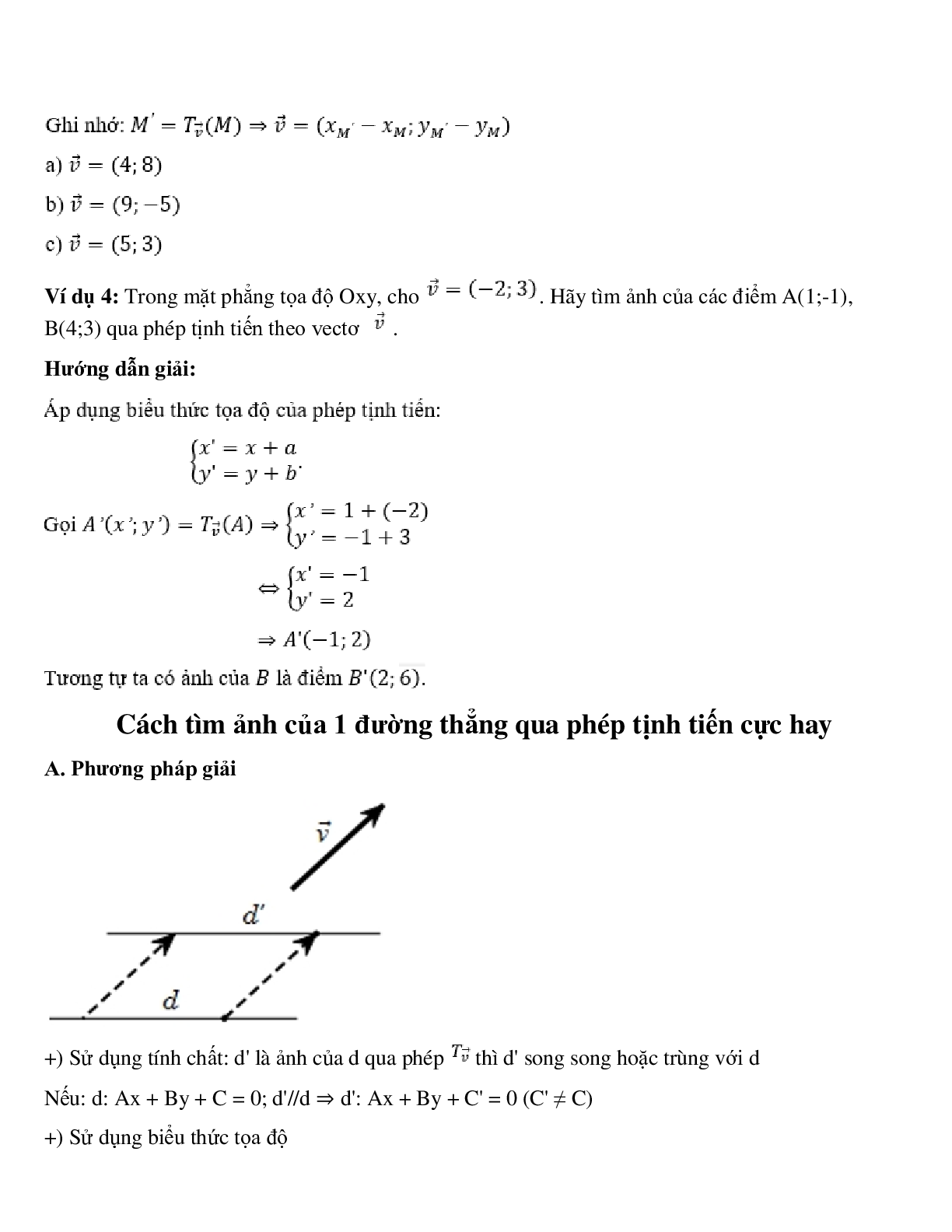
Phần 2: Cách tìm ảnh của 1 điểm qua phép tịnh tiến cực hay
Biểu thức toạ độ:
Trong mặt phẳng tọa độ Oxy cho vectơ 

Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho 

Hướng dẫn giải:
Áp dụng biểu thức tọa độ của phép tịnh tiến
Gọi
Tương tự ta có ảnh của B là điểm B'(2;6).
Ví dụ 2: Cho điểm A(1;4). Tìm tọa độ của điểm B sao cho 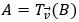
Hướng dẫn giải:
Ví dụ 3: Tìm tọa độ của vectơ 
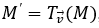
a) M(-1; 0), M'(3; 8)
b) M(-5; 2), M'(4; -3)
c) M(-1; 2), M'(4; 5)
Hướng dẫn giải:
Ví dụ 4: Trong mặt phẳng tọa độ Oxy, cho 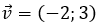

Hướng dẫn giải:
Phần 3: Cách tìm ảnh của 1 đường thẳng qua phép tịnh tiến cực hay
+) Sử dụng tính chất: d' là ảnh của d qua phép 
Nếu: d: Ax + By + C = 0; d'//d ⇒ d': Ax + By + C' = 0 (C' ≠ C)
+) Sử dụng biểu thức tọa độ
+) Chú ý:
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho 

Hướng dẫn giải:
Cách 1. Sử dụng biểu thức tọa độ của phép tịnh tiến.
Lấy điểm M(x;y) tùy ý thuộc d, ta có 2x - 3y + 5 = 0 (*)
Cách 2. Sử dụng tính chất của phép tịnh tiến
Do d' = 
Lấy điểm M(-1;1) ∈ d. Khi đó M' = 
Do M' ∈ d' ⇒ 2.0 - 3.(-2) + c = 0 ⇔ c = -6
Vậy ảnh của d là đường thẳng d': 2x - 3y - 6 = 0.
Cách 3. Để viết phương trình d' ta lấy hai điểm phân biệt M,N thuộc d, tìm tọa độ các ảnh M', N' tương ứng của chúng qua 
Cụ thể: Lấy M(-1;1), N(2;3) thuộc d, khi đó tọa độ các ảnh tương ứng là M'(0;-2), N'(3;0). Do d' đi qua hai điểm M', N' nên có phương trình
Ví dụ 2: Tìm PT đt d qua phép tịnh tiến theo 

Hướng dẫn giải:
* Cách 1: Gọi 
Chọn A’(2;-1) ∈ d’. Khi đó: 
Vậy: d: 2x + 3y – 8 = 0
* Cách 2: Chọn A’(2; -1) ∈ d’, 

Đt d đi qua 2 điểm A, B nên PT đt d là:
⇔ 2x – 8 = -3y
⇔ 2x + 3y – 8 = 0
* Cách 3: Gọi M’(x’;y’) ∈ d’, 
Ta có: M’ ∈ d’
⇔ 2x’ + 3y’ – 1 = 0
⇔ 2x – 4 + 3y – 3 – 1 = 0
⇔ 2x + 3y – 8 = 0
⇔ M ∈ d: 2x + 3y – 8 = 0
Ví dụ 3: Tìm tọa độ vectơ 

Hướng dẫn giải:
d' là ảnh của d qua phép 
Nhận thấy d//d’ nên với mỗi điểm A ∈ d; B ∈ d' ta có:
Ví dụ 4: Phép tịnh tiến theo vectơ 
Hướng dẫn giải:
Phần 4: Cách tìm ảnh của 1 đường tròn qua phép tịnh tiến cực hay
- Nhắc lại Phương trình đường tròn: Trong mặt phẳng Oxy, phương trình đường tròn có dạng:
+ Dạng 1: Đương tròn (C) tâm I (a;b), bán kính R, (C): (x - a)2 + (y - b)2 = R2
+ Dạng 2: (C): x2 + y2 - 2ax - 2by + c = 0 (điều kiện: a2 + b2 - c > 0) khi đó đường tròn tâm I (a;b) và bán kính
- Sử dụng tính chất: Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.
→ Như vậy, để viết phương trình (C’) ta chỉ cần tìm ảnh tâm I của (C) qua phép tịnh tiến.
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho đường tròn có phương trình (C): (x + 3)2 + (y – 1)2 = 4 với 

Hướng dẫn giải:
* Cách 1: (C) có tâm I(-3; 1) và bán kính R = 2
Khi đó: 

* Cách 2: Gọi M(x;y) ∈ (C),
Ta có: M ∈ (C) ⇔ (x’ + 3 + 3)2 + (y’ – 1 – 1)2 = 4 ⇔ M’ ∈ (C'): (x + 6)2 + (y – 2)2 = 4
Ví dụ 2: Trong mặt phẳng tọa độ Oxy ,Tìm ảnh của (C) qua phép tịnh tiến theo 

Hướng dẫn giải:
Cách 1. Sử dụng biểu thức tọa độ.
Lấy điểm M(x;y) tùy ý thuộc đường tròn (C), ta có x2 + y2 + 2x - 4y - 4 = 0 (*)
Gọi
Thay vào phương trình (*) ta được (x' - 2)2 + (y' + 3)2 + 2(x' - 2) - 4(y' + 3) - 4 = 0
⇔ x'2 + y'2 -2x' + 2y' - 7 = 0.
Vậy ảnh của (C) là đường tròn(C'): x2 + y2 - 2x + 2y - 7 = 0.
Cách 2. Sử dụng tính chất của phép tịnh tiến
Dễ thấy (C) có tâm I(-1;2) và bán kính r = 3. Gọi (C') = 
Ta có 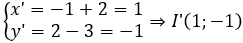
Ví dụ 3: Tìm tọa độ vectơ 

a) (C): (x – 2)2 + (y + 3)2 = 4 và (C’): (x + 5)2 + (y – 1)2 = 4
b) (C): x2 + y2 – 2x + 4y + 2 = 0 và (C’): x2 + y2 + 4x – 6y + 10 = 0
Hướng dẫn giải:
a) Từ (C), ta có: tâm I(2;-3) và từ (C’), ta có: tâm I’(-5; 1)
Khi đó: 

b) Từ (C), ta có: tâm I(1;-2) và từ (C’), ta có: tâm I’(-2; 3)
Khi đó: 

Chuyên đề : Phép biến hình trong mặt phẳng
Chủ đề 1: Phép tịnh tiến
I. Lý thuyết
1. Định nghĩa: Trong mặt phẳng cho vectơ \(\vec v\). Phép biến hình biến mỗi điểm M thành điểm \({M^\prime }\) sao cho: \(\overrightarrow {M{M^\prime }} = \vec v\), được gọi là phép tịnh tiến theo vecto \(\vec v\).
Ký hiệu : \({T_{\vec v}}\quad {T_{\vec v}}(M) = {M_0} \Leftrightarrow \overrightarrow {M{M_0}} = \vec v\)
2. Nhận xét: Phép tịnh tiến theo vecto không là phép đồng nhất
3. Biểu thức tọa độ
Cho \[\overrightarrow v = \left( {a{\rm{ }};{\rm{ }}b} \right)\] và phép tịnh tiến
\({T_{\vec v}}:\quad M(x;y) \mapsto {M^\prime } = {T_{\vec v}}(M) = \left( {{x^\prime };{y^\prime }} \right)\)
thì \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x + a}\\{{y^\prime } = y + b}\end{array}} \right.\)
4. Tính chất:
Tính chất 1 :
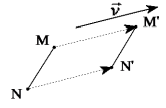
Nếu \({T_{\vec v}}(M) = {M^\prime },{T_{\vec v}}(N) = {N^\prime }\) thì \(\overrightarrow {MN} = \overrightarrow {{M^\prime }{N^\prime }} \) và từ đó suy ra: \({M^\prime }{N^\prime } = MN\).
Tính chất 2: Phép tịnh tiến:
1. Bảo toàn tính thẳng hàng và thứ tự của các điểm tương ứng.
2. Biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó.
3. Biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
4. Biến tam giác thành tam giác bằng nó.( trực tâm \( \to \) trực tâm, trọng tâm \( \to \) trọng tâm)
5. Biến đường tròn thành đương tròn có cùng bán kính ( \(\{ \begin{array}{*{20}{l}}{I \to {I^\prime }}\\{R = {R^\prime }}\end{array})\).

II. Bài tập tự luận minh họa
Bài tập 1: Cho điểm \(A(1;1),\Delta :x - 2y + 1 = 0,(C):{x^2} + {y^2} - 2x + 4y - 1 = 0\). Xác định tọa độ điểm \({A^\prime },{\Delta ^\prime },\left( {{C^\prime }} \right)\) lân lượt là ảnh của \(A,\Delta ,(C)\) qua phép tịnh tiến theo \(\vec v = (1;2)\).
Gợi ý:
* Ta có: \({T_{\vec v}}(A) = {A^\prime }(2;3)\).
* Kỹ năng xác định ảnh của đường thẳng qua phép tịnh tiến:
Phương pháp 1: Chọn 2 điểm bất kì trên \(\Delta \), xác định ảnh tương ứng. Đường thẳng \({\Delta ^\prime }\) cần tìm là đường thẳng qua hai ảnh.
Chọn \(A(1;1),B( - 1;0) \in \Delta \)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{T_{\vec v}}(A) = {A^\prime }(2;3) \in {\Delta ^\prime }}\\{{T_{\vec v}}(B) = {B^\prime }(0;2) \in {\Delta ^\prime }}\end{array} \Rightarrow {\Delta ^\prime } \equiv {A^\prime }{B^\prime }.} \right.\)
Đường thẳng \({\Delta ^\prime }\) đi qua điểm \({A^\prime }(2;3)\) và có 1 vectơ chỉ phương \(\overrightarrow {{A^\prime }{B^\prime }} = ( - 2; - 1) \Rightarrow \vec n = ( - 1;2)\) là 1 vectơ pháp tuyến của \({\Delta ^\prime }\) nên \({\Delta ^\prime }: - 1(x - 2) + 2(y - 3) = 0 \Leftrightarrow - x + 2y - 4 = 0\).
Lưu ý: Hoàn toàn các em có thể để phưong trình ở dạng tham số, nhưng các câu hỏi trắc nghiệm thì thường sủ dụng kết quả là phưong trình tồng quát!
Phương pháp 2: Theo tính chât của phép tịnh tiến: Biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
Gọi \({\Delta ^\prime }\) là ảnh của đường thẳng \(\Delta \). Suy ra: \({\Delta ^\prime }:x - 2y + m = 0\).
Chọn \(A(1;1) \in \Delta \Rightarrow {T_{\bar v}}(A) = {A^\prime }(2;3) \in {\Delta ^\prime }\).
Ta có: \(2 - 6 + m = 0 \Leftrightarrow m = 4\). Vậy \({\Delta ^\prime }:x - 2y + 4 = 0\).
Phương pháp 3: Sủ dụng quỹ tích: \(\quad \forall M \in \Delta \Rightarrow {T_{\bar v}}(M) = {M^\prime } \in {\Delta ^\prime }\)
Gọi \(M(x;y) \in \Delta \Rightarrow {T_{\bar v}}(M) = {M^\prime }\left( {{x^\prime };{y^\prime }} \right):\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x + 1}\\{{y^\prime } = y + 2}\end{array}} \right.\)
\(\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = {x^\prime } - 1}\\{y = {y^\prime } - 2}\end{array}} \right.\)
Lúc đó: \(M\left( {{x^\prime } - 1;{y^\prime } - 2} \right) \in \Delta \)
\( \Leftrightarrow \left( {{x^\prime } - 1} \right) - 2\left( {{y^\prime } - 2} \right) + 1 = 0 \Leftrightarrow {x^\prime } - 2{y^\prime } + 4 = 0\).
Vậy \({\Delta ^\prime }:x - 2y + 4 = 0\).
Nhân xét: Trong 3 phưong pháp trên,
+) Phương pháp 1 tỏ ra hiệu quả cho tất cả các phép biến hình (dù dài dòng).
+) Phương pháp 2 tốt vì sử dụng tính chất phép tịnh tiến.
+) Phương pháp 3 nhanh hơn, phù hợp với trắc nghiệm và việc xác định ảnh của các hình Elíp, parabol....
* Xác định ảnh của đường tròn:
Phương pháp 1: Theo tính chất của phép tịnh tiến: Biến đường tròn thành đường tròn có cùng bán kính.
Ta có \((C) \equiv (I;R):\left\{ {\begin{array}{*{20}{l}}{I(1; - 2)}\\{R = \sqrt 6 }\end{array}} \right.\)
Ta có: \({T_{\vec v}}(I) = {I^\prime }(2;0)\) là tâm của đường tròn ảnh \(\left( {{C^\prime }} \right)\).
Vậy đường tròn \(\left( {{C^\prime }} \right)\) có tâm \({I^\prime }(2;0)\) và bán kính \({R^\prime } = R = \sqrt 6 :{(x - 2)^2} + {y^2} = 6\).
Phương pháp 2: Sủ dụng quĩ tích.
Gọi \(M(x;y) \in (C) \Rightarrow {T_{\bar v}}(M) = {M^\prime }\left( {{x^\prime };{y^\prime }} \right):\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x + 1}\\{{y^\prime } = y + 2}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = {x^\prime } - 1}\\{y = {y^\prime } - 2}\end{array}} \right.\)
Lúc đó: \(M\left( {{x^\prime } - 1;{y^\prime } - 2} \right) \in (C)\)
\( \Leftrightarrow {\left( {{x^\prime } - 1} \right)^2} + {\left( {{y^\prime } - 2} \right)^2} - 2\left( {{x^\prime } - 1} \right) + 4\left( {{y^\prime } - 2} \right) - 1 = 0\)
\( \Leftrightarrow {\left( {{x^\prime }} \right)^2} + {\left( {{y^\prime }} \right)^2} - 4{x^\prime } - 2 = 0\).
Vậy \(\left( {{C^\prime }} \right):{x^2} + {y^2} - 4x - 2 = 0\).
Bài tập 2: Cho hai đường thẳng \(d:3x - y - 3 = 0,\Delta :x + y = 0\). Phép tịnh tiến theo \(\vec v\) biến d thành \({d^\prime }:3x - y + 1 = 0,\Delta \) thành \({\Delta ^\prime }:x + y - 6 = 0\). Tìm tọa độ của \(\vec v\).
Gợi ý: Gọi \(\vec v = (a;b)\).
Chọn \(A(1;0) \in d \Rightarrow {T_{\vec v}}(A) = {A^\prime }(1 + a;b) \in {d^\prime }\).
\( \Leftrightarrow 3(1 + a) - 3b + 1 = 0 \Leftrightarrow 3a - 3b = - 4{\rm{ (1) }}\)
Chọn B \((1; - 1) \in \Delta \Rightarrow {T_{\vec v}}(B) = {A^\prime }(1 + a; - 1 + b) \in {\Delta ^\prime }\)
\( \Leftrightarrow (1 + a) + ( - 1 + b) - 6 = 0 \Leftrightarrow a + b = 6(2)\)
Từ (1) và (2) giải được: \(a = \frac{7}{3},b = 3\). Vậy \(\vec v = \left( {\frac{7}{3};3} \right)\).
Bài tập 1. Cho đường thẳng \(\Delta :6x + 2y - 1 = 0\). Tìm các vectơ \(\vec v \ne \vec 0\) sao cho: \({T_{\vec v}}(\Delta ) = \Delta \).
Gợi ý: \(\vec v = k( - 1;3);(k \ne 0)\).
Nhân xét: Có 2 trường hợp qua phép tịnh tiến, đường thẳng \(\Delta \) có ảnh là chính nó.
Truờng hơp 1: \({T_{\vec v}}\) với \(\vec v = \vec 0\).
Trường hơp 2: \({T_{\vec v}}\) với \(\vec v\) là 1 vectơ chỉ phương của \(\Delta \).
Bài tâp 2: Cho 2 điểm \(A( - 5;2),C( - 1;0)\). Biết: \(B = {T_{iu}}(A),C = {T_{\hat v}}(B)\). Tìm \(\vec u,\vec v\) đề có thế thực hiện phép tịnh tiến biến A thành C ?
Gợi ý:
Cách 1: Gọi \(\vec u = \left( {{u_1};{u_2}} \right),\vec v = \left( {{v_1};{v_2}} \right)\) thỏa yêu câu bài toán.
Ta có: \({T_{\vec u}}(A) = B \Leftrightarrow B\left( { - 5 + {u_1};2 + {u_2}} \right)\).
Và \({T_{\vec v}}(B) = C \Leftrightarrow C\left( { - 5 + {u_1} + {v_1};2 + {u_2} + {v_2}} \right) = ( - 1;0)\).
Vậy ta có: \(\left\{ {\begin{array}{*{20}{l}}{ - 5 + {u_1} + {v_1} = - 1}\\{2 + {u_2} + {v_2} = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{u_1} + {v_1} = 4}\\{{u_2} + {v_2} = - 2}\end{array}} \right.} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{v_1} = 4 - {u_1}}\\{{v_2} = - 2 - {u_2}}\end{array}} \right.\)
Kết luận 2 vectơ cân tìm có dạng:
\(\vec u = \left( {{u_1};{u_2}} \right),\vec v = \left( {4 - {u_1}; - 2 - {u_2}} \right)\quad \left( {{u_1};{u_2} \in \mathbb{R}} \right)\)
Cách 2: Ta có: \[\left\{ {\begin{array}{*{20}{l}}{{T_{\vec u}}(A) = B}\\{{T_{\vec v}}(B) = C}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\overrightarrow {AB} = \vec u}\\{\overrightarrow {BC} = \vec v}\end{array}} \right.} \right.\]
\[\begin{array}{l} \Leftrightarrow \overrightarrow {AB} + \overrightarrow {BC} = \vec u + \vec v\\ \Leftrightarrow \vec u + \vec v = \overrightarrow {AC} = (4; - 2)\left( {^*} \right)\end{array}\]
Gọi \(\vec u = \left( {{u_1};{u_2}} \right)\). Từ đẳng thức (*) suy ra được: \(\vec v = \left( {4 - {u_1}; - 2 - {u_2}} \right)\) (y.c.b.t)
Nhân xét: Cách 2 tỏ ra tốt hơn, có tính tư duy cao hơn.
Dạng toán: Sử dụng phép biến hình để tìm quỹ tích
Để giải tốt bài toán quỹ tích, ta cần nắm rõ một số nhận xét sau:
* Xác định các yếu tố cố định (không thay đổi), và điểm di động ban đầu.
* Biểu diễn điểm (cần tìm quỹ tích) theo điểm đi động ban đầu thông qua các yếu tố cố định. Cụ thể: Chẳng hạn, đối với phép tịnh tiến, biểu diễn: \(\overrightarrow {M{M^\prime }} = \vec v\). Suy ra: Tôn tại \({T_{\vec v}}(M) = {M^\prime }\), do \(M \in (H)\) nên \({M^\prime } \in \left( {{H^\prime }} \right)\), với \(\left( {{H^\prime }} \right)\) là ảnh của hình \((H)\) qua \({T_{\vec v}}\). Vậy quý tích cân tìm của điểm \({M^\prime }\) là \(\left( {{H^\prime }} \right).\)
Bài tâp 3: Trên đường tròn (C) cho hai điểm A, B cố định và điểm M thay đổi. Tìm quỹ tích điểm \({M^\prime }\) sao cho \(\overrightarrow {M{M^\prime }} + \overrightarrow {MA} = \overrightarrow {MB} \).
Gợi ý:
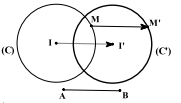
Ta có: \(\overrightarrow {M{M^\prime }} + \overrightarrow {MA} = \overrightarrow {MB} \Leftrightarrow \overrightarrow {{M^\prime }} = \overrightarrow {MB} - \overrightarrow {MA} \Leftrightarrow \overrightarrow {{M^\prime }} = \overrightarrow {AB} \).
Suy ra: \({T_{\overline {AB} }}(M) = {M^\prime }\).
Do \(M \in (C) \Rightarrow {M^\prime } \in \left( {{C^\prime }} \right)\) với \(\left( {{C^\prime }} \right)\) là ảnh của (C) qua \({T_{\overline {AB} }}\).
Tương tụ:
1) \(\overrightarrow {A{M^\prime }} = \frac{{\overrightarrow {MB} - 3\overrightarrow {MA} }}{2}\).
2) \(\overrightarrow {{M^\prime }M} - \overrightarrow {{M^\prime }A} + 2\overrightarrow {{M^\prime }B} = \vec 0\).
Bài tập 4: Cho hình bình hành ABCD, hai đỉnh A, B cố định, tâm I của hình bình hành thay đồi di động trên đường tròn (C). Tìm quỹ tích trung điểm M của cạnh BC.
Gợi ý:
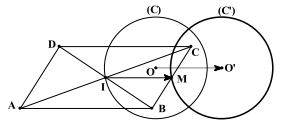
Dễ thấy: \(\overrightarrow {IM} = \frac{1}{2}\overrightarrow {AB} \), suy ra: \({T_{\frac{1}{2}}}\overrightarrow {AB} (I) = M\)
Do \(I \in (C) \Rightarrow {I^\prime } \in \left( {{C^\prime }} \right)\) với \(\left( {{C^\prime }} \right)\) là ảnh của \((C)\) qua \({T_{\frac{1}{2}\overrightarrow {AB} }}\).
Bài tâp 4: Trong mặt phẳng cho 2 đường thăng d và \({d_1}\) cắt nhau, hai điểm A, B cố định không thuộc hai đường thẳng đó sao cho AB không song song và không trùng với d và \({d_1}\). Tìm \(M \in d\) và \({M^\prime } \in {d_1}\) sao cho \(ABM{M^\prime }\) là hình bình hành.
Gợi ý:
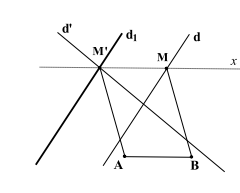
* Phân tích: Do \(ABM{M^\prime }\) là hình bình hành nên: \(\overrightarrow {M{M^\prime }} = \overrightarrow {BA} \).
Suy ra: \({T_{\overline {BA} }}(M) = {M^\prime }\).
Do \(M \in d\) nên \({M^\prime } \in {d_1}\) nên suy ra: \({M^\prime } \in {d^\prime } \cap {d_1}\).
* Cách dựng:
Bước 1: Dựng đường thẳng \({d_1}\) là ảnh của d qua \({T_{\overrightarrow {BA} }}\).
Bước 2: Xác định \({M^\prime } \in {d^\prime } \cap {d_1}\).
Bước 3: Dựng đường thẳng \(Mx//AB\) cắt d tại M.
* Số nghiệm bài toán: Điểm \(M \in d\) và \({M^\prime } \in {d_1}\) xác định là duy nhất, vì \({d^\prime } \cap {d_1}\) và \(Mx//AB\) cắt d lần lượt tại \({M^\prime },M\) duy nhất.
Bài toán cơ bản 1: Cho đường thẳng d và hai điểm A, B nằm khác phía với đường thẳng d. Xác định điểm M trên d sao cho MA + MB đạt giá trị nhỏ nhất.
Phương pháp:
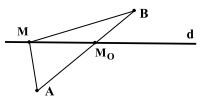
Dễ thấy \(MA + MB \ge AB\)
\( \Rightarrow (MA + MB){\rm{ Min }} \Leftrightarrow MA + MB = AB\)
Vậy điểm \(M \equiv {M_0} = AB \cap d\).
Bài toán cơ bản 2: Cho đường thẳng d và hai điểm A, B nằm cùng phía với đường thẳng d. Xác định điểm M trên d sao cho MA + MB đạt giá trị nhỏ nhất.
Phương pháp: Đưa bài toán về bài dạng 1 .
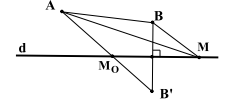
Lấy đối xứng điểm B qua đường thẳng d là điểm \({{\rm{B}}^\prime }\).
Lúc đó: \(MA + MB = MA + M{B^\prime } \ge A{B^\prime }\)
\( \Rightarrow (MA + MB){\mathop{\rm Min}\nolimits} \Leftrightarrow (MA + MB){\mathop{\rm Min}\nolimits} = A{B^\prime }\)
Vậy điểm \(M \equiv {M_0} = A{B^\prime } \cap d\)
Bài tâp 5: Cho 2 đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song và hai điểm A, B như hình vẽ. Tìm M \(M \in {\Delta _1}\) và \(N \in {\Delta _2}\) sao cho: AM + MN + NB nhỏ nhất .
Gợi ý:
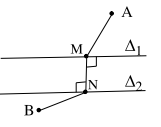
Nhận xét: Đưa bài toán vê các bài toán cơ bản (áp dụng với 1 đường thẳng) Thực hiện phép tịnh tiến \({T_{\overline {NM} }}\) (Do M N không đổi)
Ta có: \({T_{\overline {NM} }}(B) = B'\)
Lúc đó: AM + MN + NB = AM + MN MB’
Đế ý rằng: Do $M N$ không đổi, nên \((AM + MN + NB)\) nhỏ nhất \( \Leftrightarrow \left( {AM + M{B^\prime }} \right)\) nhỏ nhất
Ta thấy: \(AM + M{B^\prime } \ge A{B^\prime }\) nên \(\left( {AM + M{B^\prime }} \right)\) nhỏ nhất
\( \Leftrightarrow M \equiv {M_O} = A{B^\prime } \cap {\Delta _1}\).
* Cách dựng:
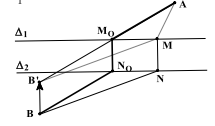
Bước 1: Thực hiện\(\underline {{\rm{ }}{T_{\overline {{\rm{NM}}} }}} (B) = {B^\prime }\).
Bước 2: Nối\(\underline {{\rm{ }}A{B^\prime }} \) cắt \({\Delta _1}\) tại \({M_0}\).
Dựng đường thẳng vuông góc với \({\Delta _1}\) cắt \({\Delta _2}\) tại \({N_0}\) cần tìm.