Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết và bài tập Nguyên hàm tích phân Toán lớp 12, tài liệu bao gồm 55 trang, tuyển chọn Lý thuyết và bài tập Nguyên hàm tích phân Toán lớp 12 đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

A. LÝ THUYẾT NGUYÊN HÀM - TÍCH PHÂN

I. NGUYÊN HÀM

1. Nguyên hàm là gì?

Định nghĩa: Cho hàm số f(x) xác định trên K ( K là khoảng, đoạn hay nưa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu \({F^\prime }(x) = f(x)\) với mọi \(x \in K\).

Định lí:

1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x)=F(x)+C cũng là một nguyên hàm của f(x) trên K.

2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x)+C, với C là một hằng số.

Do đó \(F(x) + C,C \in \mathbb{R}\) là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu \(\int f (x)dx = F(x) + C\).

2. Tính chất của nguyên hàm

Tỉnh chất 1: \({\left( {\int f (x)dx} \right)^\prime } = f(x)\) và \(\int {{f^\prime }} (x)dx = f(x) + C\)

Tính chất 2: \(\int k f(x)dx = k\int f (x)dx\) với k là hằng số khác 0 .

Tinh chất 3: \(\int {\left[ {f(x) \pm g(x)} \right]d{\rm{x}} = \int {f(x)d{\rm{x}} \pm \int {g(x)d{\rm{x}}} } } \)

3. Sự tồn tại của nguyên hàm

Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

4. Bảng nguyên hàm của một số hàm số sơ cấp

II. TÍCH PHÂN

1. Định nghĩa

Cho hàm số $f(x)$ liên tục trên đoạn $[a;b]$. Giả sử $F(x)$ là một nguyên hàm của hàm số $f(x)$ trên đoạn $[a;b]$, hiệu số $F(b)-F(a)$ được gọi là tích phân từ $a$ đến $b$ (hay tích phân xác định trên đoạn $[a;b]$ của hàm số $f(x)$.

Kí hiệu là : ${\int }_a^{b}f(x)dx$

Vậy ta có :${\int }_a^{b}f(x)dx=F(b)-F(a)=F(x){|}_a^b$

Chú ý : Trong trường hợp a = b, ta định nghĩa: ${\int }_a^{a}f(x)dx=0$

Trường hợp a>b, ta định nghĩa: ${\int }_a^{b}f(x)dx=-{\int }_b^{a}f(x)dx$

Tích phân không phụ thuộc vào chữ dùng làm biến số trong dấu tích phân, tức là :

${\int }_a^{b}f(x)dx={\int }_a^{b}f(t)dt={\int }_a^{b}f(u)du=...$ (vì đều bằng $F(b)-F(a)$)

2. Tính chất của tích phân

${\int }_a^{b}kf(x)dx=k{\int }_a^{b}f(x)dx$  ( với $k$ là hằng số)

${\int }_a^b\left[f\left(x\right)\pm g\left(x\right)\right]d\mathrm{x}={\int }_a^{b}f\left(x\right)d\mathrm{x}\pm {\int }_a^{b}g\left(x\right)d\mathrm{x}$

${\int }_a^{b}f(x)dx={\int }_a^{c}f(x))dx+{\int }_c^{b}f(x)dx$ (với $a<b<c$)

Đặc biệt:

Nếu hàm y = f(x) là hàm số lẻ trên $\left[-a;a\right]$ thì ${\int }_{-a}^{a}f\left(x\right)dx=0$

Nếu hàm y = f(x) là hàm số chẵn trên  $\left[-a;a\right]$ thì ${\int }_{-a}^{a}f\left(x\right)dx=2{\int }_0^{a}f\left(x\right)dx$

III. PHƯƠNG PHÁP GIẢI NGUYÊN HÀM - TÍCH PHÂN

1. Phương pháp đổi biến số

Định lí 1: Nếu $\int f(u)du=F(u)+C$ và u=u(x) là hàm số có đạo hàm liên tục thì

$\int f(u(x))u^{\mathrm{\prime }}(x)dx=F(u(x))+C$

Hệ quả: Nếu $u=ax+b(a\ne 0)$ thì ta có $\int f(ax+b)dx=\frac{1}{a}F(ax+b)+C$

2. Phương pháp từng phần

Định lí 2: Nếu hai hàm số u=u(x) và v=v(x) có đạo hàm liên tục trên K thì

$\int u(x)v^{\mathrm{\prime }}(x)dx=u(x)v(x)-\int u^{\mathrm{\prime }}(x)v(x)dx$

Hay $\int udv=uv-\int vdu$

*Lưu ý: phương pháp giải tích phân tương tự phương pháp giải nguyên hàm, chỉ khác ở việc thêm cận cho tích phân

B. BÀI TẬP NGUYÊN HÀM - TÍCH PHÂN

Câu 1. Nguyên hàm của hàm số$f(x)=x^3+3x+2$ là hàm số nào trong các hàm số sau?

A. $F(x)=\frac{x^4}{4}+\frac{3x^2}{2}+2x+C$.

B. $F(x)=\frac{x^4}{3}+3x^2+2x+C$.

C. $F(x)=\frac{x^4}{4}+\frac{x^2}{2}+2x+C$.

D. $F(x)=3x^2+3x+C$.

Câu 2. Hàm số $F(x)=5x^3+4x^2-7x+120+C$ là họ nguyên hàm của hàm số nào sau đây?

A. $f(x)=15x^2+8x-7$.

B. $f(x)=5x^2+4x+7$.

C. $f(x)=\frac{5x^2}{4}+\frac{4x^3}{3}-\frac{7x^2}{2}$.

D. $f(x)=5x^2+4x-7$.

Câu 3. Tìm nguyên hàm của hàm số $f(x)={\sin }^{3}x\cdot \cos x$.

A. $\int f(x)dx=\frac{{\sin }^{4}x}{4}+C$.

B. $\int f(x)dx=-\frac{{\sin }^{4}x}{4}+C$.

C. $\int f(x)dx=\frac{{\sin }^{2}x}{2}+C$.

D. $\int f(x)dx=-\frac{{\sin }^{2}x}{2}+C$.

Câu 4. Họ nguyên hàm của hàm số $f(x)=e^x(3+e^{-x})$là

A. $F(x)=3e^x+x+C$.

B. $F(x)=3e^x+e^x\ln e^x+C$.

C. $F(x)=3e^x-\frac{1}{e^x}+C$.

D. $F(x)=3e^x-x+C$.

Câu 5. Tìm nguyên hàm của hàm số $f(x)=\frac{1}{\sqrt{3-x}}$.

A. $\int f(x)dx=-2\sqrt{3-x}+C$.

B. $\int f(x)dx=-\sqrt{3-x}+C$.

C. $\int f(x)dx=2\sqrt{3-x}+C$.

D. $\int f(x)dx=-3\sqrt{3-x}+C$.

Câu 6. Tìm nguyên hàm của hàm số $f(x)=\sqrt{2x+1}$.

A. $\int f(x)dx=\frac{1}{3}(2x+1)\sqrt{2x+1}+C$.

B. $\int f(x)dx=\frac{2}{3}(2x+1)\sqrt{2x+1}+C$.

C. $\int f(x)dx=-\frac{1}{3}\sqrt{2x+1}+C$.

D. $\int f(x)dx=\frac{1}{2}\sqrt{2x+1}+C$.

Câu 7. Tính 

A. 4.    

B. 4ln2.    

C. 4/ln⁡2.    

D. 6.

Câu 8. Cho 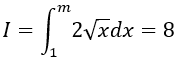. Tìm m?

Câu 9. Tính 

A. 0.    

B. 9.    

C. 18.    

D. -9.

Câu 10. Tính 

Câu 11: Tính 

A. 2e² - 2e + 4.

B. 2e³ + 2e + 2.

C. 2e² - 2e + 8.

D. 2e² + 2e + 8.

Câu 12: Cho

với a; b;c là các số nguyên. Mệnh đề nào dưới đây đúng?

A. a + b + c = 0.

B. a - 2b + c = 0.

C. a - b + c = -1.

D. a + 2b = 0.