Có bao nhiêu cặp số nguyên (x,y) thỏa mãn

${\log }_3\left(x^2+y^2+x\right)+{\log }_2\left(x^2+y^2\right)\le {\log }_{3}x+{\log }_2\left(x^2+y^2+24x\right)?$

Chọn B

Điều kiện: x>0.

Ta có: ${\log }_3\left(x^2+y^2+x\right)+{\log }_2\left(x^2+y^2\right)\le {\log }_{3}x+{\log }_2\left(x^2+y^2+24x\right)$

$\iff {\log }_3\left(x^2+y^2+x\right)-{\log }_{3}x\le {\log }_2\left(x^2+y^2+24x\right)-{\log }_2\left(x^2+y^2\right)$

$\iff {\log }_3\left(\frac{x^2+y^2+x}{x}\right)\le {\log }_2\left(\frac{x^2+y^2+24x}{x^2+y^2}\right)$$\iff {\log }_3\left(1+\frac{x^2+y^2}{x}\right)\le {\log }_2\left(1+\frac{24x}{x^2+y^2}\right)$

$\iff {\log }_3\left(\frac{x^2+y^2}{x}+1\right)-{\log }_2\left(1+\frac{24x}{x^2+y^2}\right)\le 0.$

Đặt: $t=\frac{x^2+y^2}{x}(t>0)$, bất phương trình trở thành: ${\log }_3(1+t)-{\log }_2\left(1+\frac{24}{t}\right)\le 0$ (1).

Xét hàm số $f\left(t\right)={\log }_3(1+t)-{\log }_2\left(1+\frac{24}{t}\right)$ có $f^{\text{'}}\left(t\right)=\frac{1}{(1+t)\ln 3}+\frac{24}{\left(t^2+24t\right)\ln 2}>0,\forall t>0$.

Suy ra hàm số đồng biến trên khoảng $(0;+\infty )$.

Ta có $f\left(8\right)={\log }_3(1+8)-{\log }_2\left(1+\frac{24}{8}\right)=0$

Từ đó suy ra: $\left(1\right)\iff f\left(t\right)\le f\left(8\right)\iff t\le 8\iff \frac{x^2+y^2}{x}\le 8\iff {(x-4)}^2+y^2\le 16$.

Đếm các cặp giá trị nguyên của $(x;y)$

Ta có: ${(x-4)}^2\le 16\iff 0\le x\le 8$, mà x>0 nên $0<x\le 8$.

Với $x=1,x=7\Rightarrow y=\{\pm 2;\pm 1;0\}$ nên có 10 cặp.

Với $x=2,x=6\Rightarrow y=\{\pm 3;\pm 2;\pm 1;0\}$ nên có 14 cặp.

Với $x=3,x=5\Rightarrow y=\{\pm 3;\pm 2;\pm 1;0\}$ nên có 14 cặp.

Với $x=4\Rightarrow y=\{\pm 4;\pm 3;\pm 2;\pm 1;0\}$ nên có 9 cặp.

Với $x=8\Rightarrow y=0$ có 1 cặp.

Vậy có 48 cặp giá trị nguyên $(x;y)$ thỏa mãn đề bài.

Các dạng bài tập giải bất phương trình logarit

Dạng 1. Bất phương trình logarit cơ bản

Ta có BPT log_ax ≥ m (log_ax ≤ m; log_ax < m; log_ax > m) 

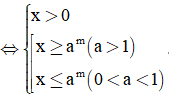
Dạng 2. Phương pháp đưa về cùng cơ số

Xét bất phương trình log_af(x) > log_ag(x) (a > 0, a ≠ 1)  

• Nếu a > 1 thì log_af(x) > log_ag(x) ⇔ f(x) > g(x) (cùng chiều khi a > 1)

• Nếu 0 < a < 1 thì log_af(x) > log_ag(x) ⇔ f(x) < g(x) (ngược chiều khi 0 < a < 1 )

• Nếu a chứa ẩn thì log_af(x) > log_ag(x) ⇔ 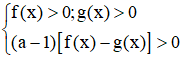 (hoặc chia 2 trường hợp của cơ số)

Dạng 3. Phương pháp đặt ẩn phụ

Tương tự với phương pháp giải phương trình logarit bằng phương pháp đặt ẩn phụ nhưng lưu ý tới chiều biến thiên của hàm số. 

Dạng 4. Phương pháp mũ hóa

Tương tự với giải phương trình logarit bằng phương pháp mũ hóa.

Dạng 5. Phương pháp hàm số, đánh giá

Cho hàm số y = f(x) xác định và liên tục trên D:

Nếu hàm số f(t) luôn đồng biến trên D và ∀u,v ∈ D thì f(u) > f(v) ⇔ u > v

Nếu hàm số f(t) luôn nghịch biến trên D và ∀u,v ∈ D thì f(u) > f(v) ⇔ u < v

Bài tập liên quan:

Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 0 ≤ x ≤ 2020 và log2(4x + 4) + x = y + 1 + 2y?

Cách giải:

log₂(4x + 4) +x = y + 1 + 2^y

⇔ log₂[4(x + 1)] + x = y + 1 + 2^y

⇔ log₂4 + log₂(x + 1) + x = y + 1 + 2^y

⇔ log₂(x + 1) + 2 + x  = 2^y + y + 1 (*)

Xét f(a) = 2^a + a + 1

f'(a) = 2^a. ln2 + 1 > 0

Suy ra f(a) là hàm số đồng biến trên R

Phương trình (*) tương đương với:

f(log₂(x+1)) = f(y)

⇒ log₂(x + 1) = y

⇔ x + 1 = 2^y

⇔ x = 2^y – 1

Do 0 ≤ x ≤ 2020 suy ra: 0 ≤ 2^y – 1 ≤ 2020

⇔ 1 ≤ 2^y  ≤ 2021

⇔ 0 ≤ y ≤ 10,98

Vậy y ∈ {0;1;2;3;4;5;6;7;8;9;10} (có 11 số nguyên y)

Tương ứng có 11 số nguyên x

Vậy có 11 cặp số nguyên (x; y) thỏa mãn.

Tham khảo thêm một số tài liệu liên quan:

Bộ 15 Đề thi Toán 12 Giữa kì 2

30 Đề Thi Thử THPT QG Môn Toán Lớp 12