Trên tập hợp số phức, xét phương trình $z^2-2\left(m+1\right)z+m^2=0$ (m là số thực). Có bao nhiêu giá trị của m để phương trình đó có hai nghiệm phân biệt $z_1,z_2$ thỏa mãn $\left|z_1\right|+\left|z_2\right|=2?$

Chọn C

Giải chi tiết:

Ta có: ${\Delta }^{\text{'}}=2m+2$

TH1: ${\Delta }^{\text{'}}<0\iff m<-1.$

Phương trình có hai nghiệm phức, khi đó: $\left|z_1\right|=\left|z_2\right|=\sqrt{\frac{c}{a}}=\sqrt{m^2}.$

Suy ra: $2\sqrt{m^2}=2\iff \left[\begin{array}{l}m=1\\ m=-1\left(l\right)\end{array}\right..$

TH2: ${\Delta }^{\text{'}}>0\iff m>-1.$

Vì $a.c=m^2\ge 0$ nên phương trình có hai nghiệm phân biệt $z_1.z_2\ge 0$

 hoặc $z_1.z_2\le 0.$

Suy ra: $\left|z_1\right|+\left|z_2\right|=2\iff \left|z_1+z_2\right|=2\iff \left|2m+2\right|=2\iff \left[\begin{array}{l}m=-2\left(l\right)\\ m=0\end{array}\right..$

Vậy có 2  giá trị của m thỏa yêu cầu bài toán.

Phương pháp giải:

Cho phương trình: ax² + bx + c = 0 (a ≠ 0)

1. Điều kiện để phương trình có hai nghiệm phân biệt sao cho x₁ = px₂ (với p là một số thực)

B1- Tìm điều kiện để phương trình có hai nghiệm phân biệt .

B2- Áp dụng định lý Vi - ét tìm:

B3- Kết hợp (1) và (3) giải hệ phương trình: 

B4- Thay x₁ và x₂ vào (2) ⇒ Tìm giá trị tham số.

2. Điều kiện để phương trình có hai nghiệm thỏa mãn điều kiện: |x₁ - x₂| = k(k ∈ R)

- Bình phương trình hai vế: (x₁ - x₂)² = k² ⇔ ... ⇔ (x₁ + x₂)² - 4x₁x₂ = k²

- Áp dụng định lý Vi-ét tính x₁ + x₂ và x₁x₂ thay vào biểu thức ⇒ kết luận.

3. So sánh nghiệm của phương trình bậc hai với một số bất kỳ:

B1: Tìm điều kiện để phương trình có nghiệm (∆ ≥ 0)

B2: Áp dụng Vi-ét tính x₁ + x₂ và x₁x₂  (*)

+/ Với bài toán: Tìm m để phương trình có hai nghiệm > α

Ta có: 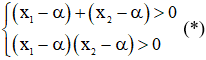. Thay biểu thức Vi-ét vào hệ(*) để tìm m

+/ Với bài toán: Tìm m để phương trình có hai nghiệm < α

Ta có: 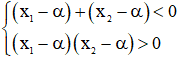  (*).Thay biểu thức Vi-ét vào hệ(*) để tìm m

+/ Với bài toán: Tìm m để phương trình có hai nghiệm: x₁ < α < x₂

Ta có: (x₁ - α)(x₂ - α) < 0 (*). Thay biểu thức Vi-ét vào (*) để tìm m

Bài tập liên quan:

Trên tập hợp số phức, xét phương trình ${𝑧}^2+2𝑚𝑧+1=0$ ( $𝑚$ là tham số thực). Có bao nhiêu giá trị nguyên của $𝑚$ để phương trình đã cho có hai nghiệm phân biệt ${𝑧}_1,{𝑧}_2$ thỏa mãn $|{𝑧}_1+3|=|{𝑧}_2+3|$ ?

Lời giải:

Xét phương trình $\left(1\right)$ : ${𝑧}^2+2𝑚𝑧+1=0$
Để phương trình $\left(1\right)$ có hai nghiệm phân biệt thì có 2 trường hợp:

TH1: Hai nghiệm ${𝑧}_1,{𝑧}_2\in \mathbb{𝑅}$ $$

$\Rightarrow {\mathrm{\Delta }}^{\prime }>0\iff {𝑚}^2-1>0\iff 𝑚<-1\vee 𝑚>1$

Khi đó: $$

$|{𝑧}_1+3|=|{𝑧}_2+3|\iff [\begin{array}{rl}& {𝑧}_1+3={𝑧}_2+3\\ & {𝑧}_1+3=-({𝑧}_2+3)\end{array}\iff [\begin{array}{rl}& {𝑧}_1={𝑧}_2\left(𝑙𝑜𝑎𝑖\right)\\ & {𝑧}_1+{𝑧}_2=-6\end{array}$

$$$$$\iff -2𝑚=-6\iff 𝑚=3$. So điều kiện, nhận $𝑚=3$.

TH2: Hai nghiệm ${𝑧}_1,{𝑧}_2\in \mathbb{𝐶}\mathrm{\setminus }\mathbb{𝑅}$ $\Rightarrow {\mathrm{\Delta }}^{\prime }<0\iff -1<𝑚<1$

Khi đó: $|{𝑧}_1+3|=|{𝑧}_2+3|\iff \sqrt{{(𝑎+3)}^2+{𝑏}^2}=\sqrt{{(𝑎+3)}^2+{(-𝑏)}^2}$ (luôn đúng).

Vì $𝑚$ nguyên nên nhận $𝑚=0$.

Vậy có 2 giá trị nguyên của $𝑚$ thoả đề.

Tham khảo thêm một số tài liệu liên quan:

Đề thi thử Toán sở GD&DT Thái Bình năm 2024

Đề thi thử Toán sở GD&DT Hải Phòng năm 2024