Cho hàm số bậc ba y=f(x) có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên của tham số m để phương trình f(x)=m có ba nghiệm thực phân biệt?

A. 2
B. 5
C. 3
D. 4
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số và đường thẳng .
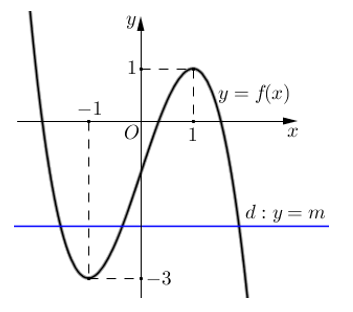
Dựa vào hình vẽ, ta có:
Phương trình có ba nghiệm thực phân biệt khi đường thẳng cắt đồ thị hàm số tại ba điểm phân biệt, tức là . Mà nên .
Phương pháp giải:
Cho hàm số y = f (x) có đồ thị (C1) và y = g (x) có đồ thị (C2) .
Phương trình hoành độ giao điểm của (C1) và (C2) là f (x) = g (x).
Khi đó: Số giao điểm của (C1) và (C2) bằng với số nghiệm của phương trình (1).
Trên tập hợp số phức, xét phương trình (m là số thực). Có bao nhiêu giá trị của m để phương trình đó có hai nghiệm phân biệt thỏa mãn
Có bao nhiêu giá trị nguyên của tham số m để hàm số có ba điểm cực trị?
Cho hàm số có đạo hàm liên tục trên R và thỏa mãn. Diện tích hình phẳng giới hạn bởi các đường và bằng
Cho hàm số f(x) liên tục trên R. Gọi là hai nguyên hàm của f(x) trên R thỏa mãn và . Khi đó bằng
Có bao nhiêu giá trị nguyên của tham số để hàm số đồng biến trên khoảng (0,1)?
Xét các số phức z thỏa mãn . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của . Giá trị của bằng
Cho hàm số có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là

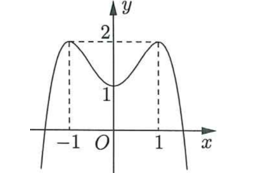
Cho hàm số có đồ thị là đường cong trong hình bên. Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
Trong không gian Oxyz cho Xét các điểm M thay đổi sao cho tam giácOAM không có góc tù và có diện tích bằng 15 Giá trị nhỏ nhất của độ dài đoạn thẳng MB thuộc khoảng nào dưới đây?
Trong không gian Oxyz, cho điểm và đường thẳng . Gọi (P) là mặt phẳng đi qua A và chứa d. Khoảng cách từ điểm đến (P) bằng