b) Tính khoảng biến thiên, khoảng tứ phân vị, phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm của Đà Lạt và Vũng Tàu.
 Giải bởi Vietjack
Giải bởi Vietjack
b)
Đà Lạt
Khoảng biến thiên của mẫu số liệu ghép nhóm của Đà Lạt là:
R = 91,5 – 78,3 = 13,2 (%).
Từ bảng thống kê trên, ta có bảng thống kê của mẫu số liệu ghép nhóm của Đà Lạt:
|
Nhóm |
Tần số |
Tần số tích lũy |
|
[78,3; 81,6) |
2 |
2 |
|
[81,6; 84,9) |
1 |
3 |
|
[84,9; 88,2) |
7 |
10 |
|
[88,2; 91,5) |
2 |
12 |
|
|
n = 12 |
|
Số phần tử của mẫu là n = 12.
- Ta có: mà 2 < 3. Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3. Xét nhóm 2 là nhóm [81,6; 84,9) có s = 81,6; h = 3,3; n2 = 1 và nhóm 1 là nhóm [78,3; 81,6) có cf1 = 2.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
(%).
- Ta có: mà 3 < 9 < 10. Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9. Xét nhóm 3 là nhóm [84,9; 88,2) có t = 84,9; l = 3,3; n3 = 7 và nhóm 2 là nhóm [81,6; 84,9) có cf2 = 3.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
(%).
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm của Đà Lạt là:
∆Q = Q3 – Q1 = 87,7 – 84,9 = 2,8 (%).
Số trung bình cộng của mẫu số liệu ghép nhóm của Đà Lạt là:
(%).
Vậy phương sai của của mẫu số liệu ghép nhóm của Đà Lạt là:
∙ [2 ∙ (79,95 – 85,725)2 + 1 ∙ (83,25 – 85,725)2 + 7 ∙ (86,55 – 85,725)2
+ 2 ∙ (89,85 – 85,725)2] = ≈ 9,3.
Độ lệch chuẩn của mẫu số liệu ghép nhóm của Đà Lạt là: (%).
Vũng Tàu
Khoảng biến thiên của mẫu số liệu ghép nhóm của Vũng Tàu là:
R' = 84,9 – 75 = 9,9 (%).
Từ bảng thống kê trên, ta có bảng thống kê của mẫu số liệu ghép nhóm của Vũng Tàu:
|
Nhóm |
Tần số |
Tần số tích lũy |
|
[75; 78,3) |
5 |
5 |
|
[78,3; 81,6) |
6 |
11 |
|
[81,6; 84,9) |
1 |
12 |
|
|
n = 12 |
|
Số phần tử của mẫu là n = 12.
- Ta có: mà 5 > 3. Suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3. Xét nhóm 1 là nhóm [75; 78,3) có s = 75; h = 3,3; n1 = 5.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
(%).
- Ta có: mà 5 < 9 < 11. Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9. Xét nhóm 2 là nhóm [78,3; 81,6) có t = 78,3; l = 3,3; n2 = 6 và nhóm 1 là nhóm [75; 78,3) có cf1 = 5.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
(%).
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm của Vũng Tàu là:
∆'Q = Q'3 – Q'1 = 80,5 – 76,98 = 3,52 (%).
Số trung bình cộng của mẫu số liệu ghép nhóm của Vũng Tàu là:
(%).
Vậy phương sai của của mẫu số liệu ghép nhóm của Vũng Tàu là:
∙ [5 ∙ (76,65 – 78,85)2 + 6 ∙ (79,95 – 78,85)2 + 1 ∙ (83,25 – 78,85)2]
= = 4,235.
Độ lệch chuẩn của mẫu số liệu ghép nhóm của Vũng Tàu là: (%).
Bảng 24 thống kê độ ẩm không khí trung bình các tháng năm 2021 tại Đà Lạt và Vũng Tàu (đơn vị: %).
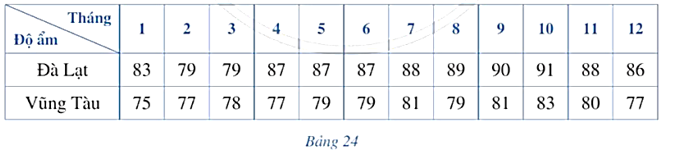
(Nguồn: Niên giám Thống kê 2021, NXB Thống kê, 2022)
a) Hãy lần lượt ghép các số liệu của Đà Lạt, Vũng Tàu thành năm nhóm sau:
[75; 78,3), [78,3; 81,6), [81,6; 84,9), [84,9; 88,2), [88,2; 91,5).
Bảng 22, Bảng 23 lần lượt biểu diễn mẫu số liệu ghép nhóm về nhiệt độ không khí trung bình các tháng năm 2021 tại Hà Nội và Huế (đơn vị: độ C).
|
Giá trị đại diện |
Tần số |
|
Nhóm |
Giá trị đại diện |
Tần số |
|
|
[16,8; 19,8) |
18,3 |
2 |
|
[16,8; 19,8) |
18,3 |
1 |
|
[19,8; 22,8) |
21,3 |
3 |
|
[19,8; 22,8) |
21,3 |
2 |
|
[22,8; 25,8) |
24,3 |
2 |
|
[22,8; 25,8) |
24,3 |
3 |
|
[25,8; 28,8) |
27,3 |
1 |
|
[25,8; 28,8) |
27,3 |
2 |
|
[28,8; 31,8) |
30,3 |
4 |
|
[28,8; 31,8) |
30,3 |
4 |
|
|
|
n = 12 |
|
|
|
n = 12 |
Bảng 22 Bảng 23
(Nguồn: Niên giám Thống kê 2021, NXB Thống kê, 2022)
a) Tính khoảng biến thiên, khoảng tứ phân vị, phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm của Hà Nội và Huế.
c) Trong hai thành phố Đà Lạt và Vũng Tàu, thành phố nào có độ ẩm không khí trung bình tháng đồng đều hơn?
Cho mẫu số liệu ghép nhóm có tứ phân vị thứ nhất, thứ hai, thứ ba lần lượt là Q1, Q2, Q3. Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó bằng:
A. 2Q2.
B. Q1 – Q3.
C. Q3 – Q1.
D. Q3 + Q1 – Q2.
b) Trong hai thành phố Hà Nội và Huế, thành phố nào có nhiệt độ không khí trung bình tháng đồng đều hơn?