A. 4;
B. 8;
C. 6;
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
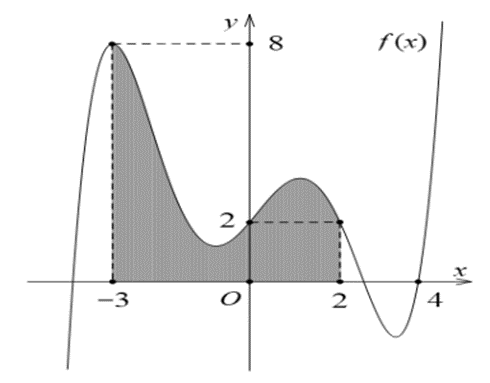
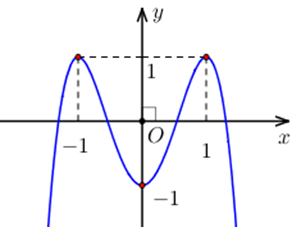
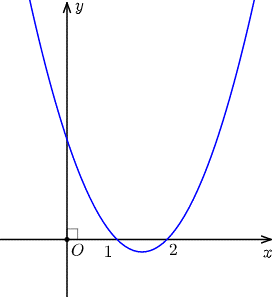
Dựa vào đồ thị hàm số ta thấy
f (f (x) - 1) = 0
+) TH1: f (x) - 1 = a Û f (x) = a + 1 (-1 < a + 1 < 0)
Phương trình cho ít nhất 4 nghiệm phân biệt
+) TH2: f (x) - 1 = b Û f (x) = b + 1 (0 < b + 1 < 1)
Phương trình cho 4 nghiệm phân biệt
+) TH3: f (x) - 1 = c Û f (x) = c + 1 (1 < c + 1 < 2)
Phương trình vô nghiệm
+) TH4: f (x) - 1 = d Û f (x) = d + 1 (2 < d + 1 < 3)
Phương trình vô nghiệm
Vậy suy ra phương tình f (f (x) - 1) = 0 cho ít nhất 8 nghiệm phân biệt.
Cho hàm số . Giả sử F là nguyên hàm của f trên ℝ thỏa mãn F(0) = 2. Giá trị của F (-1) + 2F (2) + 6 bằng?
Cho hai số phức z1 = 2 - i và z2 = 1 + 2i. Khi đó phần ảo của số phức z1.z2 bằng:
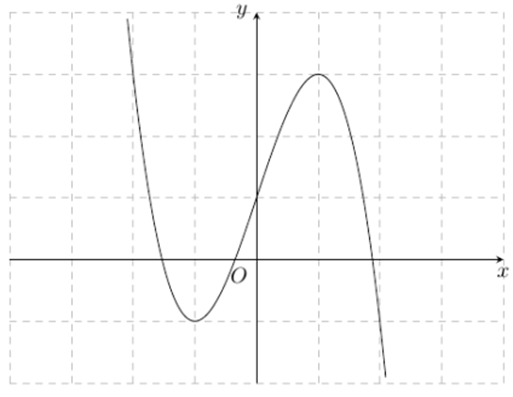
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
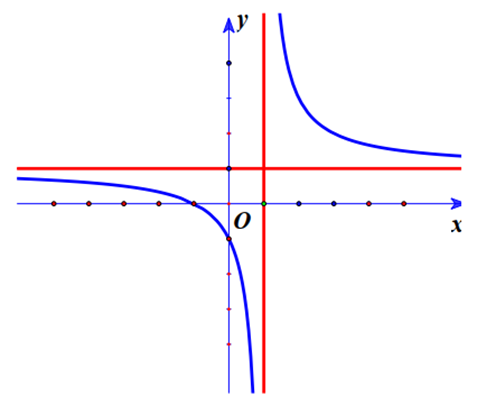
Biết hàm số (a là số thực cho trước, a -1) có đồ thị như trong hình bên. Mệnh đề nào dưới đây đúng?
Trong không gian Oxyz, cho điểm M(3; 1; 2). Tìm tọa độ điểm N là điểm đối xứng của M qua trục Ox
Cho số phức z thỏa mãn . Trong mặt phẳng tọa độ Oxy, tập hợp tất cả các điểm biểu diễn cho số phức z là đường thẳng nào trong các đường thẳng sau đây?
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và . Gọi D là đường thẳng song song với (P): x + y + z - 7 = 0 và cắt d1, d2 lần lượt tại A, B sao cho AB ngắn nhất. Phương trình đường thẳng D là
Cho số phức z thỏa mãn |z - 1 - 2i| = 3. Tính giá trị nhỏ nhất của biểu thức P = |z - 4 - 6i|.
Cho số phức z thỏa mãn . Điểm biểu diễn của số phức z có tọa độ là