Cho hai số phức z1 = 2 - i và z2 = 1 + 2i. Khi đó phần ảo của số phức z1.z2 bằng:...

Question

Cho hai số phức z1 = 2 - i và z2 = 1 + 2i. Khi đó phần ảo của số phức z1.z2 bằng:

VietJack · Accepted Answer

Đáp án đúng là: B Bài giải: Ta có z1.z2 = (2 - i)(1 + 2i) = 2 + 4i - i - 2i2 = 2 + 4i - i + 2 = 4 + 3i Khi đó phần ảo của số phức z1.z2 bằng 3. Phép tính với số phức: Cho hai số phức z1 = a + bi và z2 = c + di thì: • Phép cộng số phức: z1 + z2 = (a + c) + (b + d)i • Phép trừ số phức: z1 - z2 = (a - c) + (b - d)i - Mọi số phức z = a + bi thì số đối của z là -z = -a - bi: z + (-z) = (-z) + z = 0 • Phép nhân số phức: z1.z2 = (ac - bd) + (ad + bc)i • Phép chia số phức: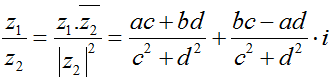 (với z2 ≠ 0) - Chú ý : • Với mọi số thực k và mọi số phức z = a + bi thì: k(a + b)i = ka + kbi • Với mọi số phức: 0z = 0 • Phép cộng và phép nhân các số phức có tất cả các tính chất của phép cộng và phép nhân của số thực. • i4k = 1; i4k + 1 = i; i4k + 2 = -1; i4k + 3 = -i Bài tập liên quan: Cho hai số phức z1=2+i và iz2=1+3i. Phần thực của số phức z1+z2 bằng A. 1 B. 3 C. 4 D. -2 Bài giải: Tham khảo thêm một số tài liệu liên quan: Trắc nghiệm Ôn thi THPT QG Toán 12: Đáp án hình học không gian mức độ vận dụng Kiến thức nền Máy Tính Cầm Tay Casio có đáp án, chọc lọc

Nhóm	Giá trị đại diện	Tần số	Nhóm	Giá trị đại diện	Tần số
[16,8; 19,8)	18,3	2	[16,8; 19,8)	18,3	1
[19,8; 22,8)	21,3	3	[19,8; 22,8)	21,3	2
[22,8; 25,8)	24,3	2	[22,8; 25,8)	24,3	3
[25,8; 28,8)	27,3	1	[25,8; 28,8)	27,3	2
[28,8; 31,8)	30,3	4	[28,8; 31,8)	30,3	4
		n = 12			n = 12

Câu hỏi:

Cho hai số phức z₁ = 2 - i và z₂ = 1 + 2i. Khi đó phần ảo của số phức z₁.z₂ bằng:

A. -2i;

B. 3;

C. -2;

D. 3i.

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho hàm số $f (x) = \{\begin{matrix} 2 x + 5 k h i x \geq 1 \\ 3 x^{2} + 4 k h i x < 1 \end{matrix}$ . Giả sử F là nguyên hàm của f trên ℝ thỏa mãn F(0) = 2. Giá trị của F (-1) + 2F (2) + 6 bằng?

Câu 2:

Cho hàm số y = ax³ + bx² + cx + d có đồ thị như hình vẽ sau

Câu 3:

Trong không gian Oxyz, cho hai vectơ $\vec{u} = (1; 3; - 2)$ và $\vec{v} = (2; 1; - 1)$ . Tọa độ của vectơ $\vec{u} - \vec{v}$ là

Câu 4:

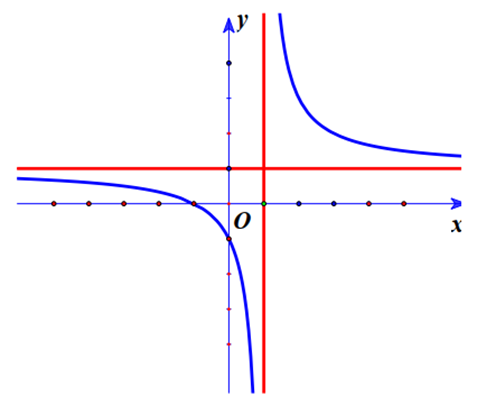
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?

Câu 5:

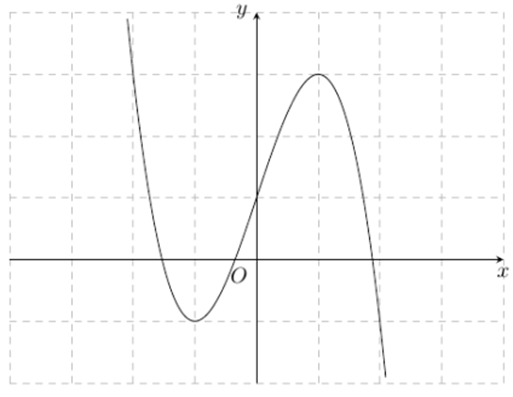
Biết hàm số $y = \frac{x + a}{x - 1}$ (a là số thực cho trước, a $\neq$ -1) có đồ thị như trong hình bên. Mệnh đề nào dưới đây đúng?

Câu 6:

Trên đoạn [1; 5], hàm số $y = x + \frac{4}{x}$ đạt giá trị nhỏ nhất tại điểm

Câu 7:

Trong không gian Oxyz, cho điểm M(3; 1; 2). Tìm tọa độ điểm N là điểm đối xứng của M qua trục Ox

Câu 8:

Cho hàm số y = f (x) có đồ thị y = f '(x) như hình sau. Hàm số y = f(3 - 2x) + 2022 đồng biến trên khoảng nào.

Câu 9:

Cho số phức z thỏa mãn $z = \bar{z}$ . Trong mặt phẳng tọa độ Oxy, tập hợp tất cả các điểm biểu diễn cho số phức z là đường thẳng nào trong các đường thẳng sau đây?

Câu 10:

Câu 11:

Cho số phức z thỏa mãn |z - 1 - 2i| = 3. Tính giá trị nhỏ nhất của biểu thức P = |z - 4 - 6i|.

Câu 12:

Cho số phức z thỏa mãn $i . \bar{z} = 5 + 2 i$ . Điểm biểu diễn của số phức z có tọa độ là

Câu 13:

Cho hàm số bậc bốn y = f (x) có đồ thị là đường cong trong hình bên. Phương trình f (f (x) - 1) = 0 có ít nhất bao nhiêu nghiệm?

Câu 14:

Cho hàm số y = f (x) liên tục trên có đồ thị như hình vẽ. Giả sử phần gạch dọc có diện tích bằng a. Tính theo a giá trị của tích phân $\int_{- 3}^{2} [1 + (2 x + 1) f^{'} (x)] d x .$

Đề thi liên quan

Câu hỏi mới nhất