Với giải Bài 2 trang 29 Chuyên đề Toán 11 Chân trời sáng tạo chi tiết trong Bài 5: Phép quay giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề Toán 11. Mời các bạn đón xem:
Giải Chuyên đề Toán 11 Bài 5: Phép quay
Bài 2 trang 29 Chuyên đề Toán 11: Cho hai tam giác đều ABC và AB’C’ như Hình 9. Gọi M, N lần lượt là trung điểm của BB’ và CC’. Chứng minh ∆AMN đều.
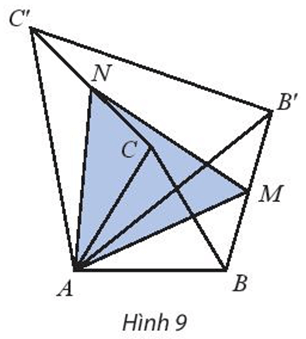
Lời giải:
Do DABC là tam giác đều nên AB = AC và
Do DAB’C’ là tam giác đều nên AB’ = AC’ và
Ta có phép quay tâm A, góc quay 60° biến:
⦁ Điểm B thành điểm C;
⦁ Điểm B’ thành điểm C’.
Do đó ảnh của đoạn thẳng BB’ qua phép quay tâm A, góc quay 60° là đoạn thẳng CC’.
Mà M, N lần lượt là trung điểm của BB’, CC’ (giả thiết).
Do đó phép quay tâm A, góc quay 60° biến điểm M thành điểm N.
Suy ra AM = AN và
DAMN có AM = AN và nên là tam giác đều.
Vậy ∆AMN đều.
Xem thêm lời giải bài tập Chuyên đề học tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Khởi động trang 25 Chuyên đề Toán 11: Vẽ mỗi hình sau ra một tờ giấy, cắt rời mỗi hình theo hình tròn. Tìm một điểm O trên mỗi hình. Sau đó, ghim hình đã cắt được xuống mặt bàn tại điểm O, thử xoay hình một góc φ nào đó. Có nhận xét gì về kích thước của hình trước khi xoay và sau khi xoay?...
Khám phá 1 trang 25 Chuyên đề Toán 11: a) Tìm phép biến hình biến ∆BAC thành ∆BA’C’ (Hình 1).....
Thực hành 1 trang 26 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, tìm tọa độ của các điểm là ảnh của điểm lần lượt qua các phép quay Q(O, 45°), Q(O, 90°), Q(O, 180°), Q(O, 360°)....
Vận dụng 1 trang 27 Chuyên đề Toán 11: Một con tàu đang di chuyển theo hướng bắc. Người lái tàu phải thực hiện phép quay nào trên bánh lái để con tàu:....
Khám phá 2 trang 27 Chuyên đề Toán 11: Cho phép quay Q(O; φ) và hai điểm tùy ý A, B (O, A, B không thẳng hàng) như Hình 6. Vẽ A’, B’ là ảnh của A, B qua phép quay. Hai tam giác OAB và OA’B’ có bằng nhau không?...
Thực hành 2 trang 28 Chuyên đề Toán 11: Cho hình vuông ABCD có cạnh bằng a và có tâm I, tìm ảnh qua phép quay Q(I, 90°) của các hình sau:....
Vận dụng 2 trang 28 Chuyên đề Toán 11: Kính lục phân là một dụng cụ quang học sử dụng gương quay để thực hiện phép quay Q(O, φ) biến tia Ox (song song với đường chân trời) thành tia Oy (song song với trục Trái Đất), nhờ đó đo được góc φ giữa trục của Trái Đất và đường chân trời tại vị trí của người đo. Hãy giải thích tại sao góc φ của phép quay này lại cho ta vĩ độ tại điểm sử dụng kính....
Bài 1 trang 28 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho các điểm A(–4; 2), B(–4; 5) và C(–1; 3)....
Bài 2 trang 29 Chuyên đề Toán 11: Cho hai tam giác đều ABC và AB’C’ như Hình 9. Gọi M, N lần lượt là trung điểm của BB’ và CC’. Chứng minh ∆AMN đều.....
Bài 3 trang 29 Chuyên đề Toán 11: Cho hình chữ nhật ABCD. Gọi E, F, H, K, L, I, J lần lượt là trung điểm của AB, BC, CD, DA, KF, HC, HL. Chứng minh hình thang AEJK và hình thang FLIC bằng nhau....
Bài 4 trang 29 Chuyên đề Toán 11: Chỉ ra phép quay có thể biến mỗi hình trong Hình 10 thành chính nó....
Bài 5 trang 29 Chuyên đề Toán 11: Cho hai tam giác vuông cân OAB và OA’B’ có chung đỉnh O sao cho O nằmtrên.n đoạn AB’ và nằm ngoài đoạn A’B. Gọi G và G’ lần lượt là trọng tâm của ∆OAA’ và ∆OBB’. Chứng minh rằng ∆OGG’ là tam giác vuông cân.....
Xem thêm các bài giải Chuyên đề học tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Phép đối xứng tâm
Bài 5: Phép quay
Bài 6: Phép vị tự
Bài 7: Phép đồng dạng
Bài tập cuối chuyên đề 1
Xem thêm các bài giải Chuyên đề học tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Chuyên đề 1: Phép biến hình phẳng
Chuyên đề 2: Lý thuyết đồ thị
Chuyên đề 3: Một số yếu tố vẽ kĩ thuật