a) Giả sử G là một đồ thị với n đỉnh và (n-1)(n-2)/2 + 2 cạnh. Sử dụng Định lí Ore

a) Giả sử G là một đồ thị với n đỉnh và (n-1)(n-2)/2 + 2 cạnh. Sử dụng Định lí Ore

Van Anh Ngày: 27-06-2023 Lớp 11

1.6 K

Với giải Bài 2.12 trang 45 Chuyên đề Toán 11 Kết nối tri thức chi tiết trong Bài 9: Đường đi Euler và đường đi Hamilton giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề Toán 11. Mời các bạn đón xem:

Giải Chuyên đề Toán 11 Bài 9: Đường đi Euler và đường đi Hamilton

Bài 2.12 trang 45 Chuyên đề Toán 11: a) Giả sử G là một đồ thị với n đỉnh và $\frac{(n - 1) (n - 2)}{2} + 2$ cạnh. Sử dụng Định lí Ore, hãy chứng minh G có một chu trình Hamilton.

b) Tìm một đồ thị với n đỉnh và $\frac{(n - 1) (n - 2)}{2} + 1$ cạnh mà không có chu trình Hamilton.

Lời giải:

a) Định lí Ore: Nếu G là một đồ thị có n đỉnh (n $\geq$ 3) và mỗi cặp đỉnh không kề nhau đều có tổng bậc không nhỏ hơn n thì G có một chu trình Hamilton.

Ta có lí thuyết: Giả sử G là đồ thị đơn gồm n đỉnh và m cạnh. Nếu m $\geq \frac{n^{2} - 3 n + 6}{2}$ thì G là đồ thị có chu trình Hamilton.

Áp dụng vào bài toán ta được điều phải chứng minh.

b) Ta có đồ thị sau có 5 đỉnh, 7 cạnh và đồ thị không có chu trình Hamilton.

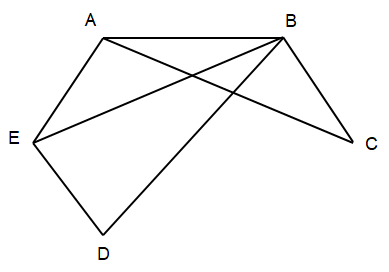
Chuyên đề Toán 11 Bài 9 (Kết nối tri thức): Đường đi Euler và đường đi Hamilton (ảnh 1)

Xem thêm lời giải bài tập Chuyên đề học tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Mở đầu trang 41 Chuyên đề Toán 11: Trong lí thuyết đồ thị, bài toán Bảy câu cầu ở Königsberg (nay là thành phố Kaliningrad, nước Nga) được phát biểu như sau: Thành phố có 7 cây cầu bắc qua sông như Hình 2.15a dưới đây, có thể nào đi dạo qua khắp các cây cầu nhưng mỗi cầu chỉ đi qua một lần không?...

HĐ1 trang 41 Chuyên đề Toán 11: Nhận biết đường đi Euler....

Luyện tập 1 trang 41 Chuyên đề Toán 11: Đồ thị nào dưới đây có một đường đi Euler? Hãy chỉ ra một đường đi Euler của nó....

HĐ2 trang 43 Chuyên đề Toán 11: Nhận biết đường đi Hamilton....

Luyện tập 2 trang 44 Chuyên đề Toán 11: Đồ thị nào trong Hình 2.2.3 có đường đi Hamilton? Hãy chỉ ra một đường đi Hamiton của nó....

Bài 2.7 trang 44 Chuyên đề Toán 11: Mỗi đồ thị sau có một chu trình Euler hoặc một chu trình Hamilton hay không? Hãy vẽ một chu trình Euler hoặc một chu trình Hamilton khi có thể.....

Bài 2.8 trang 44 Chuyên đề Toán 11: Có thể nào đi dạo chơi qua các cây cầu trong Hình 2.25, mỗi cây cầu vừa đúng một lần?...

Bài 2.9 trang 44 Chuyên đề Toán 11: Cho đồ thị G như Hình 2.26. Tìm một chu trình Hamilton xuất phát từ đỉnh S của G.....

Bài 2.10 trang 44 Chuyên đề Toán 11: Cho đồ thị G như Hình 27. Tìm một đường đi Hamilton từ S đến R....

Bài 2.11 trang 45 Chuyên đề Toán 11: Hãy chỉ ra một ví dụ chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G không nhỏ hơn $\frac{n}{2}$ trong Định lí Dirac, không thể thay bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn $\frac{n - 1}{2}$ ”....

Bài 2.12 trang 45 Chuyên đề Toán 11: a) Giả sử G là một đồ thị với n đỉnh và $\frac{(n - 1) (n - 2)}{2} + 2$ cạnh. Sử dụng Định lí Ore, hãy chứng minh G có một chu trình Hamilton....

Bài 2.13 trang 45 Chuyên đề Toán 11: Với giá trị nào của n thì đồ thị đầy đủ K_n có một chu trình Euler? Có một đường đi Euler?...

Bài 2.14 trang 45 Chuyên đề Toán 11: Với giá trị nào của n thì đồ thị đầy đủ K_n có một chu trình Hamilton? Có một đường đi Hamilton?...

Xem thêm các bài giải chuyên đề học tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 8: Một vài khái niệm cơ bản

Bài 9: Đường đi Euler và đường đi Hamilton

Bài 10: Bài toán tìm đường tối ưu trong một vài trường hợp đơn giản

Bài tập cuối chuyên đề 2

Bài 11: Hình chiếu vuông góc và hình chiếu trục đo

Xem thêm các bài giải chuyên đề học tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Chuyên đề 1: Phép biến hình trong mặt phẳng

Chuyên đề 2: Làm quen với một vài khái niệm của lí thuyết đồ thị

Chuyên đề 3: Một số yếu tố vẽ kĩ thuật

Từ khóa :

Toán 11

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Chứng minh rằng biểu thức sau luôn luôn dương với mọi x, y: B = x^2 - 2x + y^2 + 4y + 6

Chứng minh rằng biểu thức sau luôn luôn dương với mọi x, y: B = x^2 - 2x + y^2 + 4y + 6 Lữ Ngọc My My

55

Toán Tổng hợp kiến thức

3/(1^2.2^2 ) + 5/(2^2.3^2 ) + 7/(3^2.4^2 ) + ... + 19/(9^2.10^2). Chứng minh nhỏ hơn 1

3/(1^2.2^2 ) + 5/(2^2.3^2 ) + 7/(3^2.4^2 ) + ... + 19/(9^2.10^2). Chứng minh nhỏ hơn 1 Lữ Ngọc My My

52

Toán Tổng hợp kiến thức

Tính tổng: 1/4 + 1/12 + 1/24 + 1/40 + 1/60 + 1/84

Tính tổng: 1/4 + 1/12 + 1/24 + 1/40 + 1/60 + 1/84 Lữ Ngọc My My

42

Toán Tổng hợp kiến thức

Tìm x; y nguyên 2xy + 2x - y = 8

Tìm x; y nguyên 2xy + 2x - y = 8 Lữ Ngọc My My

43

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.