Với tóm tắt lý thuyết Toán lớp 8 Bài 1: Phân thức đại số sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 8.
Lý thuyết Toán lớp 8 Bài 1: Phân thức đại số
A. Lý thuyết Phân thức đại số
1. Khái niệm
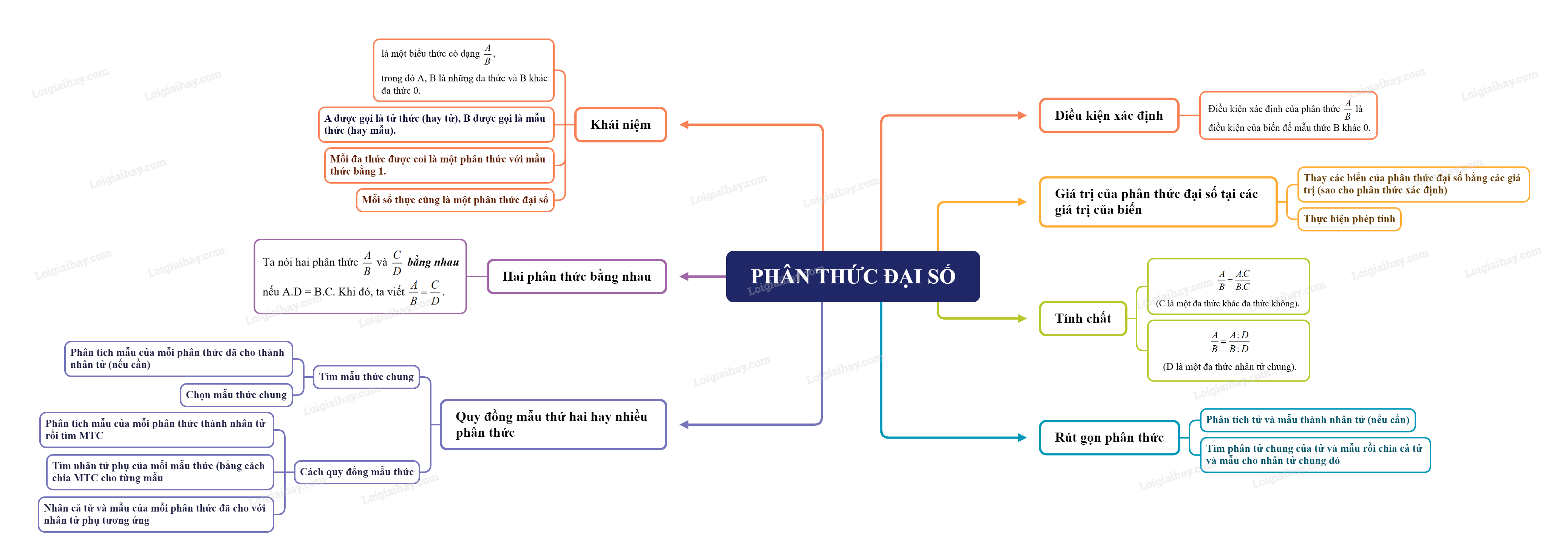
Một phân thức đại số (hay còn gọi là phân thức) là một biểu thức có dạng , trong đó P, Q là những đa thức và Q khác đa thức 0.
P được gọi là tử thức (hay tử), Q được gọi là mẫu thức (hay mẫu).
Chú ý: Mỗi đa thức được coi là một phân thức với mẫu thức bằng 1. Đặc biệt, mỗi số thực cũng là một phân thức đại số.
Ví dụ: là các phân thức đại số.
không phải là phân thức vì không phải là đa thức.
Hai phân thức bằng nhau
Ta nói hai phân thức và bằng nhau
nếu A.D = B.C. Khi đó, ta viết .
Ví dụ: Hai phân thức và bằng nhau.
2. Tính chất
Khi nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.
(C là một đa thức khác đa thức không).
Khi chia cả tử và mẫu của một phân thức cho cùng một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho.
(D là một đa thức nhân tử chung).
Ví dụ: Để biến đổi phân thức thành , ta chia cả tử và mẫu của phân thức cho y – x, khi đó
3. Rút gọn phân thức
Muốn rút gọn một phân thức, ta có thể làm như sau:
Bước 1. Phân tích tử và mẫu thành nhân tử (nếu cần)
Bước 2. Tìm nhân tử chung của tử và mẫu rồi chia cả tử và mẫu cho nhân tử chung đó.
Ví dụ:
4. Quy đồng mẫu thức của nhiều phân thức
Mẫu thức chung (MTC) chia hết cho mẫu thức của mỗi phân thức đã cho.
Tìm mẫu thức chung:
Bước 1. Phân tích mẫu của mỗi phân thức đã cho thành nhân tử (nếu cần)
Bước 2. Chọn mẫu thức chung.
Quy đồng mẫu thức hai hay nhiều phân thức:
Bước 1. Phân tích mẫu của mỗi phân thức thành nhân tử rồi tìm MTC
Bước 2. Tìm nhân tử phụ của mỗi mẫu thức (bằng cách chia MTC cho từng mẫu
Bước 3. Nhân cả tử và mẫu của mỗi phân thức đã cho với nhân tử phụ tương ứng
Ví dụ: Quy đồng mẫu thức hai phân thức và
MTC là:
Ta có:
Khi đó:
5. Điều kiện xác định, giá trị của phân thức đại số
Xác định điều kiện xác định của phân thức
Điều kiện xác định của phân thức là điều kiện của biến để mẫu thức B khác 0.
Giá trị của phân thức đại số
Cho phân thức đại số . Giá trị của biểu thức tại những giá trị cho trước của các biến để giá trị của mẫu thức khác 0 được gọi là giá trị của phân thức tại những giá trị cho trước của biến đó.
Ví dụ: Phân thức P = xác định khi hay
Tại x = 3,
Sơ đồ tư duy Phân thức đại số.
B. Bài tập Phân thức đại số
Bài 1. Rút gọn phân thức sau:
a) ;
b) .
Hướng dẫn giải
a) ;
b)
Bài 2. Quy đồng mẫu thức các phân thức trong mỗi trường hợp sau:
a) và ;
b) và .
Hướng dẫn giải
a) Ta có MTC là: (x + 2y)(x – 2y) .
;
.
b) Ta có: x2 – 16 = (x – 4)(x + 4) .
Chọn MTC là (x – 4)(x + 4).
; .
Bài 3. Viết điều kiện xác định của mỗi phân thức sau:
a) ;
b) ;
c) ;
d) .
Hướng dẫn giải
a) Điều kiện xác định của phân thức là 5x + 5 ≠ 0 hay 5x ≠ −5 hay x ≠ −1 .
b) Điều kiện xác định của phân thức là: y2 + 4 ≠ 0 (luôn đúng vì y2 + 4 > 0 với mọi y).
c) Điều kiện xác định của phân thức là: x + 1 ≠ 0 hay x ≠ −1.
d) Điều kiện xác định của phân thức là x – y ≠ 0 hay x ≠ y.
Video bài giảng Toán 8 Bài 1: Phân thức đại số - Cánh diều
Xem thêm các bài tóm tắt Lý thuyết Toán lớp 8 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 4: Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử
Lý thuyết Bài 1: Phân thức đại số
Lý thuyết Bài 2: Phép cộng, phép trừ phân thức đại số
Lý thuyết Bài 3: Phép nhân, phép chia phân thức đại số
Lý thuyết Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số