Với tóm tắt lý thuyết Toán lớp 11 Bài 5: Hình lăng trụ và hình hộp sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 11.
Lý thuyết Toán lớp 11 Bài 5: Hình lăng trụ và hình hộp
A. Lý thuyết Hình lăng trụ và hình hộp
I. Hình lăng trụ
1. Định nghĩa
- Hình gồm hai đa giác , và các tứ giác ,,…, được gọi là hình lăng trụ và kí hiệu là .
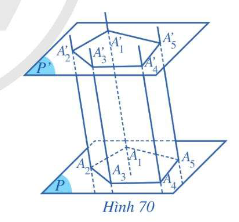
- Trong hình lăng trụ
+ Các điểm và được gọi là các đỉnh.
+ Các đoạn thẳng được gọi là các cạnh bên, các đoạn thẳng.và gọi là cạnh đáy của hình trụ.
+ Hai đa giác và được gọi là hai mặt đáy của hình lăng trụ.
+ Các tứ giác ,,…, gọi là các mặt bên của hình trụ.
* Chú ý: Nếu đáy của lăng trụ là một tam giác, tứ giác, ngũ giác,… thì lăng trụ tương ứng gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác.
2. Tính chất
- Các cạnh bên của hình lăng trụ song song và bằng nhau.
- Các mặt bên của hình lăng trụ là các hình bình hành.
- Hai mặt đáy của hình lăng trụ là hai đa giác có các cạnh tương ứng song song và bằng nhau.
II. Hình hộp
1. Định nghĩa
- Hình hộp là hình lăng trụ có đáy là hình bình hành.
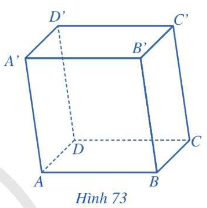
- Trong mỗi hình hộp, ta gọi:
+ Hai mặt không có đỉnh chung là hai mặt đối diện.
+ Hai cạnh song song không nằm trong một mặt phẳng là hai cạnh đối diện.
+ Hai đỉnh không thuộc cùng một mặt là hai đỉnh đối diện.
+ Đoạn thẳng nối hai đỉnh đối diện là đường chéo.
2. Tính chất
- Các mặt của hình hộp là hình bình hành.
- Hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau.
Sơ đồ tư duy Hình lăng trụ và hình hộp.
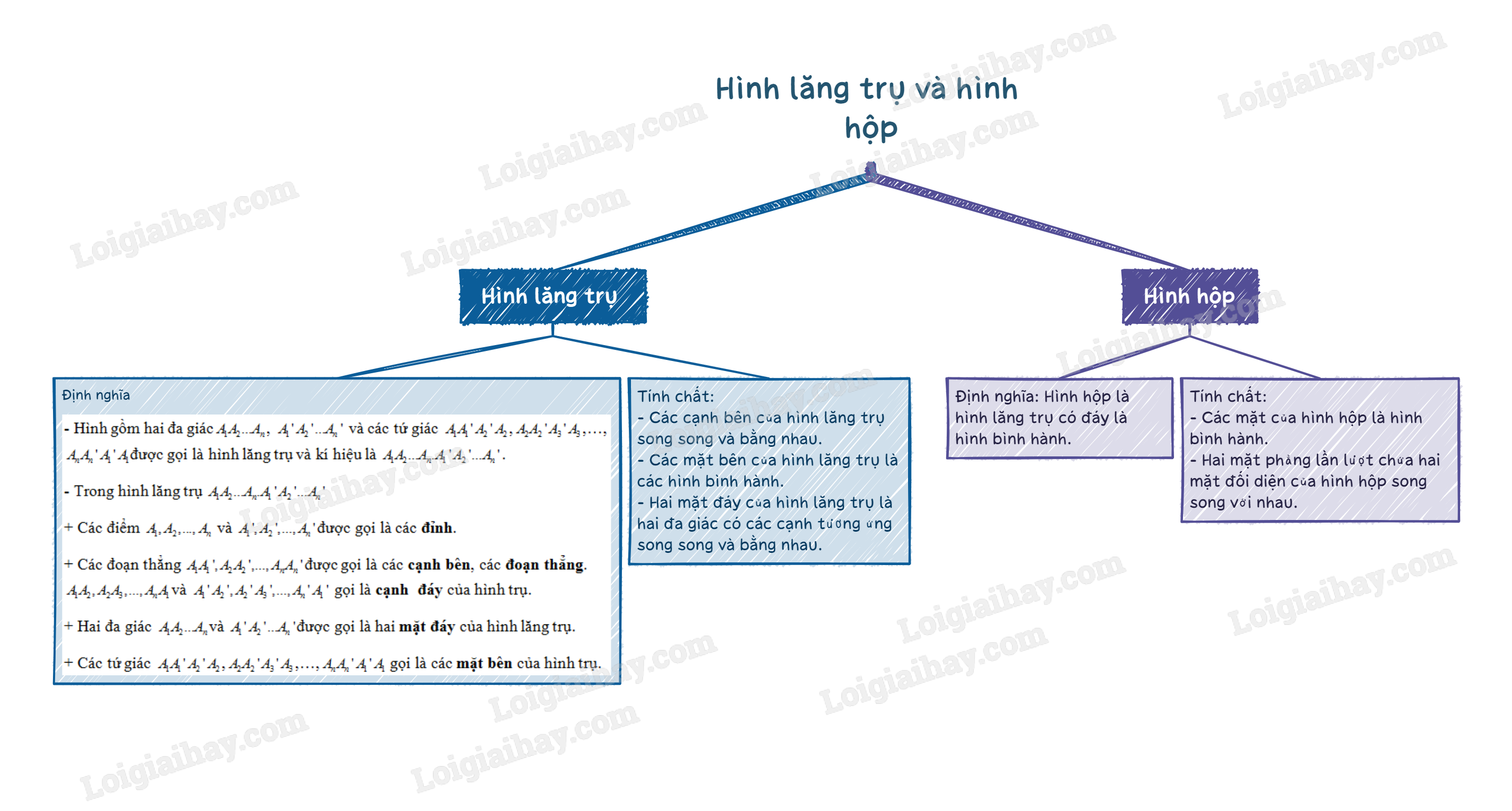
B. Bài tập Hình lăng trụ và hình hộp
Bài 1. Cho hình lăng trụ ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của các cạnh AB, A’B’. Chứng minh:
a) Tứ giác MNC’C là hình bình hành.
b) (B’MC) // (ANC’).
Hướng dẫn giải
a) Hình bình hành ABB’A’ có: M, N là trung điểm AB, A’B’.
Suy ra MN là đường trung bình của hình bình hành ABB’A’.
Do đó MN // BB’ và MN = BB’.
Mà BB’ // CC’ và BB’ = CC’ (do tứ giác BCC’B’ là hình bình hành).
Suy ra MN // CC’ và MN = CC’.
Vậy tứ giác MNC’C là hình bình hành.
b) Ta có ABB’A’ là hình bình hành.
Suy ra A’B’ // AB và A’B’ = AB.
Mà M, N lần lượt là trung điểm của AB, A’B’.
Do đó B’N // AM và B’N = AM.
Vì vậy tứ giác AMB’N là hình bình hành.
Khi đó AN // B’M.
Suy ra AN // (B’MC) (1)
Ta có tứ giác MNC’C là hình bình hành, suy ra NC’ // MC.
Do đó NC’ // (B’MC) (2)
Trong (ANC’) có N = AN ∩ NC’ (3)
Từ (1), (2), (3), ta thu được (ANC’) // (B’MC).
Bài 2. Cho hình hộp ABCD.A’B’C’D’. Gọi M là trung điểm AB và N là giao điểm của A’D và AD’.
a) Xác định giao tuyến d của hai mặt phẳng (CMN) và (ADD’A’).
b) Gọi F, G lần lượt là giao điểm của đường thẳng d với các đường thẳng AA’ và DD’. Chứng minh MF // CG.
Hướng dẫn giải
a) Trong (ABCD): gọi E = CM ∩ AD.
Mà CM ⊂ (CMN) và AD ⊂ (ADD’A’).
Suy ra E đều thuộc (CMN) và (ADD’A’) (1)
Lại có N là giao điểm của AD’ và A’D (giả thiết).
Suy ra N nằm trên mặt phẳng (ADD’A’).
Do đó N đều thuộc (CMN) và (ADD’A’) (2)
Từ (1), (2), ta thu được NE là giao tuyến của (CMN) và (ADD’A’) hay d ≡ NE.
b) Ta có M ∈ AB (giả thiết).
Mà AB ⊂ (ABB’A’), suy ra M ∈ (ABB’A’).
Lại có M ∈ (CMN) nên M đều thuộc (CMN) và (ABB’A’) (3)
Ta có F ∈ NE và F ∈ AA’.
Mà NE ⊂ (CMN) và AA’ ⊂ (ABB’A’).
Suy ra F đều thuộc hai mặt phẳng (CMN) và (ABB’A’) (4)
Từ (3), (4), suy ra MF là giao tuyến của (CMN) và (ABB’A’).
Chứng minh tương tự, ta được CG là giao tuyến của (CMN) và (CDD’C).
Ta có (ABB’A’) // (CDD’C) (tính chất hình hộp).
Mà (CMN) ∩ (ABB’A’) = MF và (CMN) ∩ (CDD’C) = CG.
Vậy MF // CG.
Bài 3. Cho hình lăng trụ ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của các cạnh BB’, CC’.
a) Xác định giao tuyến d của hai mặt phẳng (AMN) và (A’B’C’).
b) Chứng minh d // (ABC).
Hướng dẫn giải
a) Trong (AA’C’C): gọi D = A’C’ ∩ AN.
Mà A’C’ ⊂ (A’B’C’) và AN ⊂ (AMN).
Suy ra D đều thuộc hai mặt phẳng (AMN) và (A’B’C’) (1)
Trong (AA’B’B): gọi E = AM ∩ A’B’.
Mà AM ⊂ (AMN) và A’B’ ⊂ (A’B’C’).
Suy ra E đều thuộc hai mặt phẳng (AMN) và (A’B’C’) (2)
Từ (1), (2), suy ra DE là giao tuyến của hai mặt phẳng (AMN) và (A’B’C’) hay d ≡ DE.
b) Hình bình hành BCC’B’, có: M, N lần lượt là trung điểm của BB’, CC’.
Suy ra MN là đường trung bình của hình bình hành BCC’B’.
Do đó MN // B’C’ // BC.
Ta có:
⦁ MN = (AMN) ∩ (MNC’B’);
⦁ B’C’ = (A’B’C’) ∩ (MNC’B’);
⦁ DE = (AMN) ∩ (A’B’C’);
⦁ MN // B’C’ (chứng minh trên).
Suy ra DE // MN // B’C’.
Mà B’C’ // BC (chứng minh trên).
Do đó DE // BC.
Mà BC ⊂ (ABC).
Vậy DE // (ABC) hay d // (ABC).
Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 4: Hai mặt phẳng song song
Lý thuyết Bài 5: Hình lăng trụ và hình hộp
Lý thuyết Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian
Xem thêm các bài tóm tắt lý thuyết chương Toán lớp 11 Cánh diều hay, chi tiết khác:
Lý thuyết Chương 1: Hàm số lượng giác và phương trình lượng giác
Lý thuyết Chương 2: Dãy số. Cấp số cộng. Cấp số nhân
Lý thuyết Chương 3: Giới hạn. Hàm số liên tục
Lý thuyết Chương 4: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song